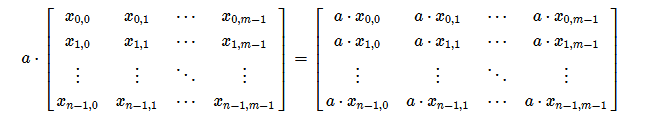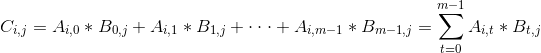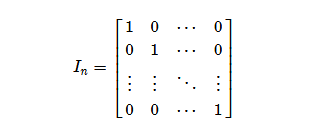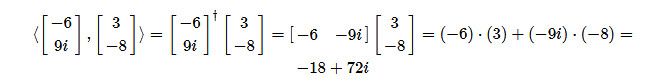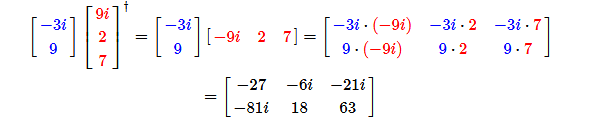量子计算基础02-线性代数
目录
第一部分：矩阵和基本运算
第二部分：高级操作
第三部分：特征值与特征向量
- 线性代数导论
线性代数是专门研究矩阵和向量性质的数学分支，在量子计算中广泛应用于表示量子态及其运算。这里只包含线性代数的基础知识，帮助大家了解线性代数在量子计算中的应用。
如果不了解复数，建议先阅读上一篇关于复数的博客，以便更好学习线性代数的相关知识。
后面练习用的是Python内置的复数模块（cmath），下面介绍一下cmath的一些特殊语法：
1、z代表复数，实部则为z.real，虚部为z.imag
2、将j放在实数之后来表示虚数，如3.14j
3、一个实数加一个虚数表示复数
4、abs可以计算虚数的模
在学习之前，导入必要的库和定义矩阵：
from typing import List
import math
import cmath
Matrix = List[List[complex]]第一部分：矩阵和基本运算
- 矩阵和向量
矩阵是排列在一个矩形网格中的数字，比如 
，是一个2*2的矩阵。
表示矩阵A的第i行第j列的元素，如
。
一个n * m的矩阵有n行和m列，形式如下图：
量子计算使用复数矩阵：矩阵的元素可以是复数，比如 
是有效的复数矩阵。
一个向量是n * 1的矩阵，如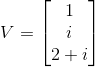 
就是一个3*1的向量。因为向量的宽度固定为1，所以可以只用一个索引来表示向量元素。如 
。
-
矩阵加法
使用列表来表示矩阵的话，每个子列表都是一行，[[1, 2], [3, 4]]表示
。
使用Python定义矩阵加法：
输入：
1.一个n * m的矩阵A，表现为一个二维列表
2.一个n * m的矩阵B，表现为一个二维列表
目标：
返回矩阵A与B的和，一个n * m的矩阵，表现为一个二维列表
# 创建全0矩阵
def create_empty_matrix(n: int, m:int) -> Matrix:
re = []
for i in range(n):
tmp = []
for j in range(m):
tmp.append(0)
re.append(tmp)
return re
# 矩阵加法
def matrix_add(a: Matrix, b:Matrix) -> Matrix:
# 获取矩阵大小
n = len(a)
m = len(b)
# 创建n * m的全0矩阵
ans = create_empty_matrix(n, m)
# 计算矩阵元素值
for i in range(n):
for j in range(m):
x = a[i][j]
y = b[i][j]
ans[i][j] = x + y
return ans
- 标量乘法
标量乘法就是将整个矩阵乘以一个标量（实数或复数），如下图，a为标量：
标量乘法有以下特性：
使用Python定义标量乘法：
输入：
1.一个标量x
2.一个n * m的矩阵A
目标：
返回x * A，一个n * m的矩阵
# 标量乘法
def scalar_mult(x: complex, a: Matrix) -> Matrix:
n = len(a)
m = len(a[0])
# 创建n * m的全0矩阵
ans = create_empty_matrix(n, m)
# 计算矩阵元素值
for i in range(n):
for j in range(m):
ans[i][j] = x * a[i][j]
return ans
- 矩阵乘法
矩阵乘法是一个非常重要但又很不寻常的算法。不寻常之处在于，它的操作数和输出大小都不相同：一个n * m的矩阵乘以一个m *k的矩阵得到一个n * k的矩阵。也就是说，要使矩阵乘法使用，第一个矩阵的列数必须等于第二个矩阵的行数。比如C=A*B的公式描述：
通过下面简例理解下上面公式：
矩阵乘法有如下性质：
，其中x为标量
注意：矩阵乘法是不可交换的，AB很少等于BA。
矩阵乘法的另一个重要性质是，一个矩阵乘以一个向量会得到另一个向量。
下图是一个特殊的单位矩阵
，主对角线上是1，其他地方都是0。它的特殊之处在于，如果是一个m * n的矩阵，那么任意矩阵A（大小n * m），存在 
。所以又被称为单位矩阵，作为一个乘法单元，它与数字1是等价的。
使用Python定义矩阵乘法：
输入：
1.一个n * m的矩阵A
2.一个m * k的矩阵B
目标：
返回矩阵AB,一个n * k的矩阵
# 矩阵乘法
def matrix_mult(a: Matrix, b: Matrix) -> Matrix:
# 获取输出矩阵大小
n = len(a)
m = len(b[0])
# 创建n * m全0矩阵
ans = create_empty_matrix(n, m)
# 计算矩阵元素值
for i in range(n):
for j in range(len(b[0])):
tmp = 0
for k in range(len(b)):
tmp += a[i][k] * b[k][j]
ans[i][j] = tmp
return ans
- 逆矩阵
一个n * n的矩阵A，如果满足 
，那么A是可逆的，
称为A的逆矩阵。
然后对于兼容大小的B和C，我们会发现一些有趣的事情：
一个方阵有一个叫做行列式的性质，矩阵A的行列式写成|A|，必须是方阵（n * n）才有行列式。
对于一个2 * 2的矩阵，行列式的定义是：
对于一个n阶矩阵，只有当
，才可逆。这里介绍一个二阶矩阵求逆公式：
使用Python定义二阶矩阵求逆
输入：
1.一个2 * 2的矩阵A
目标：
返回A的可逆矩阵
# 二阶矩阵求逆
def matrix_inverse(a: Matrix) -> Matrix:
# 获取矩阵元素
det_a = a[0][0] * a[1][1] - a[0][1] * a[1][0]
if det_a == 0:
print("A don't have inverse matrix")
return
# 创建全0矩阵
n = len(a)
ans = create_empty_matrix(n, n)
# 获取元素
g = a[0][0]
h = a[0][1]
i = a[1][0]
j = a[1][1]
# 计算逆矩阵，根据公式
ans[0][0] = j / (g*j - h*i)
ans[0][1] = (-h) / (g*j - h*i)
ans[1][0] = (-i) / (g*j - h*i)
ans[1][1] = g / (g*j - h*i)
return ans
- 转置运算
转置运算记作
，本质是矩阵在对角线上的反射，即 
。n * m的矩阵A，它的转置矩阵，大小为m * n，如下图：
对称矩阵是一个方阵，它是自身的转置：
。换句话说，它在主对角线上具有反射对称性（因此得名），例如，这个矩阵是对称的： 
矩阵乘积的转置等于矩阵转置后的乘积，按相反的顺序取： 
用Python定义矩阵的转置：
输入：
1.一个n * m的矩阵A
目标：
返回m * n的转置矩阵
# 转置矩阵
def transpose(a: Matrix) -> Matrix:
n = len(a)
m = len(a[0])
# 创建全0矩阵
ans = create_empty_matrix(m, n)
# 给转置矩阵赋值
for i in range(n):
for j in range(m):
ans[j][i] = a[i][j]
return ans- 共轭
下面要介绍的是矩阵共轭，取矩阵中的每一个元素的复共轭，如下图：
有个特性需要记住，矩阵的乘积的共轭，等于矩阵共轭的乘积： 
使用Python定义矩阵共轭：
输入：
1.一个n * m的矩阵A
目标：
返回A的共轭矩阵，n * m的
# 矩阵共轭
def conjugate(a: Matrix) -> Matrix:
n = len(a)
m = len(a[0])
# 创建全0矩阵
ans = create_empty_matrix(n, m)
for i in range(n):
for j in range(m):
ans[i][j] = complex(a[i][j].real, -a[i][j].imag)
return ans
- 伴随矩阵
最后一个单矩阵算法是转置和共轭的结合，称为矩阵A的伴随矩阵： 
如果一个矩阵等于它的伴随矩阵，我们称其为厄米矩阵： 
，例如 
矩阵乘积的伴随可以进行这样的转换： 
使用Python定义伴随矩阵
输入：
1.一个n * m的矩阵A
目标：
返回A的伴随矩阵
，大小为m * n
# 矩阵伴随
def adjoint(a: Matrix) -> Matrix:
# 矩阵转置
tmp = transpose(a)
# 矩阵共轭
ans = conjugate(tmp)
return ans-
酉矩阵
酉矩阵对于量子计算非常重要，当一个矩阵A可逆时，它是酉的，它的逆等于它的伴随： 
只有当一个n * n的方阵满足 
时，它是可酉的。例如：
使用Python判断一个矩阵是否为酉矩阵
输入：
1.一个n * m的矩阵A
目标：
判断这个矩阵是否为酉矩阵，输出为True或False
tip：在计算机上使用float时会有误差（舍入误差），Python中又一个approx函数，可以用来检查2个数字是否足够接近。
# 判断矩阵是否酉矩阵
from pytest import approx
def is_matrix_unitary(a: Matrix) -> bool:
# 如果非方阵，则不是酉矩阵
if len(a) != len(a[0]):
return False
# a的伴随矩阵
tmp_adj = adjoint(a)
print(tmp_adj)
# a乘以它的伴随矩阵
tmp_re = matrix_mult(a, tmp_adj)
print(tmp_re)
# 判断结果是否为单位矩阵，如果不是返回False
for i in range(len(tmp_re)):
for j in range(len(tmp_re[0])):
if i == j:
if approx(tmp_re[i][j]) != 1:
return False
elif approx(tmp_re[i][j]) != 0:
return False
return True
- 小结
经过第一部分的学习，已经掌握了足够的线性代数知识，能够开始学习量子位元的概念和单量子门的内容。下面将继续学习更高级的矩阵运算，这些内容有助于理解量子位元和量子门的性质。
第二部分：高级操作
- 内积
内积是另一个重要的矩阵运算，它仅适用于向量。给定两个相同大小的向量V和W，他们的内积 
:
我们把这个过程分解下便于理解，一个1 * n的矩阵（一个n * 1的向量的伴随矩阵）乘以一个n * 1的向量，结果是一个1 * 1的矩阵（它等价于一个标量），内积的结果就是这个标量。换句话说，计算两个向量的内积，取对应的元素 
和 
，然后将 的共轭复数乘以 ，再将这些乘积相加：
举个简单的例子：
内积具有以下特性：
（一个向量乘以一个酉矩阵，与向量自己的内积相同）
使用Python定义内积
输入：
1.一个n * 1的向量V
2.一个n * 1的向量W
目标：
返回一个复数 - 内积
# 内积
def inner_prod(v: Matrix, w: Matrix) -> complex:
# 求v的伴随矩阵
v_adj = adjoint(v)
# 求内积
ans = matrix_mult(v_adj, w)
# 内积是非负实数，虚部为0，所以取结果的实部
ans = ans[0][0].real
return ans-
向量范数
内积的一个直接作用就是计算向量范数，定义是 
，这将向量压缩成一个非负的实数。如果向量表示空间中的坐标，则范数恰好是向量长度。如果一个向量的模等于1，那么它就被称为标准化向量。
使用Python定义向量归一化：
输入：
1.一个非0的n * 1的向量
目标：
返回V的向量归一化结果，一个n * 1的向量
# 向量归一化
def normalize(v : Matrix) -> Matrix:
# 求内积
tmp_vvip = inner_prod(v, v)
# 求的开方
tmp_vvip_sqrt = math.sqrt(tmp_vvip.real)
# 求归一化向量
ans = scalar_mult((1 / tmp_vvip_sqrt), v)
return ans
- 外积
两个向量V和W，他们的外积定义为 
。也就是说，一个n * 1的向量和一个m * 1的向量的外积是一个n * m的矩阵。如果我们用X来代表V和W的外积，那么 
。下图是一个简单的例子：
用Python定义外积
输入：
1.一个n * 1的向量V
2.一个m * 1的向量W
目标：
返回V和W的外积，一个n * m的矩阵X
# 外积
def outer_prod(v: Matrix, w:Matrix) -> Matrix:
# 求w的伴随
w_adj = adjoint(w)
# 求外积
ans = matrix_mult(v, w_adj)
return ans
- 张量积
张量积是矩阵相乘的另一种方式。张量积不是用行乘以列，而是用第二矩阵乘以第一矩阵的每个元素。
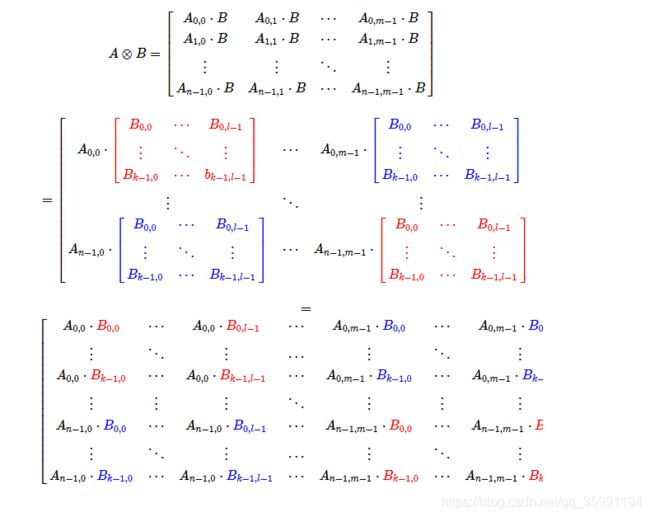
对于n * m的矩阵A和k * l的矩阵B，他们的张量积表示为 
，是一个 
的矩阵，如下图：
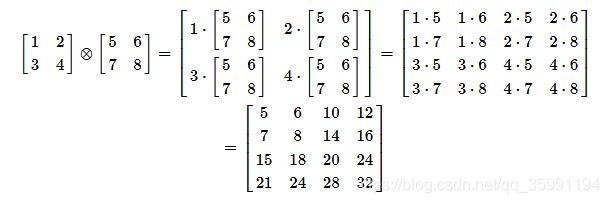
举一个简答的实例便于理解：
注意：两个向量的张量积还是一个向量，比如n * 1的向量V和m * 1的向量W， 
是一个 
的向量。
张量积有如下性质：
用Python定义张量积：
输入：
1.n * m的矩阵A
2.k * l的矩阵B
目标：
返回A和B的张量积 ，一个 
的矩阵
# 张量积
def tensor_product(a: Matrix, b:Matrix) -> Matrix:
n = len(a)
m = len(a[0])
k = len(b)
l = len(b[0])
# 创建全0矩阵
ans = create_empty_matrix(n*k, m*l)
# 计算张量积每个元素值
for a_i in range(n):
for a_j in range(m):
for b_i in range(k):
for b_j in range(l):
ans[a_i * k + b_i][a_j * l +b_j] = a[a_i][a_j] * b[b_i][b_j]
return ans
- 小结
经过第二部分的学习，已经掌握了足够的知识去学习关于量子比特、但量子门、多量子比特系统和多量子比特门的概念。下一部分是对特征值和特征向量的简单介绍，它们用于量子计算中的更高级的内容。
第三部分：特征值与特征向量
先看一个例子，下面是一个矩阵和向量的乘积：
仔细观察下上面的示例，结果向量只是初始向量乘以一个标量，在上面的例子中是4。
一个非零的n * n的矩阵A，一个非零向量V，一个标量x，如果 
，那么x是A的一个特征值，V是A对于x的一个特征向量。
特征值和特征向量的性质在量子计算中有广泛的应用。
用Python定义寻找特征值
输入：
1.一个n * n的向量A
2.一个A的特征向量V
目标：
返回一个实数，A对于V的一个特征值
# 已知特征向量求特征值
def find_eigenvalue(a: Matrix, v: Matrix) -> float:
# 求av
tmp_vec = matrix_mult(a, v)
for i in range(len(tmp_vec)):
# 避免除0
if tmp_vec[i][0] != 0:
ev = tmp_vec[i][0] / v[i][0]
return ev
print("There is no eigenvalue")用Python定义已知二阶方阵特征值求特征变量
输入：
1.一个2*2的矩阵A
2.A的一个特征值x
目标：
返回任何与x相关的A的非零特征向量
推导过程：
, 
TIP：一个矩阵和一个特征值将有多个特征向量（实际上是无穷多个），通过上面的推导可以得到特征向量的两个元素之间的对应关系，给定其中一个元素一个确定的值，就可以得到另一个元素，注意除0风险。
# 已知特征值求特征向量(二阶)
def find_eigenvector(a: Matrix, x: float) -> Matrix:
# 创建空白向量
ans = create_empty_matrix(2, 1)
# 给特征向量第一个元素赋值
ans[0][0] = 1
# 判断分母是否为0
if a[0][1] != 0:
ans[1][0] = (x - a[0][0]) / a[0][1]
return ans
elif (x - a[1][1]) != 0:
ans[1][0] = a[1][0] / (x - a[1][1])
return ans
else:
print("There is no eigenvector")