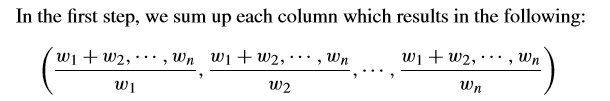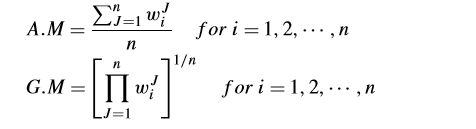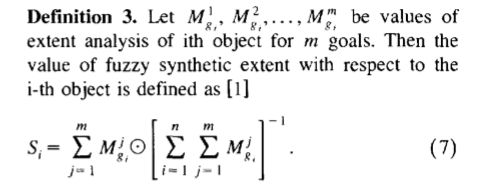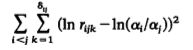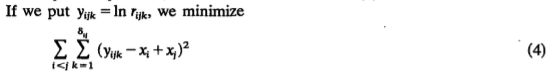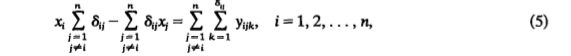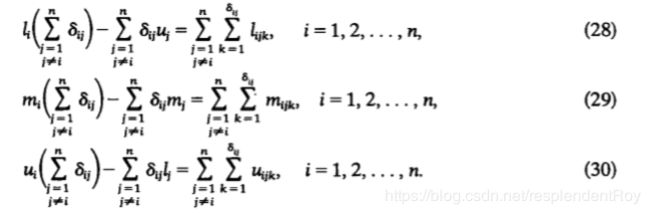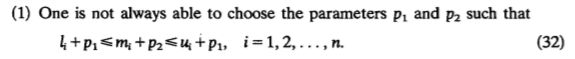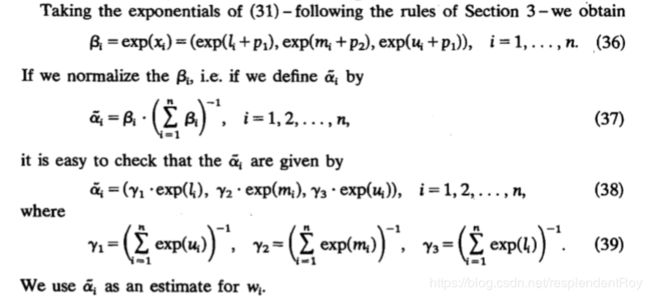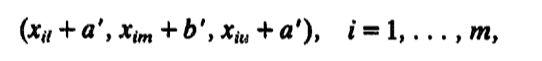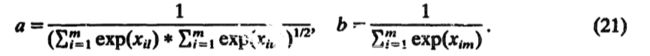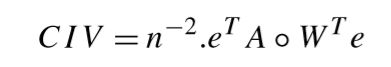Fuzzy analytic hierarchy process(模糊层次分析法)论文学习
论文:Fuzzy Analytic Hierarchy Process: A performance analysis of various algorithms(查题目了才知道原来Fuzzy是模糊的意思哈哈哈哈对8起
<一>那么什么是FAHP和AHP呢?
该类方法对于量化评价指标,选择最优方案提供了依据。(原来是决策相关方法
AHP存在如下方面的缺陷:检验判断矩阵是否一致非常困难,且检验判断矩阵是否具有一致性的标准CR < 0. 1缺乏科学依据;判断矩阵的一致性与人类思维的一致性有显著差异。
模糊层次分析法的基本思想和步骤与AHP的步骤基本一致,但仍有以下两方面的不同点:
(1)建立的判断矩阵不同:在AHP中是通过元素的两两比较建立判断一致矩阵;而在FAHP中通过元素两两比较建立模糊一致判断矩阵,实质上是由确切数衡量元素之间的关系变成模糊数来衡量
(2)求矩阵中各元素的相对重要性的权重的方法不同
AHP过程详解:
(1)层次模型:最顶层是我们的优化目标,中间层是判断候选方物或人优劣的因素或标准,最下面是候选方案。下图为最简单的三层结构,影响因素只有一层,也有多级多层次的影响因素,例如一级指标、影响一级指标的二级指标等。
![]()
是下层的因素影响上层,所以每一分支中下层的权重和加起来等于上层的权重和。
(2)判断矩阵
判断矩阵是衡量两两元素之间相对关系的矩阵,元素的物理意义是横排元素相对竖排元素的重要程度,用1-9来衡量
![]()
上图说半天也就是1-9依次重要性大大递增的关系,另外倒数关系使得判断矩阵满足正互反矩阵的要求。
1.从主观到客观 最后会殊途同归(因为都要满足一致性检验)但是仍然不能保证完全没有主观因素
2.判断矩阵是针对每一层次的 也就是每一个层次都有一个判断矩阵 只要你是同一层次的不同指标 就有一个判断矩阵 这样侧能一层一层地把权重分下去 同样要满足一致性检验的要求
(3)一致性检验
一致性矩阵定义:
![]()
只要判断矩阵满足一致性矩阵的定义,那么判断矩阵的权重分配就是成功的。
但是大部分判断矩阵显然不满足一致性(“画直角三角形”计算原则,要求挺高的,用几何形式去定义,就是先确定一个ij点,再在第j行上选一个点(jk),再从这个点(jk)往第i行做投影即可),但是一致性检验只需要满足CR=(CI/RI)<0.1即可。
(4)权重向量
![]()
一旦满足一致性,则权重向量则为最大特征值对应的特征向量归一化之后的结果。
FAHP过程详解:
如文章开头所述,FAHP与AHP本质的区别是AHP用确切数(crisp number)衡量元素之间的关系,FAHP用模糊数(fuzzy number)衡量元素之间的关系!而至于元素之间的关系是乘性还是加性,这个不是FAHP和AHP的本质区别。由此,下面这篇文章在定义上是有错误的。之前误导了我,也误导了大家,还好找老师问清楚了,希望之前看到这篇文章的朋友能再看一眼我的更新,不要被误导。https://wiki.mbalib.com/wiki/%E6%A8%A1%E7%B3%8A%E5%B1%82%E6%AC%A1%E5%88%86%E6%9E%90%E6%B3%95
除了上述区别之外,其他流程在总线上都是一样的,什么判断矩阵啊、一致性检测啊、由判断矩阵求最终的权重向量啊,只是在计算方法上有不同。毕竟FAHP是由AHP来的嘛。
<二>论文详解来了,正式进入FAHP
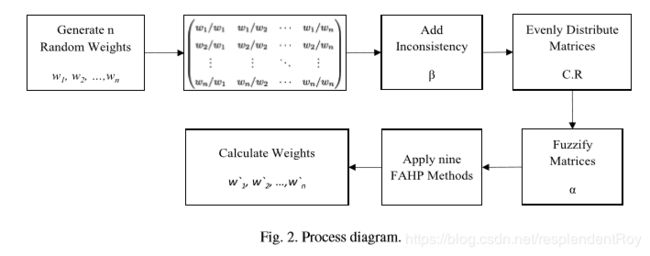
写这篇文章的是一个来自土耳其某大学的大好人,把FAHP方法常用的不常用的都凑一块儿(最早的论文是1983的古董论文,各位朋友应该还没出生呢吧,也是没谁了),其中常用的呢,五种,鉴于论文已经长达十九页,再加页就丧尽天良了,就没有再bb,只是把不常用的剩下四种简单介绍了下。接下来就进入实验环节了,当然前期要告诉你我这个实验流程。最开始生成准备材料,也就是要拿来被计算的这个判断矩阵(由标准答案增加模糊度和不一致性而来,标准答案就是完全一致的判断矩阵)以及它的标准答案,准备好了就直接扔进算法里面在不同条件下折腾出结果就好了。这个实验是典型的控制变量法(有仨变量:矩阵大小,模糊度,一致性),也就是对比试验,呜呜呜,想起来了被高中生物支配的恐惧。通过实验选拔出俩表现优秀的尖子生,一个叫modified LLSM,一个叫FICSM。惊了其实,因为这俩平时都挺默默无闻的 ,大家最喜欢拿来搞事儿的FEA反而在这次试验中表现不佳。但是毕竟FEA流量最大,不得不提下,你要用也行,最好把模糊度搞高点再用效果好些,苦口婆心和卑卑微微,哈哈哈哈哈。
好了,论文主要就是上面我说的这一大堆,接下来我从两个部分详细介绍下伪重点内容(嘻嘻,其实就是我组会要讲的内容,先打个草稿,别打我):九种方法各自都是怎么一回事,这次实验到底分出来个什么高低
(1)九种方法各自都是怎么一回事:
第一部分讲过哈,FAHP的大致流程,无非就是生成判断矩阵,由判断矩阵计算权重向量,根据权重拍板作决定。第一步放在“这次实验到底分出来个什么高低”来讲;第三步我们目前不考虑哈。也就是我们着重来看是怎么由判断矩阵计算权重向量的哈。
当然,不是所有的判断矩阵都能拿来计算权重向量,而是满足一定一致性的才可以。而且,我们就把这个在实际中满足一定一致性的判断矩阵当成完全一致性矩阵,那么,由完全一致性矩阵去计算权重向量的方法就是咱们的计算方法。ok,有了这个指导思想,相当于定了起点和目的地,至于你怎么过去,那么就开始八仙过海,各显神通了。
文章中只介绍了四种不常用的,先来看看这四种。
我们的起点是完全一致性矩阵,也即:
终点是权重向量,也即:(W1,W2,...,Wn)。
2.1.1 几何平均和算术平均(介个算两种了 FAM和FGM
(1)求列和,如下:
由于权重和为1,则可变形为:
(2)比较矩阵每个元素除以附属列的列和,可得:
观察所得矩阵,我们发现每一列的向量都相同,而且都是我们要求的答案。那么在实际中,由于并非完全一致,因此只是接近这种理想情况,那么实际情况下如何求得权重向量呢?一个合理的方法,就是求均值。一个为算术平均(aruthmetic mean),一个为几何平均(geometric mean),计算方法如下:
2.1.2 行求和 FRSM
FRSM是在FEA的基础上修改的,著名算法FEA分为两个部分:
第一步:求行和以及归一化
第二步:去模糊化(根据模糊数比较原则进行权重排名)
FRSM在第二步去模糊化时使用了基于质心来判断的原则。
2.1.3 列求和的逆 FICSM
前面我们求过列和,有:
再一看,列和向量的逆不就是我们朝思暮想的答案吗?
效果好的一些神来之笔人类不能理解,这是大自然对我们至今保留的秘密。我瞎比比啥呢哈哈。
好的,这四种的参观到此结束,让我们来看看最火的五种。
2.1.4 FEA
FEA是1996年中国人提出来的,被广泛应用,虽然方法上有缺陷,但是还是感觉很爽哈哈。废话少说,下面来看:
(1)为便于理解,我们从后往前看,从目的地往起点倒着走,矩阵W(14)就是我们要求的答案:
那么怎么求的呢?顺序是(12)->(13)->(14)
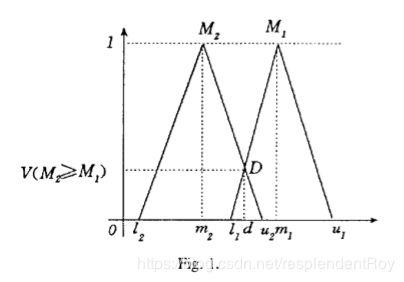
(2)往回倒,(12)中出现两个未知的东西,分别是(9)和(7)
(9):
PS:(9)中的函数分别从算术和几何角度解释一下:
(7):
PS:(7)中的M需要解释一下,M就是衡量指标之间关系的模糊数:
2.1.5 FEA with modified normalization
讲真,按照论文指路的那篇讲修正FEA的文章里面就是从方方面面批判了FEA哪哪哪儿不行,没有改进之处啊。
2.1.6 LLSM
谁都不能想到这样一个古董论文(1983)还这么难找,说实话,确实奠定了不少基础,毕竟模糊数的计算法则的提出既方便了大家,又是开天辟地式的。LLSM可能是这些方法里面最复杂的一种,但是还好效果不错,不然可能会早就被打死。
由于是盘古开天地式的,所以从priority theory讲起,再介绍模糊数的计算法则,并且一一证明!最后将priority theory推广到模糊数。当然咯,还是要举个例子演算下,就是后来大家都说好用的教授选拔经典案例(首先各个标准之间的优先级算好,然后再算每个候选人在各个子标准下的权重大小),反正FEA也用了。
(1)priority theory
所谓priority theory,也就是拟合完全一致矩阵的过程,对,思想和前面四种就不一样,是典型的数学思路,我要靠算出来的那种。用函数去衡量当前矩阵和完全一致矩阵之前的差距,求最小即可。就是下面这个关键的式子啦(和机器学习里面的代价函数是一个意思啵):
当然这里的![]() 是一定满足的,古往今来都是这样滴。
是一定满足的,古往今来都是这样滴。
但是对每一个标准,都可能有多个专家去评估,因此,对应的,每个rij也是有多个的。这个数就用![]() ij来表征。于是代价函数就变成如下形式,把每个rij都要拿来算一算:
ij来表征。于是代价函数就变成如下形式,把每个rij都要拿来算一算:
式子出来了,下面就是将数学问题进行到底,用经典的x,y来表示已知与未知。如下:
最后解最小值(笔者猜一猜,应该不外乎求导啥的)得到下面的等式:
到这里完全只剩下演算xi了,优先级理论到此结束。
(2)模糊数运算法则
1)加法:
2)乘法:
3)求逆:
4)取对数:
5)指数化:
(3)fuzzy priority theory
推广到模糊数,只有运算方式上发生了变化,思想上共用一个。
因此(5)式的代价函数还是代价函数,只不过变成模糊数而已。那么由带模糊数的(5)式求最小得到的式子就变成了仨:
我们要求的是(li,mi,ui),已知的是(lijk,mijk,uijk),也即多个专家对所有标准的评估结果再取对的结果,其中![]() ij就是参与评估的专家的人数。最后算出来结果就好了,结果如下:
ij就是参与评估的专家的人数。最后算出来结果就好了,结果如下:
其实到这也就基本结束了,但是大佬就是大佬,总是能想到别人想不到的东西,作者提示了两点,虽然两点我都没太看懂:
1.貌似是不需要保证最后结果模糊数的基本原则?
2.第二点的确是个特殊情况,我们知道,(28)--(30)的右边其实都是等于0的,至于为什么,且看分析如下:
28--30式子中右边都说了,i是不等于j的,也就是说是对除了对角线元素以外的所有元素求和,那么我们又知道元素是关于对角线呈倒数关系的,记住这一点。那么,求和对象是元素取对之后的,对数相加,等于底数相乘,相乘为1,则再取对为0呗。
因此后来的计算结果都是在右边求和为0的基础上建立的,但是对于不满足相加为0的矩阵(可能某一元素有两个专家评估,而和它关于对角线对称的有仨专家评估,就没办法相抵消),怎么办呢?
就直接暴力解矩阵方程,就好了:
最后再归一化,指数化:
2.1.7 LLSM with modified normalization
在LLSM的基础上,当前方法在保证最佳性(optimality)和归一化同时实现的情况下,进一步计算出了权重中的常数取值。回顾一下,LLSM得到的结果是:
当前方法中也即(换了个写法,换汤不换药):
接下来就是不知所云的解答过程:
最后解出来的结果是:
2.1.8 GMM
(2)这次实验到底分出来个什么高低:
本次实验采用控制变量法,首先由完全一致矩阵生成不完全一致矩阵(模拟人工得到的矩阵),分别测试了在只改变比较矩阵大小、模糊度或者一致性的各种情况下,由这些生成的不完全一致矩阵通过这九种方法计算的效果。为更好地理解实验结果,我们首先来看实验结果的衡量标准。
2.2.1 实验分析
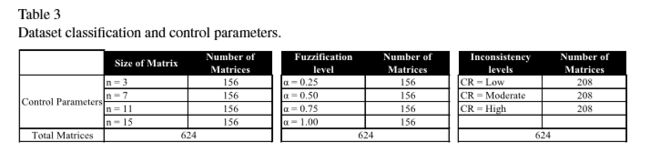
(1)准备数据,原本是生成了4X4X6X40(4种矩阵大小,4种阿尔法取值,6种贝塔取值(注意贝塔取值并不能衡量一致性))个矩阵的,但是由于这些矩阵的一致性分布情况并不均匀,于是后来从3840个矩阵中挑选出640(4X4X3)个矩阵,保证了三个变量下的不同取值的矩阵数量是分布均匀的。
(2)对模糊矩阵的一致性衡量(CR标准),本次实验是在模糊化之前衡量一致性的。一致性衡量标准如下:
(3)实验效果的衡量标准,由于我们的标准答案是起先就知道的,因此我们衡量算法效果就是比较计算结果与标准答案之间的的差距,本实验定义相容性指标(compatibility index value)来衡量算法性能。下面式子中的A是标准答案,W是计算结果。如果计算结果和标准答一模一样,那么CIV等于1,否则就是大于1。也就是说这个指标越小越好。实验中由于多次重复试验,因此计算的是mean CIV。
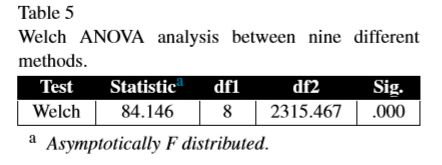
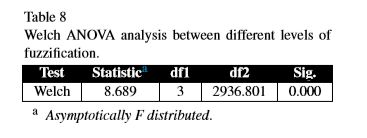
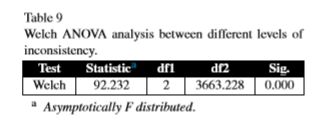
(4)为验证实验可行性(九种方法之间存在差异),最开始本来准备采用ANOVA(analysis od variance),也即方差分析法滴,但是由于数据是不满足方差一致性的,所以就改成了welch-ANOVA。
(5)为证明不同算法的实验结果(也即mean CIV)是有显著差异的,本实验采用了post hoc test,并用heat map、box-plots的方式展示mean CIV之间的区别有多大。
post hoc test:
heat map(所谓热图,就是用颜色突出大小关系及其程度,例如绿色系的就是前者小于后者,红色系的就是前者大于后者,程度越深则颜色越深):
box-plots:
2.2.2 实验流程
2.2.2.1 生成不完全一致矩阵流程以及伪代码:
下面我们详细来看下重点步骤:
(1)添加非一致性的过程
 在一个用元素本身和贝塔计算出来的区间里面任意挑选一个数去替换原来的元素。
在一个用元素本身和贝塔计算出来的区间里面任意挑选一个数去替换原来的元素。
(2)矩阵模糊化
也就是在阿尔法的帮助下,由一个数整出三个数。
2.2.2.2 矩阵大小为变量
(1)首先用welch-ANOVA坐实矩阵大小作为变量实验的可行性。
(2)分别在不用的矩阵大小条件下对九种算法进行计算,得到统计结果由箱型图展示,横坐标为矩阵大小,纵坐标为mean CIV:
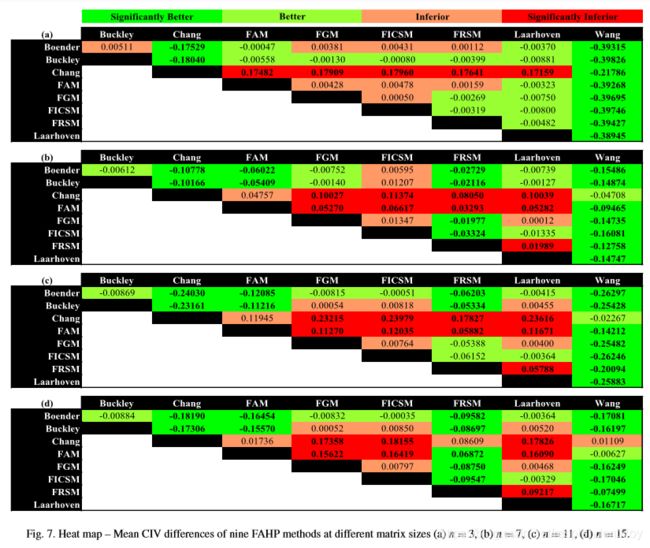
(3)对于每种算法,矩阵大小两两之间比较的heat map如下:
由于有四种规格的矩阵,于是对于每种方法,均有六次比较。
(4)对于每种大小,九种算法之间的比较的heat map如下:
2.2.2.3 模糊度为变量
(1)照例坐实模糊度作为变量分析的可行性
(2)分别在不用的模糊度条件下对九种算法进行计算,得到统计结果由箱型图展示,横坐标为矩阵大小,纵坐标为mean CIV:
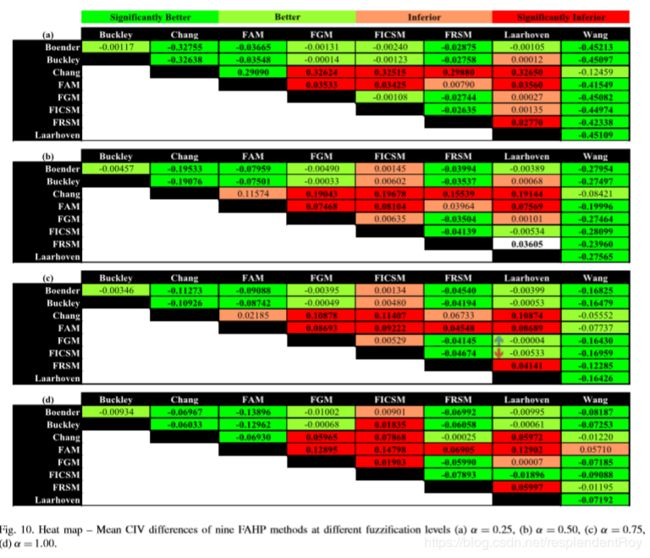
(3)对于每种算法,不同模糊度之间的比较的heat map如下:
(4)对于每种模糊度,九种算法之间的比较的heat map如下:
2.2.2.4 一致性为变量
(1)照例坐实一致性作为变量分析的可行性
(2)分别在不用的一致性条件下对九种算法进行计算,得到统计结果由箱型图展示,横坐标为矩阵大小,纵坐标为mean CIV:
(3)对于每种算法,不同一致性之间的比较的heat map如下:
(4)对于每种一致性,九种算法之间的比较的heat map如下:
2.2.3 实验结果
<一>三种变量下测试结果
(1)矩阵大小,结论如下:
1)大部分算法遵循矩阵越小,mean CIV越小,也即效果越好。只有FEA除外。
2)n=3时,GMM表现最好;n=7时,FICSM表现最好;n=11时和n=15时,均为LLSM with modified normalization表现最好。
(2)模糊度
1)只有FEA在模糊度上升的时候表现更好,其余均相反。
2)![]() =0.25,LLSM with modified normalization表现最好;
=0.25,LLSM with modified normalization表现最好;![]() =0.5、0.75以及1.0时,均为FICSM表现最好
=0.5、0.75以及1.0时,均为FICSM表现最好
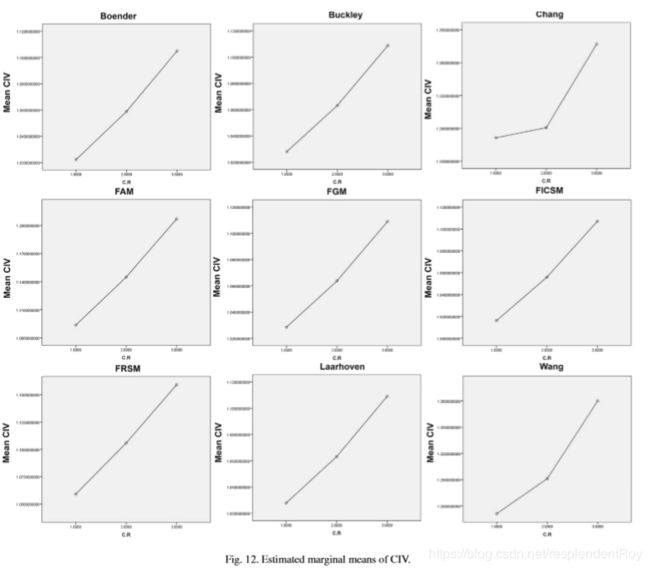
(3)一致性
1)所有算法均为一致性越高的时候表现越好
2)high inconsistency时,LLSM with modified normalization表现最好;其他情况均为FICSM表现最好
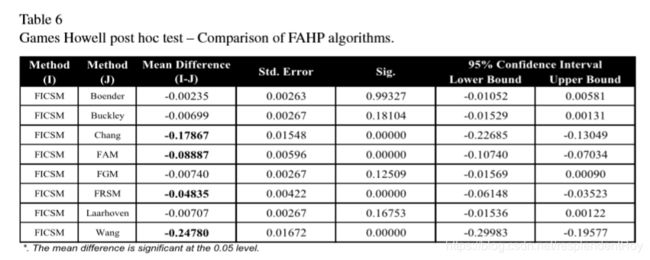
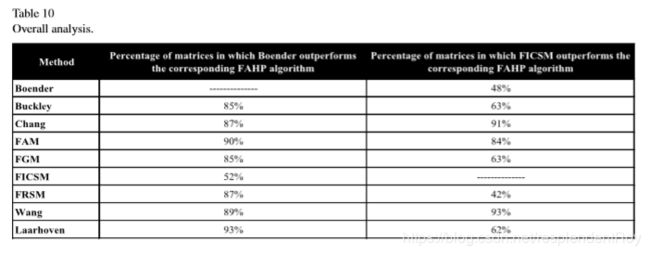
<二>单独拎俩尖子生再比一比
是不是发现FICSM和LLSM with modified normalization被表扬的次数最多,没错,作者又把这俩拎出来单独和其他方法(是的,只配叫做其他方法哈哈)做了比较,看看到底这俩尖子生有多虐。
最后作者苦口婆心地说,FEA虽然流量大,但实则不太行,要是你们非要用FEA的话,建议在提高模糊度的情况下使用效果更佳。
未完待续,稍后更新!有什么错误之处,欢迎批评指正,唉,估计没多少人能看到这里。