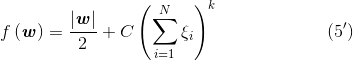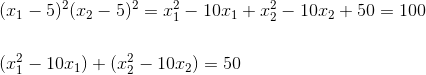数据挖掘笔记 - 支持向量机基础

参考文献

1. 《数据挖掘导论》 5.5支持向量机

一、支持向量机简介

本文中支持向量机的理论推导止于凸优化，至于是如何求解凸优化问题的请参阅其他文章。

1.支持向量机的基础概念

支持向量机（SVM）是利用最大边缘超平面对样本进行分类的方法，这里的边缘指的是和决策边界平行，到决策边界距离相等，且相交于最近的两类样本点的超平面之间的距离。边缘最大化的目的是为了最小化泛化误差。

在概率下，SVM分类器的泛化误差的上界满足：

，其中

其中是训练误差，是样本容量，是模型复杂度（复杂度越高，训练误差越小，与边缘负相关），根据上式可以得出：1）训练误差越大，泛化误差上确界越大；2）边缘越大，训练误差可能会更大，但是泛化误差的上界越小；3）概率越大，泛化误差上界越大（判断越肯定，内容信息量越少）；4）样本容量越大，可以降低模型复杂度和判断的肯定程度对泛化误差上界的正向影响（样本越多越好）。

SVM一般需要设定几个参数，包括：核函数，边缘软硬度（，）。

2.支持向量机的特点

1）SVM本质是一个凸优化问题，因此可以得到一个全局最优解。

2）SVM基础模型针对的是二元分类问题，但是可以通过嵌套实现解决多元分类问题。

 

二、线性支持向量机（完美可分）

设有一个样本容量为的样本集,其属性数据矩阵为，其标签向量为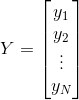，其中，表示第个样本的属性向量，那么一个线性分类器的决策边界可以写成如下形式：，即是一个线性流形（超平面）。下面以一个2维空间中的随机样本为例进行说明。

假设有两个样本点及处于决策边界上，那么可以得到如下等式：

于是可以得到。由于向量便是一个平行于决策边界的向量（起始点都在决策边界上），因此可以得出，向量和决策边界正交，如下图所示：

因此通过简单证明可以得到红色点满足，蓝色叉满足。如果红色点的类标号为1，而蓝色叉的类标号为-1，那么对于任何一个测试样本，可以进一步得到：

如上图所示，直线和分是线性分类器的边缘的边界线，离决策边界最近的两个样本点及分别在这两条直线上，在边界线上的点称为支持向量。假设：

注：这里是一个常数。直线和的斜率及截距是由向量和标量共同决定的，因此依然可以代表所有过点的直线，为了方便计算，可以设。

等式组（2）结合等式组（1）（其中），可以合并简化为：

等式组（2）中两式相减可得：

假设边界线沿着向量平行移动可以达到边界线，如果我们要计算分类器的边缘（宽度），那其实就是计算向量的模。由于向量和向量平行，因此向量就是向量在向量上的投影，于是根据向量内积（）的几何意义，可以得出：

结合等式（3）和等式（4），SVM问题可以归纳为一个凸优化问题，目标函数为

再加上约束，完整的优化问题如下：

这种模型下的SVM是没有训练误差的，既存在一个线性流形完美分割样本点，然而事实上这往往不太现实。

 

三、线性支持向量机（非完美可分）

现实中很少会出现完美可分的情况，因此一个标准的SVM应当考虑两个目标，第一是尽可能拓宽边缘，第二是 尽可能减少噪音进入甚至穿过边缘。因此需要引入一种称为软边缘的方法，即允许一定的训练误差。（事实上这种改良还能使线性SVM部分实现非线性可分）

在不等式（3）的基础上加入松弛变量，不等式（3）变为：

其中松弛变量是一个长度为的向量，当样本点所对应的不等式等号成立时，那么松弛变量是“紧的”，否则就是“松的”（类似凸优化中的互补松弛定理）。如图所示：

通过类似等式（4）的推导方法，可以得出直线（橙色）和直线（）的距离为。如上图所示，样本点所处的边界线是延向量方向平移得到的。此时不等式（3'）等号成立，即：

样本点突破了原来的边界线（甚至突破了原来的决策边界）。相比之下，样本点所处的边界线对应的不等式等号不成立且松弛变量（样本点和之前完美可分的情况一样），即：

因此可以看出，在加入软边缘的方法之后，可以通过松弛变量向量来度量SVM分类器的第二个目标：尽可能少的噪音进入甚至穿过边缘（尽可能少的训练误差），而向量中大于0的元素所对应的正是穿过边缘边界线的样本点，而且值越大，穿越程度越大，因此可以通过构造如下成本函数来度量训练误差：

其中简单线性地度量了噪音穿越边界造成的代价，和对代价分别进行了线性和几何的缩放，也就是说，参数和决定了软边缘的软硬度，当和中存在0时，边缘最软（可以不计成本的肆意穿越）。

因此目标函数由等式（5）改写为：

优化问题可以转换为：

 

四、非线性支持向量机（非线性变换）

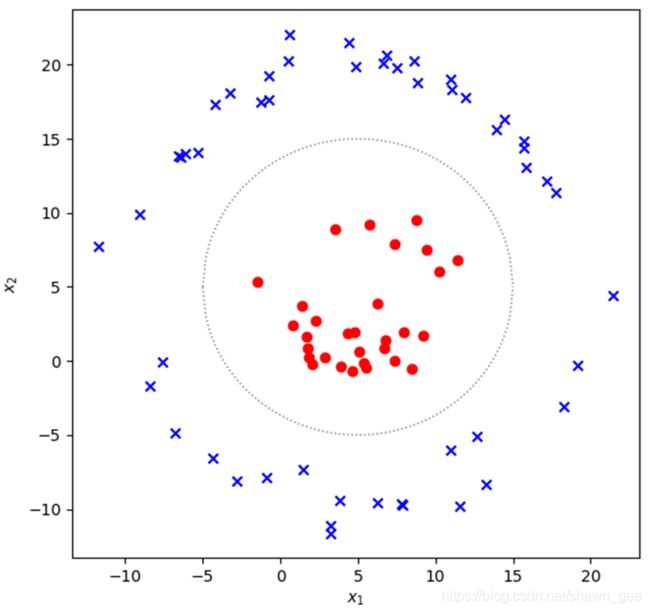
当遇到完全不可分的非线性情况时，如下图所示：

蓝色样本点就是在圆周围正态分布，而红色样本点则是在周围正态分布，因此最佳的决策边界是圆，也就是虚线的圆，这是一个非线性的决策边界。

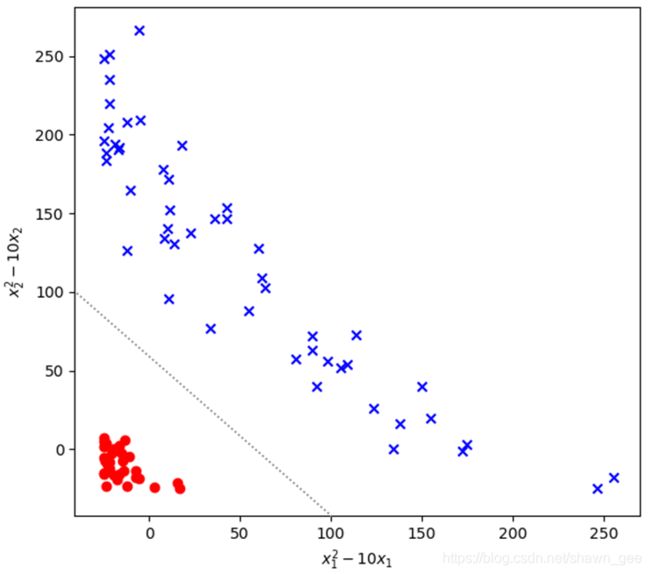
对决策边界进行简单计算，可以到如下等式：

从上面等式可以看到，决策边界是由和构成的一根直线。因此如果能把属性和进行非线性变换，变成由和表示的属性，那么就可以线性可分了，如下图所示：

其实为了方便展示，上面的例子已经对变换后的空间进行了降维（选取了新空间中两个维度的线性组合）。事实上如果要对数据矩阵进行非线性变换，会产生一个更高维的空间。以这个例子来讲，二维属性通过一个非线性变换（二次变换）转换到一个新的线性空间中（注：变换后还是个线性空间，而且决策边界也线性），即：

变换后取得了一个5维的高维数据，然后对这个高维数据使用高纬度的线性SVM分类器便可解决问题。非线性SVM的优化问题和线性SVM类似，只是需要对属性做一次非线性变换，进入高维空间中求解凸优化问题，即：

上个例子中（）决策边界的，。

事实上，这样会极大的浪费计算资源（2维数据变为5维数据），如果样本的属性本身维度较高，那么可能导致维灾难，比如一个1000维的属性数据矩阵，进行二次变换后会得到一个维度为的属性数据矩阵，从而需要使用一个50万维的线性SVM来进行分类，计算量大幅上升。

不过核函数技术可以解决上述问题，核函数在本质思想上依然是对原有数据进行升维，但是实际计算的时候是在原空间中进行的。

 

五、非线性支持向量机（核函数 Kernel Function）

依然考虑上面例子中的非线性变换，其中取什么值影响不大，这里是为了方便计算。假设有两样本和，那么进行非线性变换后，会得到两个处于新空间中的向量，，这两个向量的点积可以看做它们在变换后的空间中的相似程度：

通过上面等式的推导可以看出，原本需要在升维的新空间中进行的点积计算可以在更低维度的原空间中完成。上述等式可以记为函数：

这个在原空间（低维）中计算变换后空间（高维）的相似度的函数被称为核函数。当且仅当函数为正定核函数（满足Mercer定理）时，才能在在非线性SVM中使用（不确定对不对）。在实践中不需要了解变换的具体形式，可以直接使用函数。

Mercer定理（半懂不懂）：

核函数可以表示为：，当且仅当对于任意满足为有限值的函数，则，满足Mercer定理的核函数称为正定核函数（positive definite kernel function）（有的文章说是半正定函数）。