朴素贝叶斯文本分类算法
朴素贝叶斯文本分类算法
最近在学习推荐系统过程中,要用到朴素贝叶斯(Naïve Bayes)进行文本的分类。再一次深刻认识到学好基础知识的重要性,要理解朴素贝叶斯,需要有很好的概率与数理统计,离散数学基础。
一.Naive Bayes基础知识。
对于随机试验E有两个随机事件A,B,且P(B) > 0 那么在B事件发生的条件下A发生的概率为:
其中P(AB)为A,B两个事件的联合概率。对上式利用乘法公式可以变形为:
这样就得到了贝叶斯公式。贝叶斯文本分类就是基于这个公式,利用先验概率来得到文本的分类。
其中P(Ci)为第i个文本类别出现的概率,P(w1,w2…wn|Ci)为文本类别为Ci时出现特征向量(w1,w2…wn)的概率,P(w1,w2…wn)为特征向量出现的概率。一般的会假设特征——词,在文本中出现的概率是独立的,也就是说词和词之间是不相关的(虽然这个不一定成立,但是为了简化计算往往又不得不这么做),那么这时候的联合概率就可以表示为乘积的形式,如下: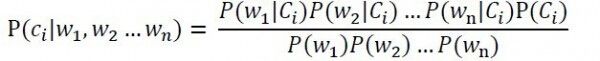
对于特定的训练集合来说,上式中P(w1)P(w2)…P(wn)是一个固定的常数,那么在进行分类计算的时候可以省略掉这个分母的计算,如是得到:
二.朴素贝叶斯的两种模型
朴素贝叶斯分类器是一种有监督学习,常见有两种模型。
1.多项式模型(multinomial model)即为词频型。
2.伯努利模型(Bernoulli model)即文档型。
二者的计算粒度不一样,多项式模型以单词为粒度,伯努利模型以文件为粒度,因此二者的先验概率和类条件概率的计算方法都不同。计算后验概率时,对于一个文档d,多项式模型中,只有在d中出现过的单词,才会参与后验概率计算,伯努利模型中,没有在d中出现,但是在全局单词表中出现的单词,也会参与计算,不过是作为“反方”参与的。
多项式模型和贝努利模型的关键区别:
1.贝努利模型是以“文档”为统计单位,即统计某个特征词出现在多少个文档当中(最大似然方法估计条件概率p(x(i)|c)的时候),当某个特征词在某一个文档中出现多次的时候,贝努利模型忽略了出现的次数,只算作一次。而多项式模型是以“词”为统计单位,当某个特征词在某个文档中多次出现的时候,与贝努利模型相反,它算作多次——这个更符合做NLP人的想法。
2.对特征向量中0值维度的处理。对于某个新的输入样本,当某个维度的取值是0的时候(也就是该特征词不出现在输入样本中),贝努利模型是要计算 p( x(i,0) | c(0)) 的值。而多项式模型直接忽略这样的特征,即只用 p( x(i,1) | c(0) )的值来进行计算,从而区分各个类别。
注意:朴素贝叶斯假设事物属性之间相互条件独立为前提。
三.多项式模型
1.基本原理
在多项式模型中,设某文档d=(t1,t2,…,tk),tk是该文档中出现过的单词,允许重复,则
先验概率P(c)=类c下单词总数/整个训练样本的单词总数
类条件概率P(tk|c)=(类c下单词tk在各个文档中出现过的次数之和+1)/(类c下单词总数+|V|)
V是训练样本的单词表(即抽取单词,单词出现多次,只算一个),|V|则表示训练样本包含多少种单词。 P(tk|c)可以看作是单词tk在证明d属于类c上提供了多大的证据,而P(c)则可以认为是类别c在整体上占多大比例(有多大可能性)。
2.举例
给定一组分好类的文本训练数据,如下: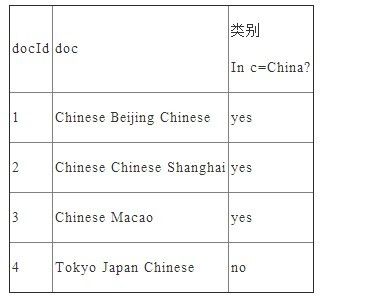
给定一个新样本Chinese ChineseChinese Tokyo Japan,对其进行分类。该文本用属性向量表示为d=(Chinese, Chinese, Chinese, Tokyo, Japan),类别集合为Y={yes, no}。
类yes下总共有8个单词(5个Chinese+1个Beijing+1个Shanghai+1个Macao),类no下总共有3个单词(1个Tokyo+1个Japan+1个Chinese),训练样本单词总数为11,因此P(yes)=8/11,P(no)=3/11。类条件概率计算如下:
//|V|表示训练样本包含多少种单词,即为:Chinese Beijing Shanghai Macao Tokyo Japan共6个
P(Chinese | yes)=(5+1)/(8+6)=6/14=3/7
P(Japan | yes)=P(Tokyo| yes)=(0+1)/(8+6)=1/14
P(Chinese|no)=(1+1)/(3+6)=2/9
P(Japan|no)=P(Tokyo| no)=(1+1)/(3+6)=2/9有了以上类条件概率,开始计算后验概率:分母中的8,是指yes类别下所有词出现的总数,也即训练样本的单词总数,6是指训练样本有Chinese,Beijing,Shanghai, Macao, Tokyo, Japan 共6个单词,3是指no类下共有3个单词。
P(yes | d)=P(Chinese|yes)×P(Japan|yes)×P(Tokyo|yes)*P(c)=(3/7)3×1/14×1/14×8/11=108/184877≈0.00058417
P(no | d)= P(Chinese|no)×P(Japan|no)×P(Tokyo|no)*P(c)=(2/9)3×2/9×2/9×3/11=32/216513≈0.00014780比较大小,即可知道这个文档属于类别china。
四.伯努利模型
1.基本原理
以文件为粒度,或者说是采用二项分布模型,伯努利实验即N次独立重复随机实验,只考虑事件发生/不发生,所以每个单词的表示变量是布尔型的类条件概率。
P(c)=类c下文件总数/整个训练样本的文件总数
P(tk|c)=(类c下包含单词tk的文件数+1)/(类c下文件总数+2)
备注:P(tk|c)中的(类c下文件总数+2)不是网上流传的(类c下单词总数+2)。
2.举例
继续以前面的例子为例,使用伯努利模型计算文本分类。
类yes下总共有3个文件,类no下有1个文件,训练样本文件总数为4,因此P(yes)=3/4, P(Chinese| yes)=(3+1)/(3+2)=4/5,条件概率如下:
//分子:Japan在yes分类中出现的文件数为0即0+1,分母:yes分类下文件总数为3,即3+2.
//Tokyo 同理
P(Japan | yes)=P(Tokyo| yes)=(0+1)/(3+2)=1/5
//分子:Beijing在yes分类中出现的文件数为1即1+1,分母:yes分类下文件总数为3,即3+2.
//Macao,Shanghai同理
P(Beijing | yes)= P(Macao|yes)= P(Shanghai|yes)=(1+1)/(3+2)=2/5
P(Chinese|no)=(1+1)/(1+2)=2/3
P(Japan|no)=P(Tokyo| no)=(1+1)/(1+2)=2/3
P(Beijing| no)= P(Macao| no)= P(Shanghai | no)=(0+1)/(1+2)=1/3P(yes|d)=P(yes)×P(Chinese|yes)×P(Japan|yes)×P(Tokyo|yes)×(1-P(Beijing|yes))×(1-P(Shanghai|yes))×(1-P(Macao|yes))=3/4×4/5×1/5×1/5×(1-2/5) ×(1-2/5)×(1-2/5)=81/15625≈0.005
P(no|d)= P(no)×P(Chinese|no)×P(Japan|no)×P(Tokyo|no)×(1-P(Beijing|no))×(1-P(Shanghai|no))×(1-P(Macao|no))=(1/4)×(2/3)×(2/3)×(2/3)×(1-1/3)×(1-1/3)×(1-1/3)=16/729≈0.022因此,这个文档不属于类别china。
相关内容链接:
原文链接:http://www.chepoo.com/naive-bayesian-text-classification-algorithm-to-learn.html