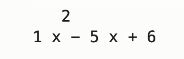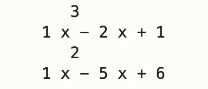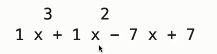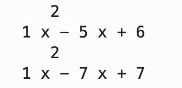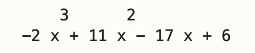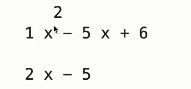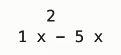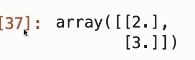Python数据分析 - 机器学习笔记：第一章数据分析 - 1.2.5多项式和线性方程组
前言：本文是学习网易微专业的《python全栈工程师》 中的《数据分析 - 机器学习工程师》专题的课程笔记，欢迎学习交流。
一、课程目标
- 创建多项式及其计算
- 掌握线性方程组的求解方法
二、详情解读
2.1.创建多项式及其计算
2.1.1.多项式
- 数学表示
f ( x ) = a 0 x n + a 1 x n − 1 + . . . + a n − 1 x + a n f(x) = a_0x^n + a_1x^{n-1}+ ... + a_{n-1}x + a_n f(x)=a0xn+a1xn−1+...+an−1x+an
↓ ↓ ↓ \downarrow\downarrow\downarrow ↓↓↓
[ a 0 , a 1 , . . . a n − 1 , a n ] [a_0, a_1, ... a_{n-1}, a_n] [a0,a1,...an−1,an]
1.创建多项式：
import numpy as np
# f(x) = x^3 - 2x + 1
# 这里从最高次幂的系数写起
# 相当于：f(x) = x^3 + 0x^2 -2x + 1
# 所以数组是[1, 0, -2, 1]
a = np.array([1, 0, -2, 1])
fx = np.poly1d(a) # 这里返回的是多项式对象
fx
运行结果：
type(fx)
fx(1)
运行结果：
print(fx)
创建表达式：g = (x - 1)^2 + 3(x-1) + 2
p = np.poly1d([1, 3, 3])
g = lambda x: p(x - 1)
g(0) # 等于0
g(1) # 等于2
运行结果： 为0
基于根创建多项式：
root = np.array([2, 3])
p2 = np.poly1d(root, r=True)
print(p2)
运行结果：
在显示上，更换变量：
a = np.array([1, 0, -2, 1])
p3 = np.poly1d(a, variable='k')
print(p3)
运行结果：
2.多项式运算：
a = np.array([1, 0, -2, 1])
fx = np.poly1d(a)
root = np.array([2, 3])
p2 = np.poly1d(root, r=True)
print(fx)
print(p2)
运行结果：
加法、减法运算：
print(fx + p2)
print(fx - p2)
运行结果：
乘法、除法运算：
print(fx * p2)
print(fx / p2)
运行结果：
上图中第一个数组是商，第二个数组是余数。
多项式运算，本质是系数运算，系数可以用数组、列表表示
加法：
p4 = p2 + [-2, 1]
print(p2)
print(p4)
运行结果：
乘法：
p5 = p2 * np.array([-2, 1])
print(p5)
运行结果：
除法：
p5 / [-2, 1]
运行结果：
微分：
pd = p2.deriv()
print(p2)
print(pd) # 求p2的微分
运行结果：
积分：
pint = pd.integ()
print(pint)
运行结果：
求多项式的根：
root = np.array([2, 3])
p2 = np.poly1d(root, r=True)
r = np.roots(p2)
print(p2)
print(r)
运行结果：
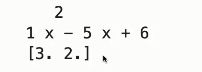
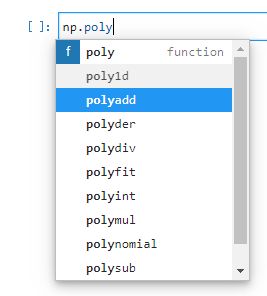
技巧：tab
当输入以下内容时，忘记函数的名字，按tab键
np.poly
会出现很多可选函数：
2.2.解线性方程组
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 . . . . . . a m 1 x 1 + a m 2 x 2 + . . . + a m n x n = b m a_{11}x_1 + a_{12}x_2+...+a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2+...+a_{2n}x_n = b_2 \\ ......\\ a_{m1}x_1 + a_{m2}x_2+...+a_{mn}x_n = b_m a11x1+a12x2+...+a1nxn=b1a21x1+a22x2+...+a2nxn=b2......am1x1+am2x2+...+amnxn=bm
为了求解上面的线性方程组，可以转化为矩阵方式，如下所示：
[ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n ⋮ ⋮ ⋮ ⋮ a m 1 a m 2 . . . a m n ] [ x 1 x 2 ⋮ x n ] = [ b 1 b 2 ⋮ b n ] \begin{bmatrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ a_{m1} & a_{m2} & ... & a_{mn} \\ \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n\\ \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \\ \end{bmatrix} ⎣⎢⎢⎢⎡a11a21⋮am1a12a22⋮am2......⋮...a1na2n⋮amn⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡x1x2⋮xn⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡b1b2⋮bn⎦⎥⎥⎥⎤
m = n时方程组有唯一确定的解
示例：
{ 3 x 0 + x 1 = 9 x 0 + 2 x 1 = 8 \begin{cases} 3x_0 + x_1 = 9 \\ x_0 + 2x_1 = 8 \end{cases} {3x0+x1=9x0+2x1=8
使用numpy.linalg.solve()求解
a = np.array([[3, 1], [1, 2]])
b = np.array([[9], [8]])
x = np.linalg.solve(a, b)
x
运行结果：
三、课程小结
- 01 多项式
- 02 求解线性方程组