ISLR系列：(4.3)模型选择 PCR & PLS

Linear Model Selection and Regularization

此博文是 An Introduction to Statistical Learning with Applications in R 的系列读书笔记，作为本人的一份学习总结，也希望和朋友们进行交流学习。

该书是The Elements of Statistical Learning 的R语言简明版，包含了对算法的简明介绍以及其R实现，最让我感兴趣的是算法的R语言实现。

  【转载时请注明来源】：http://www.cnblogs.com/runner-ljt/

   Ljt   勿忘初心  无畏未来

   作为一个初学者，水平有限，欢迎交流指正。

 

---

        前两小节介绍的模型选择方法，要么是选择全体自变量的一个合适子集，要么是使得某些自变量的回归系数收缩为0.这两种方法都是建立

在初始自变量集上，而本小节将要介绍的主成分分析（PCR）和偏最小二乘回归（PLS）是将初始自变量转化为新的变量进行回归的方法。

        PCR是一种非监督学习方法，能够有效的降低自变量的维数，消除多重共线性的影响。

        PLS是一种新型的多元统计数据分析方法，近十年来，它在理论、方法和应用方面都得到了迅速的发展。密西根大学的弗耐尔教授称偏最小

二乘回归为第二代回归分析方法。不同于PCR，PLS为一种监督式的学习方法，其目的是既找到能够解释自变量同时也能够解释因变量的方向。

偏最小二乘回归=多元线性回归分析+典型相关分析+主成分分析。

         PLS有以下优点：

         (1)PLS是一种多因变量对多自变量的回归建模方法

         (2)能够在自变量存在严重多重共线性的情况下进行回归建模

         (3)允许在样本量少于自变量个数的情况下进行建模

         (4)最终模型包含所有自变量，易于辨别系统信息和噪声，自变量的回归系数便于解释

 

---

  PCR  &  PLS

     pcr（formula,data,scale=F,validation = c("none", "CV", "LOO")）

      pls（formula,data,scale=F,validation = c("none", "CV", "LOO")）

      validation：验证方法   CV： 10折交叉验证  ； LOO ：留一验证

       输出结果：  CV score ： the root mean squared error  均方根误差/标准误差

                           the percentage of variance explained

      validationplot（object,val.type=c('RMSEP','MSEP','R2')） 验证统计量绘图函数

       object：mvr对象

       val.type=c('RMSEP','MSEP','R2'） :  RMSEP:预测均方根误差        ; MSEP:预测均方误差

 

      

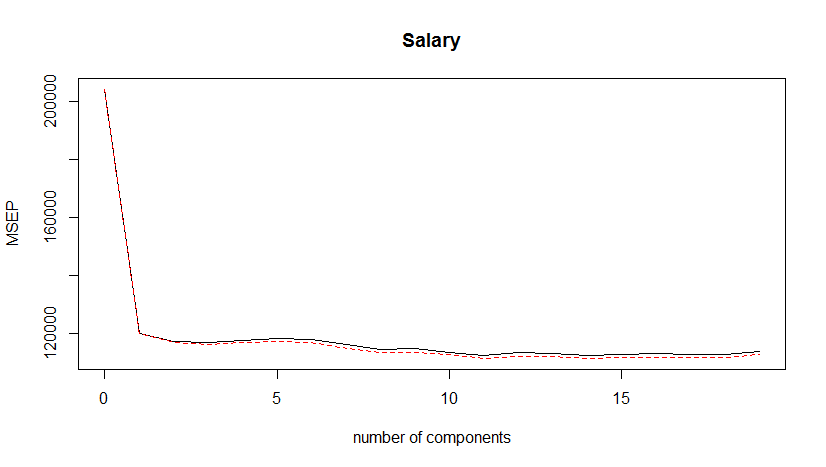
> library(ISLR)
> library(pls)
> set.seed(2)
> Hitters<-na.omit(Hitters)
> 
> pcr.fit<-pcr(Salary~.,data=Hitters,scale=T,validation='CV')
> summary(pcr.fit)
Data:     X dimension: 263 19 
    Y dimension: 263 1
Fit method: svdpc
Number of components considered: 19

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps
CV             452    348.9    352.2    353.5    352.8    350.1    349.1    349.6    350.9    352.9     353.8
adjCV          452    348.7    351.8    352.9    352.1    349.3    348.0    348.5    349.8    351.6     352.3
       11 comps  12 comps  13 comps  14 comps  15 comps  16 comps  17 comps  18 comps  19 comps
CV        355.0     356.2     363.5     355.2     357.4     347.6     350.1     349.2     352.6
adjCV     353.4     354.5     361.6     352.8     355.2     345.5     347.6     346.7     349.8

TRAINING: % variance explained
        1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps  11 comps  12 comps
X         38.31    60.16    70.84    79.03    84.29    88.63    92.26    94.96    96.28     97.26     97.98     98.65
Salary    40.63    41.58    42.17    43.22    44.90    46.48    46.69    46.75    46.86     47.76     47.82     47.85
        13 comps  14 comps  15 comps  16 comps  17 comps  18 comps  19 comps
X          99.15     99.47     99.75     99.89     99.97     99.99    100.00
Salary     48.10     50.40     50.55     53.01     53.85     54.61     54.61
> 
> validationplot(pcr.fit,val.type='MSEP')
> 
> 
> 
> set.seed(1)
> pls.fit<-plsr(Salary~.,data=Hitters,scale=T,validation='CV')
> summary(pls.fit)
Data:     X dimension: 263 19 
    Y dimension: 263 1
Fit method: kernelpls
Number of components considered: 19

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps  11 comps  12 comps
CV             452    346.7    342.3    341.9    343.3    344.2    343.6    340.9    338.4    338.9     337.2     335.5     336.8
adjCV          452    346.4    341.8    341.2    342.3    342.7    341.9    339.2    336.7    337.1     335.7     334.1     335.1
       13 comps  14 comps  15 comps  16 comps  17 comps  18 comps  19 comps
CV        336.5     335.7     336.1     336.2     336.1     335.9     337.6
adjCV     334.8     334.0     334.4     334.5     334.4     334.2     335.7

TRAINING: % variance explained
        1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps  11 comps  12 comps  13 comps
X         38.08    51.03    65.98    73.93    78.63    84.26    88.17    90.12    92.92     95.00     96.68     97.68     98.22
Salary    43.05    46.40    47.72    48.71    50.53    51.66    52.34    53.26    53.52     53.77     54.04     54.20     54.32
        14 comps  15 comps  16 comps  17 comps  18 comps  19 comps
X          98.55     98.98     99.24     99.71     99.99    100.00
Salary     54.47     54.54     54.59     54.61     54.61     54.61
> 
> validationplot(pls.fit,val.type='MSEP')

 

                     

      

                       

 

 

 

 

 

---

 

 

 

 

 

 

转载于:https://www.cnblogs.com/runner-ljt/p/4871399.html