量子推断（quantum inference）&Grover算法

综述

量子推断和Grover算法都隶属于量子搜索算法中的子类，其中，量子推断可以作为Grover算法的一种实际应用场景。在这之中使用到了一点点关于量子（quantum）的概念，Grover作为一个算法，很好地将量子quantum中的叠加态superposition原则应用到了计算机上，对于搜索具有极大的加速作用。本文只用到了一点点的量子的概念，所以一定能看懂的。

细节

量子quantum的叠加态

|ψ> = a|0> + b|1> (a²＋b²=1)
是量子中的基本假设，也是Grover算法应用的主要优点。
这等式的意思就是变量ψ既是0又是1，在没有进行测量measure之前，永远处于0和1的叠加状态。就像一只猫又生又死，一个人又男又女，这就是量子的独特魅力和优点。

Grover算法

Household矩阵

定义

A = I - 2αHα
α是单位向量
H代表共轭转置，在实数域中等价于转置，他和转置有共同的性质
I为单位矩阵

Household矩阵的数学意义

这个household矩阵在工程领域很常用，因为它有一个宝贵的性质：将一个向量除第一个元素以外的所以元素都化为零
这意味着任何的向量都可以由它变成（1,0,0,…0,0）这个样子
可以写成H(v)x = αe1
α = || x|| = （x₁² + x₂² + … x_n² ）^1/2
e = （1,0,0,0,0,…）^T

Oracle

Oracle直译为神谕，也是甲骨文公司的英文名字。
我画了个图表达Oracle的作用

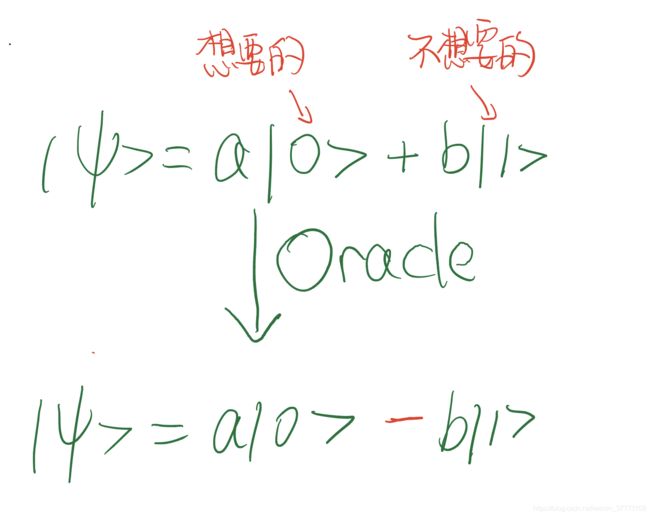
其实在我们这里可以简单地表示为它的作用是把叠加态中我们不想要的态给变成负的
肯定有人要疑惑又是生又是死的怎么就可以把死变负？？？
那咱也不懂啊，这就是数学表达quantum量子的trick了。
那这里就简单把Oracle理解为一个量子电路quantum circuit，这个电路是我们自己得设计的，他把我们不想要的一个态符号变负。

波函数

波函数wave function。虽然名字是叫函数，但其实使用向量的形式来表达的我把它理解成量子里面所有不好理解的东西、概念、定义就待搜索的数据全都一股脑的丢进去就完事了，包罗万象。
那在这里的话就是我们把数据写进波函数里面，然后量子搜索算法就在里面找。像如果是2¹⁵的空间中，波函数中为（0,0,0,0…,0,(0.7)^1/2,0…0,(0.29)^1/2,0…0,0,(0.01)^1/2,0,0…0,0）兄弟萌可以把0.7,0.29,0.01看做概率。像这样的一个空间的话，我们只需要量子电路迭代7次就能把（0.01）^1/2这个东西给找出来。
所以所这个玩意儿的复杂度是O((N/M)^1/2)的。N=全Hilbert空间大小，M=需要搜索的Hilbert空间的大小。

证明

可以参考grover搜索算法写的相当之nice

然后我这里尝试着证明但是卡住了，我对不起我的矩阵老师。

Grover算法总结

其实最关键最创新的点在于抓住了household矩阵的酉性质，将其与量子电路结合，再与叠加态这个概念结合，就能等到速度很快的搜索算法。这也对我后续的科研有积极地参考意义：利用矩阵的酉数学工具像奇异值分解呀，范数呀，将其与量子的一些基本假设相结合，或许会有意想不到的应用出现。
对比高考做数学题一样，做题可以顺序推导下去，但是科研比较自由就可以逆向，我们用一些数学理论工具，将一些酉矩阵与量子态乘乘加加，或许能有一些应用，发论文也更有数学背景。

量子推断

量子推断其实在本质上还是量子搜索算法（Grover算法）的应用。

流程

首先需要将所有的需要的数据写到波函数变量v中

x1 = [0 1 0; 0 1 0; 0 1 0; 0 1 0; 0 1 0]
x2 = [1 1 1; 0 0 1; 1 1 1; 1 0 0; 1 1 1]
x0 = [1 1 1; 1 0 1; 1 0 1; 1 0 1; 1 1 1]
nbit = 15
v = zeros(1< vec |> BitArray |> packbits)+1] = sqrt(p)

reflect的作用是构造一个reflect门电路，是用来构造household矩阵的。

rb = reflect(ArrayReg(ComplexF64.(v)))

psi0是搜索算法的要求，需要所有数据都是等概率振幅的。

A = repeat(nbit, H)
psi0 = apply!(zero_state(nbit), A) #ψ0 initial state
psi0 = ArrayReg(ComplexF64.(v))

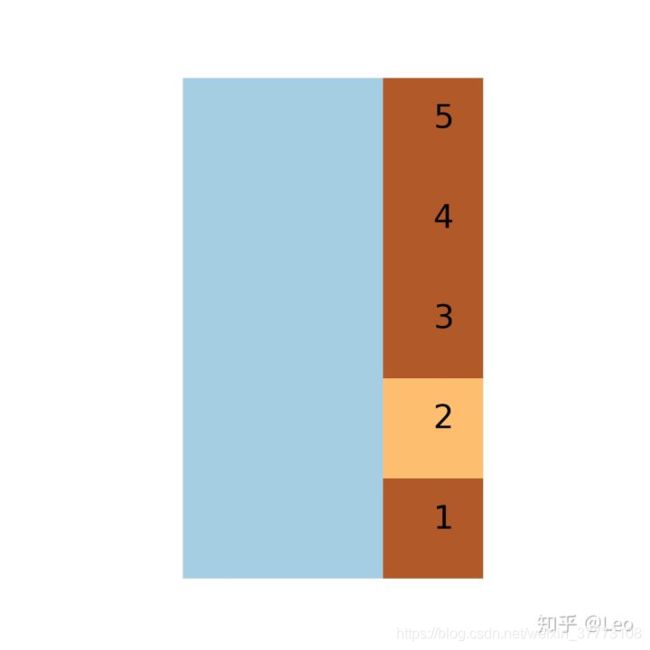
代码和图片都是来自Grover算法&量子推断by Leo
这里的12345是说将量子态apply到第12345个的电路上。
niter是迭代次数（7）
gb_infer是总的量子电路

# we want to find the digits with the first 5 qubits [1, 0, 1, 1, 1].
evidense = [1, -2, 3, 4, 5]
oracle_infer = inference_oracle(evidense)(nbit)

niter = num_grover_step(prob_match_oracle(psi0, oracle_infer))
gb_infer = chain(nbit, chain(oracle_infer, rb) for i = 1:niter)
# complete circuit

完整代码

By julia
And Yao

using Yao
using StatsBase, Test, LinearAlgebra
using BitBasis

nbit = 15
A = repeat(nbit, H)
ref = reflectblock(A)
psi0 = apply!(zero_state(nbit), A)
# data
x1 = [0 1 0; 0 1 0; 0 1 0; 0 1 0; 0 1 0]
x2 = [1 1 1; 0 0 1; 1 1 1; 1 0 0; 1 1 1]
x0 = [1 1 1; 1 0 1; 1 0 1; 1 0 1; 1 1 1]
    
nbit = 15
v = zeros(1< vec |> BitArray |> packbits)+1] = sqrt(p) 
            #matrx拉直成15*1       #packbits binary to int
end

########inference 线路构造

rb = reflect(ArrayReg(ComplexF64.(v)))
psi0 = ArrayReg(ComplexF64.(v))

# we want to find the digits with the first 5 qubits [1, 0, 1, 1, 1].
evidense = [1, -2, 3, 4, 5]
oracle_infer = inference_oracle(evidense)(nbit)

niter = num_grover_step(prob_match_oracle(psi0, oracle_infer))
gb_infer = chain(nbit, chain(oracle_infer, rb) for i = 1:niter)
# complete circuit
for (i, blk) in enumerate(gb_infer)
    apply!(psi0, blk)
    p_target = prob_match_oracle(psi0, oracle_infer)
    println("step $(i-1), overlap^2 = $p_target")
end
@testset "test reflect" begin
    reg = rand_state(15)
    ref_vec = apply!(zero_state(15), A) |> statevec
    v0 = reg |> statevec
 @test -2*(ref_vec'*v0)*ref_vec + v0 ≈ apply!(copy(reg), ref) |> statevec
end
##########################结果分析
nbit = 15
pl = psi0 |> probs #probs:Returns the probability distribution from a density matrix ρ. 
                    #psi0 is a density matrix?
config = findfirst(p->p>0.5, pl) - 1 |> bitarray(nbit)
res = reshape(config, 5,3)

参考文献

量子计算Grover搜索算法总结图文
grover搜索算法
添和 Leo 一起学量子算法: 二. Grover-Search 和量子推断

Yao
julia
维基