MATLAB机器人工具箱基础(一)
此文档作为自己学习过程中一个记录复习,基本来源于《Robotics, Vision & Control》这本书,可以作为matlab机器人工具箱的说明书来用,有兴趣可移步自行下载相关文档 机器人工具箱
坐标变换
- 位姿描述
- 二维
- 三维空间位姿描述
- 平移旋转组合
- 轨迹
- 平滑一维轨迹
- 多维
- 多段轨迹
位姿描述
二维
clc
clear all
%% 二维空间位姿描述
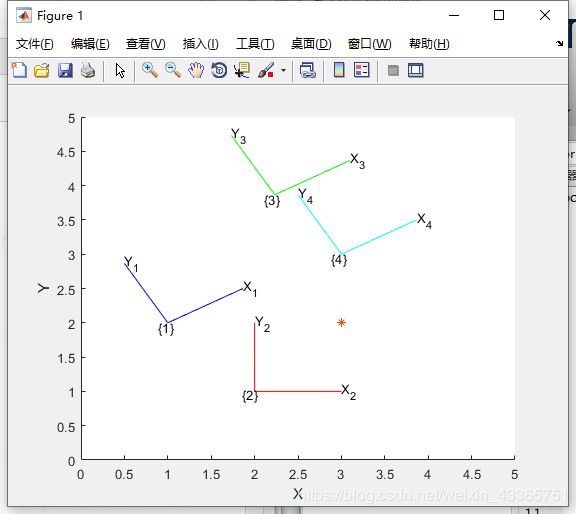
T1=se2(1,2,30*pi/180); %建立齐次坐标变换,代表(1,2)的平移和30°的旋转
trplot2(T1,'frame','1','color','b')%绘制变换坐标系,名字:{1} 颜色:蓝色
axis([0 5 0 5]);%坐标轴范围x为0-5 y为0-5
T2=se2(2,1,0) %齐次坐标变换:平移(2,1)零旋转的相对位姿
hold on
trplot2(T2,'frame','2','color','r');%绘制变换坐标系,名字:{2} 颜色:红色
T3=T1*T2
trplot2(T3,'frame','3','color','g');%绘制复合坐标系,名字:{3} 颜色:绿色
T4=T2*T1;
trplot2(T4,'frame','4','color','c');
p=[3;2];%相对世界坐标系定义点(3,2)
plot_point(p,'*')%把p点用*表示在图中
p1=inv(T1)*[p;1] %p点相对于坐标系{1}的坐标
h2e(inv(T1)*e2h(p)) %通过附加一个1 将欧几里得点转换为齐次形式。该齐次形式结果在坐标系{1}中有
% 一个负的y坐标,使用h2e函数可以进行反变换
%辅助函数e2h将欧几里得坐标点转换为齐次形式,而h2e进行逆转换
homtrans(inv(T1),p) %简洁的表达式
p2=homtrans(inv(T2),p) %p点相对于坐标系{2}的描述
三维空间位姿描述
三维空间是在二维情况的延伸,在二维坐标系上增加一个额外的坐标轴,通常用z表示与x轴y轴正交,z轴方向服从右手定则。
![]()
坐标系中的一个点p可以用其x,y,z坐标值或者一个约束向量表示
![]()
分别绕x,y,z轴旋转/theta角后的标准正交矩阵表示为:
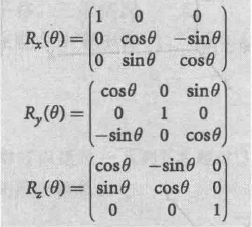
%% 三维空间位姿描述
R = rotx(pi/2)% 表示x轴的旋转矩阵
R = roty(pi/2)% 表示y轴的旋转矩阵
R = rotz(pi/2)% 表示z轴的旋转矩阵
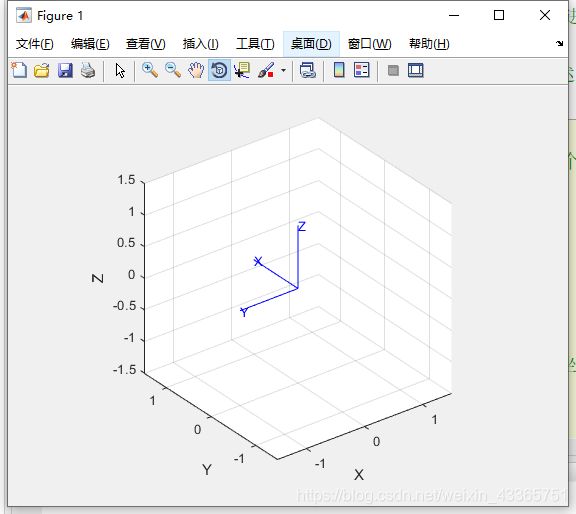
trplot(R,'frame','1','color','r') % 绘制坐标系
grid on
tranimate(R) %旋转动画,展示世界坐标系旋转到指定坐标系的过程
T=transl(1,0,0)*trotx(pi/2)*transl(0,1,0)
t2r(T) %提取矩阵中旋转矩阵部分
transl(T) %提取矩阵中平移部分
平移旋转组合
使用一个其次变换矩阵表示旋转和转换
transl 创建一个有平移但是无旋转的相对位姿
trotx 返回一个绕x轴旋转pi/2的4*4齐次变换矩阵,旋转部分与rotx(pi/2)相同,平移部分为零
用trplot(T)绘制相应坐标系
>>T=transl(1,0,0)*trotx(pi/2)*transl(0,1,0)
T =
1.0000 0 0 1.0000
0 0.0000 -1.0000 0.0000
0 1.0000 0.0000 1.0000
0 0 0 1.0000
>>t2r(T) %提取矩阵中旋转矩阵部分
ans =
1.0000 0 0
0 0.0000 -1.0000
0 1.0000 0.0000
>>transl(T) %提取矩阵中平移部分
ans =
1.0000
0.0000
1.0000
轨迹
一条路径只是一个空间结构——空间中从初始位姿过度到最终位姿的一个图形。轨迹是具有特定属性的一条路径
轨迹的一个重要特征是要平滑——位置和姿态随时间流畅的变化
平滑一维轨迹
从时间标量函数开始。这种函数的初始值和最终值是确定的,函数是光滑的(低阶时间导数是连续的,速度加速度是连续的,有时加速度的导数或加速度率也需要连续)
比较常用的五次多项式:![]()
其时间t《[0,T],其一阶和二阶导数也是光滑的多项式:

一般情况下速度加速度边界条件为零
在t=0和t=T时,分别将边界条件代入上述三个方程,得到六个方程,写成矩阵形式:

(一)
%% 五次多项式轨迹
限制条件为:起始终止速度、加速度为0,起点终点设定。六个条件
s=tpoly(0,1,50); %生成一个五次多项式轨迹,返回50*1列向量,其值在0-1范围内分50个时间步平滑变化
[s,sd,sdd]=tpoly(0,1,50); %相应的速度(sd)加速度(sdd)通过增加输出选项参数返回
subplot(3,1,1)
plot(s);xlabel('Time'); ylabel('s'); %绘制轨迹曲线
subplot(3,1,2)
plot(sd);xlabel('Time'); ylabel('sd'); %绘制速度曲线
subplot(3,1,3)
plot(sdd);xlabel('Time'); ylabel('sdd'); %绘制加速度曲线
%s=tpoly(0,1,50,0.5,0) %初始速度和终点速度默认值为0,也可设置非零值。初始速度0.5,最终速度0
mean(sd)/max(sd) %计算平均速度

(二)抛物线轨迹规划
每个机器人关节都有一个额定的最大速度,为了使关节运动时间最短,应该使运行在最大速度上的时间尽可能长,尽可能希望速度曲线顶部是一条平直线
一种公认的较理想的选择是采用混合曲线轨迹,中间的恒速段平直线加上两侧加速段和减速段多项式曲线构成的轨迹
lspb函数Linear Segment(匀速) with Parabolic(抛物线) Blends(过渡)
s=lspb(0,1,50)
[s,sd,sdd]=lspb(0,1,50); %参数与tpoly中的含义相同
subplot(3,1,1) %绘制轨迹曲线
plot(s);xlabel('Time'); ylabel('s');
subplot(3,1,2)
plot(sd);xlabel('Time'); ylabel('sd');
subplot(3,1,3)
plot(sdd);xlabel('Time'); ylabel('sdd');
max(sd) %函数lspb自动生成的直线段速度
s=lspb(0,1,50,0.025); %可以通过第四个输入参数为直线段指定一个速度
当设定匀速段速度时,随着速度的增加,匀速时间变短,加速度增大,振动会加大,所以匀速段速度要设置合理。
vmax = 2(lf - l0)/ tf,这里if/io分别为终止和初始位置,tf为时间
多维
将平滑的标量轨迹扩展为向量情况,可直接使用函数mtraj
eg:分50个时间步从(0,2)移动到(1,-1)可以表示为:
%x=mtraj(@tpoly,[0 2],[1 -1] ,50);
x=mtraj(@lspb,[0 2],[1 -1],50):
plot(x)
x=[transl(T);tr2rpy(T)]%三维空间中位姿,可以先将位姿齐次矩阵T转换为一个六维向量
得到一个50*2的矩阵x,每一行对应一个时间步,每一列对应一个轴,输入给mtraj,第一个参数是函数tpoly或lspyb,生成一个标量轨迹

多段轨迹
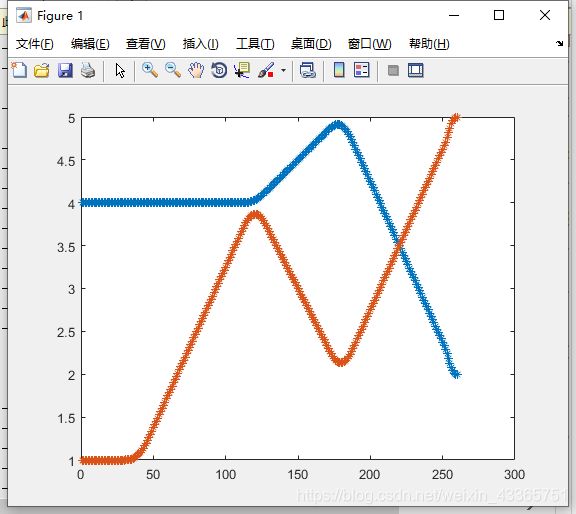
mstraj可以基于中间点矩阵生成一个多段多轴轨迹,例如,有4个中间点的两轴运动可以用:
via = [4,1;4,4;5,2;2,5];
q = mstraj(via,[2,1],[],[4,1],0.05,0);
plot(q,'*')
函数mstraj第一个参数是中间点矩阵,每点对应矩阵一行;每轴最大速度向量;没段运动时间向量;起点各轴坐标;采样时间间隔;加速度时间

函数mstraj返回一个矩阵,行对应时间每步,列对应各个轴
可以增加加速时间
q=mtraj(via,[2,1],[],[4,1],0.05,1);
plot(q,'*')