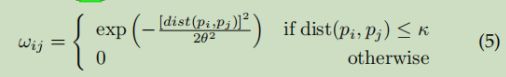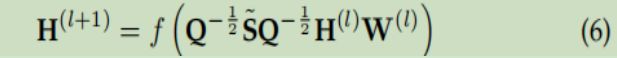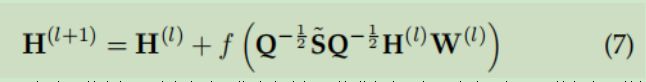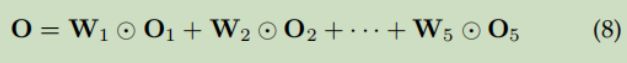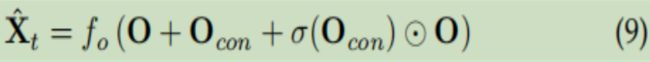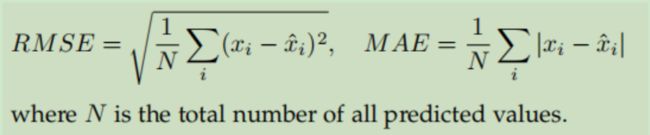MVGCN 人群流量预测模型 笔记

Predicting Citywide Crowd Flows in Irregular Regions Using Multi-View Graph convolutional Networks 笔记

作者：Junkai Sun, Junbo Zhang, Qiaofei Li, Xiuwen Yi, Yu Zheng

来源：arXiv:1903.07789v2 [cs.CV] 17 Jul 2020

1 论文背景与动机

       先前的工作主要集中在预测规则的网格化区域的人群流动。然而，城市实际上被道路网络隔开，非常不规则。预测城市不规则区域的人群流动，对于交通控制、风险评估和公共安全意义重大。

      人群流量预测问题是一个时空图(STG)预测问题，不规则区域为图节点，区域间过渡流用来构造边。但由于不同区域之间的相互作用和空间相关性，不规则区域人群流量预测比较困难，受到许多因素影响：

      1）STG不同顶点之间的相互作用和空间相关性。

      2）不同时间间隔之间的多重时间相关性：邻近性、周期性、趋势；

      3）复杂的外部因素（天气、事件）和元特征（一天的时间，周末/工作日）

       本文提出利用空间图卷积建立一个多视角图卷积网络(MVGCN)，用于人群流量预测问题，其中不同视角能捕捉到上述不同的因素。本文使用四个数据集来评估MVGCN，结果表明，MVGCN方法优于最先进的方法。

2论文创新

2.1提出一种GCN变体，它可以捕捉不同节点之间的空间相关性。设计多视图融合模块，将不同视图的多个潜在表示融合在一起。多视图融合有效地利用不同视图基于其特性的输出。

2.2 提出了一个综合框架，包括数据预处理、地图分割和地图聚类、过渡流构建图、GCN预测人群流量。

3论文模型

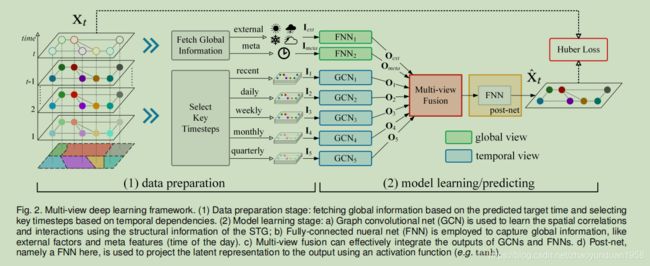
 该框架由数据准备和模型学习两个阶段组成：

1. 数据准备阶段：基于预测的目标时间获取全局信息（比如，如以前的时间步骤中的气象数据和天气预报。Iext and Imeta,），基于时间依赖（考虑两类时段（日，周)，两类趋势(月，季），选取相应的近期，日，周，月，季的时间步骤为重点 时间步骤，构建五个视图。）选择关键的 key timesteps（ 通过选择这些关键的时间步骤，MVGCN可以捕获多种类型的时间属性。）；然后将它们全部喂入到第二阶段进行模型训练。
2. 模型学习阶段：1）GCNs用STG结构信息学习（每个时间视图）空间相关性和相互作用，输出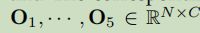；2)FNNs捕获全局信息，如外部因素和元特征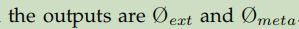， ；3）Multi-view fusion（多视角融合）集成GCNs和FNNs的输出；4）Post-net, 即FNN, 使用激活函数将潜在表示投影获得预测值，输出。

    人群流量预测问题——STG预测问题：

    节点——不规则区域；边——流出和区域之间的过渡流。

 

     Inflow-- 给定时间间隔内其他区域进入某区域的人群的总流量；

     Outflow--给定时间内离开某区域到其他区域的人群的总流量。

 

      通过在道路上行驶的汽车/自行车的数量、行人的数量、在公共交通系统上行驶的人数来衡量人群的流量。利用车辆的GPS轨迹来测量交通流量。

 map segmentation：

     1）利用形态学图像处理技术来处理区域划分任务，即将地图划分为2400个×2400个小网格单元，并将每个路点映射到其对应点网格单元，从而获得二值图像，1和0分别代表路段和空白区域。

     2）应用dilation和thinning得到路网骨架。

     3）使用连接分量标记算法(CCL)获得所有标记的不规则区域的位置，该算法通过聚类“1”标记的网格找到单个区域。

Map clustering:

       把两个低层区域之间的边缘权重定义为一个时段内的平均人群流量之间的Spearman's rankcorrelation coefficient。 小区域被聚集成一些高级别区域

Graph Construction——使用历史区域过渡流的拓扑图。

      从流量数据中选择一段时间，比如一到两个月。 然后，可以统计成对区域之间的有效时间切片。有效时间片是指考虑轨迹数据的噪声，当区域过渡流>α 当区域过渡的有效时间切片比大于阈值β时，PLA一个二进制值无向边来连接它们。α=3，β=0.1。

      每个顶点vi∈V都有一个地理空间位置pi和时变属性。这些属性在时间t上可以看作是图信号Xt∈RN×C，其中Xt[i，：]∈RC表示节点vi的C个属性，例如流入和流出（C=2）。 两个区域之间的边缘是由区域过渡流构造的。 两个区域之间的边缘是由区域向过渡流构造的，A中的二进制入口值表示两个区域在交通流中是否相关。

      模型输入：原始轨迹和道路网络。

      模型输出：城市的不规则区域的人群流入和流出（inflows/outflows）。

4 算法步骤

4.1 给定一个邻接矩阵A，根据空间距离为现有边分配空间权值。考虑了在STG中顶点的地理空间位置。 S∈RN×N是修正的邻接矩阵，；

4.2  ω∈RN×N是通过阈值高斯核加权函数计算的空间加权邻接矩阵。 dist(pi，pj)是指节点vi和vj之间的地理距离；θ和κ是控制邻接矩阵的尺度和稀疏性的两个参数。

4.3  stack M spatial graph convolutional layers  卷积整合了地理空间信息

4.4  为捕捉M-hop空间相关性和相互作用，叠加了M空间图卷积层。 当M很大时，我们需要一个非常深的网络。 残差学习允许神经网络具有100层的超深结构。通过叠加多个基于GCN的残差单元，可以构建非常深的神经网络来捕获多跳空间依赖

4.5 提出一种多视图融合方法，将许多流视图的潜在表示与两个全局视图（外部和元数据)融合。 不同的区域具有不同的时间性质。采用基于参数矩阵的融合方法将五个GCN的输出融合为时间视图。 W1—W5分别调节受临近、日周期、周周期、月趋势和季度趋势影响的程度。

 

4.6  Iext和元数据Imeta分别将喂入不同的FC层中，以获得不同的潜在表示Øext和Ømeta。 只需连接嵌入模块的所有输出，通过整形添加FC层，获得Ocon∈RN×C。

4.7不同的因素可能以不同的方式改变流动。利用两种不同的融合方法：对于逐步变化，采用求和融合方法， 对于突然的变化，用基于门控机制的融合，其中σ是一个近似的门控函数。当Ocon的级联表示捕获一些特殊的外部信息，如暴雨天气时， 由于sigmoid 函数性质，将突然增加，相比Ocon成为一个更大的值。而在大多数常见的情况下，它应该接近于零，没有突然的变化。基于两种融合方法，最终输出计算为

4.8 胡伯损失是和折衷， δ为阈值（默认值为1）.Huber损失结合了零附近平方误差损失和绝对误差损失理想性质。

5 论文实验

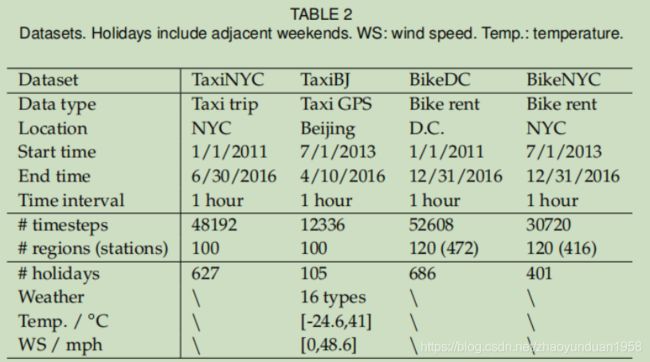
5.1 数据集

1）TaxiNYC：2011年1月1日—2016年6月30日纽约市的出租车GPS数据。 将NYC划分为100个不规则区域，据过渡流和区域间的地理距离建立图，计算人群流量。

2）TaxiBJ：北京出租车GPS数据，四个时间间隔：2013年7月1日—2013年10月30日，2014年3月1日—2014年6月30日，2015年3月1日—2015年6月30日，2015年11月1日—2016年4月10日。构图和人群流量计算方法与TaxiNYC相同。

3）BikeDC：取自华盛顿特区自行车系统。行程数据包括：行程持续时间，起止站ID，起止时间。共有472个站点。对于每个车站，两种流量，流入是进入自行车的数量，流出是签出自行车的数量。120个不规则区域。构造了这些区域之间具有过渡流和地理距离的图。

4）BikeNYC：取自纽约自行车系统，2013年7月1日—2016年12月31日轨迹数据。共有416个车站。 删除了不可用的自行车站点，并将其余的站点集中到120个区域。纽约市的图形构造和自行车流量计算方法与BikeDC相同。

 

上述四个数据集：测试集——最后四周的数据；训练集——所有剩余数据。

     本文过站点或区域之间的地理距离建立通勤网络(即图)，站点或区域可以看作是图中的节点。 每个站点都有地理空间位置。 对每个区域，近似地使用区域中心位置的地理空间位置。

5.2 对比方法

time-series models：    1）HA: Historical average     2）VAR: Vector auto-regressive

use the spatial and temporal features  3）GBRT: Gradient boosting decision tree

neural networks：

       4）FC-LSTM: Encoder-decoder framework using LSTM

       5）GCN:  3-layer supervised graph convolutional network

       6）DCRNN:  2-layer supervised diffusion convolutional recurrent neural network

       7）ST-MGCN: Forecasting ride-hailing demand with spatiotemporal multi-graph convolution network.

based on Gaussian Markov random fields：

       8） FCCF: Forecasting Citywide Crowd Flow model based on Gaussian Markov random fields

       9）FCCFno Trans

        说明：1）利用TensorFlow实现基于神经网络的模型，并通过反向传播和Adam[17]优化进行训练。  2）MVGCN模型以及大多数对比方法都用TensorFlow实现，模型训练过程在两个具有64GB RAM和16GB GPU内存的TeslaV100GPU上执行。训练时间因时间而异在不同的数据集上30分钟到3小时。

5.3  预处理

       使用Min-Max归一化方法将数据缩放到范围[1,1]或[0,1]。在评估中，将预测值重新缩放到正常值，并与真值比较。

对于外部因素，使用独热编码将元数据、假日和天气条件转换为二进制向量 使用Min-Max归一化将温度和风速缩放到[0,1]。

5.4 环境设置

      模型超参数设置如下：

1. 对于五个依赖序列的长度，lr、ld、lw、lm、lq∈{0，···，6}。
2. 图卷积层数设为{3，…，7}，不使用正则化。
3. 每个嵌入层的隐藏单元默认设置为10。
4. 训练数据分三部分：测试集——最后四周数据作为，验证集——相邻的前四周的数据作为，训练集——其余数据。验证集，通过早期停止控制训练过程以及基于最佳验证分数选择模型最终parameters。
5. 批次大小32。
6. 学习率定为0.0003。
7. 训练时间定为1000，提前停止耐心 设定为50。

       说明：对于所有训练的模型，只选择在验证集上得分最好的模型，并在测试集上进行评估。

5.5 评价指标

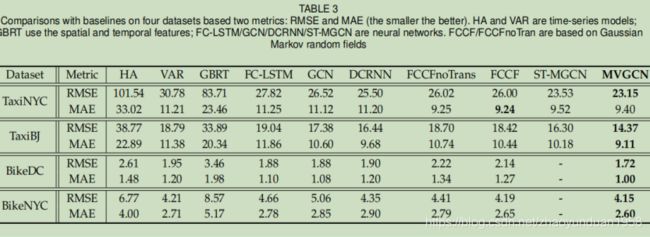
5.6 实验结果

实验证明： MVGCN在所有数据集上表现最好（除了MAE在出租车NYC）。

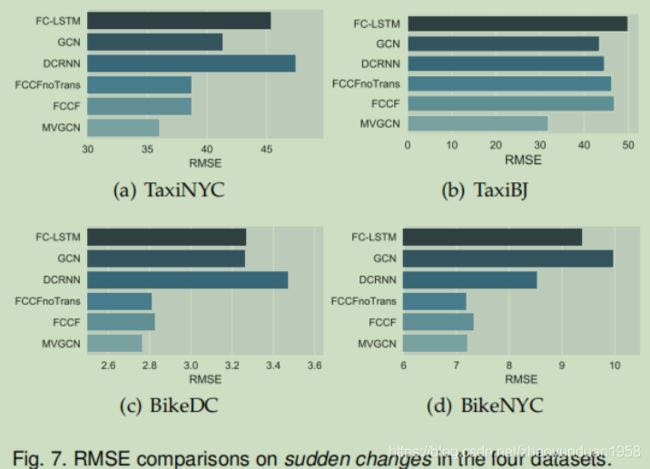
5.7  Results on sudden changes

   图7给出MVGCN与五条基线在突发变化情况下的比较，这可能是由异常天气或交通事件引起的。计算所有区域每个时隙t与t-1的交通流量差；将所有交通流差绝对值按降序排序，并将前5%时隙定义为发生突然变化的时间点，剩余95%时隙为正常情况。实验表明：MVGCN大大优于所有其他方法，特别是在出租车TaxiBJ。

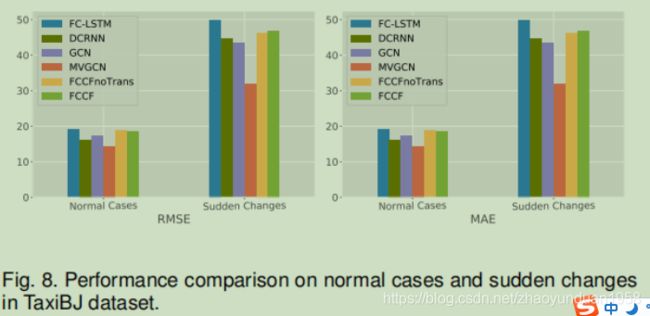
       如图8所示， MVGCN模型在正常情况和突然变化方面都比其方法表现得更好，此外，在后者取得明显改进。原因可能是MVGCN有效地建模天气数据。

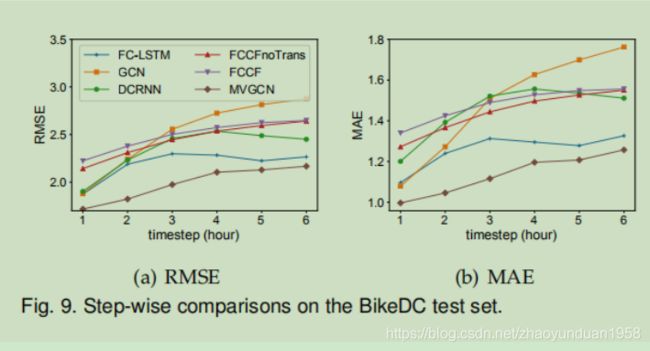
5.8 Results on multi-step prediction
      图9给出了基于RMSE和MAE的多步预测结果。对于单步预测模型，MVGCN，我们为不同的时间步骤训练不同的模型。
对于包括FC-LSTM和DCRNN在内的多步预测模型，使用前6个时间步长作为输入序列，接下来的6次作为目标序列，训练模特。 步数从1到6MVGCN 是鲁棒的，RMSE和MAE都有小的增加，在所有6时间步长中都达到了最佳效果。
随着时间步的增加，原始GCN是不稳健的。这表明如果我们以简单的方式将现有的模型应用于人群流量预测，它就不起作用。DCRNN表现不太好，因为它也只使用最近的时间步中的序列，导致它无法捕获周期、趋势和外部因素。

5.9  Effects of Different Components
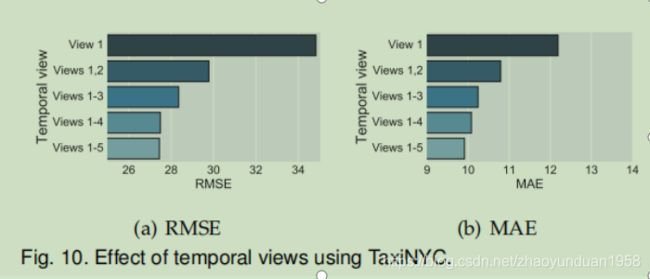
   图10展示了基于RMSE和MAE的不同时间视图组合的不同实验效果，包括最近（视图1)、每日(视图2)、每周(视图3)、每月(视图4）、季度视图（视图5）。 只要考虑最近的观点，就会得到一个糟糕的结果当考虑到日视图时，结果得到了很大改善，表明周期性是交通流模式的重要特征。此外，随着更多的时间视力图的考虑，结果变得越来越好。

5.10  Geospatial position
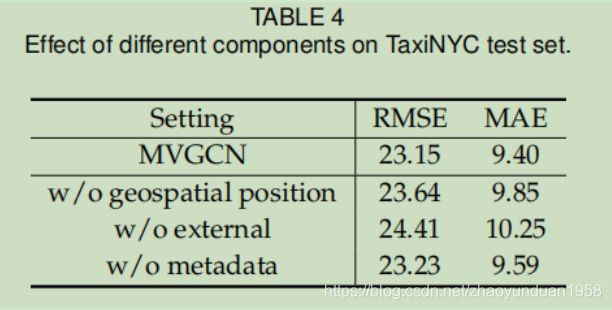
       没有地理空间信息，卷积层被降级为普通图卷积。表4显示：没有地理空间位置，RMSE从23.15增加到23.64，MAE也变得更差，证明了空间图卷积的有效性。

5.11 Global information

       论文比较了MVGCN在两种设置下的性能：去除外部因素或元数据，如表4所示。通过消除外部因素，RMSE从23.15增加到24.41。 同样，没有元数据，RMSE增加到23.23。 结果表明，外部因素/Meta数据影响STG的预测。

5.12 Huber loss and number of GCN layers

      为了进一步研究不同损失函数和GCN层数的影响。论文进行了一些消融研究，并报告了在TaxiNYC数据集上，不同空间图卷积层或损失函数的实验结果。

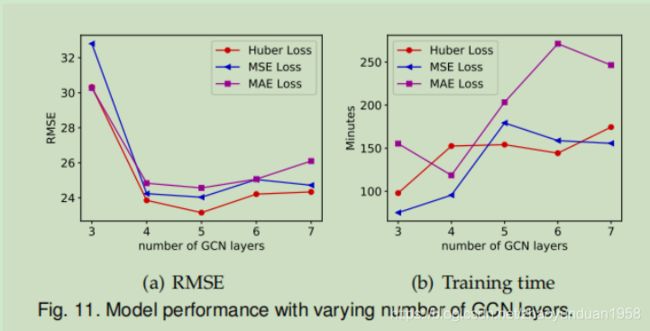
       图11显示，使用RMSE、MAE或Huber作为损失函数的性能首先下降，然后随着GCN层数量的增加而增加。当GCN层数为5时，会出现最佳结果。

       图11表明，深网络产生了更好的结果，但更深的网络仍然造成了共同的问题较高的预测误差。 早期停止的训练时间随模型深度的增加而增加。

 

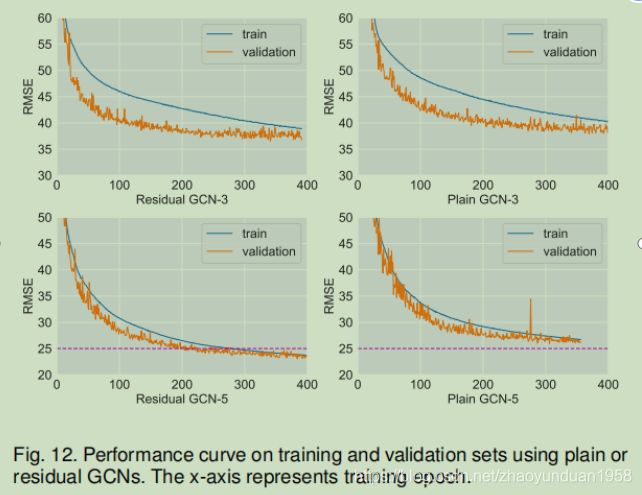
        为了验证残差GCN层的影响，论文将有残差的GCN单元与无残差的普通GCN层比较。，没有剩余连接。

        图12显示，两者在浅层网络中的表现相似。但当GCN的数量增加到5，残差网络可以获得更好的结果，并且它们都比浅层网络在适当的深度设置时表现得更好。

6. CROWD FLOW FORECASTING SYSTEM IN IRREGULAR REGIONS

      论文作者在内部开发了一个可以访问的不规则区域的人群流量预测演示（称为城市流量）

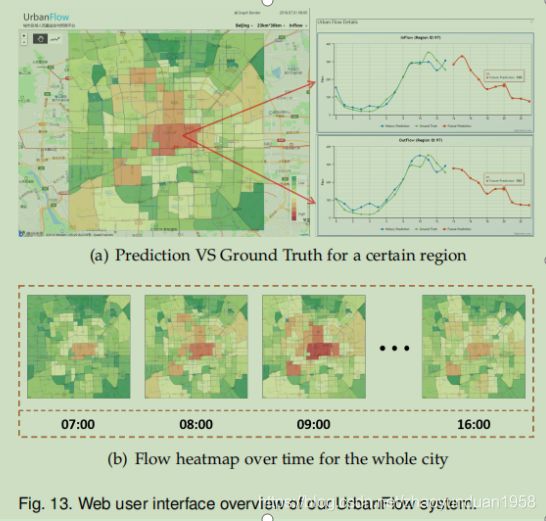
       图13(a)显示了系统中某个区域的流入和流出结果，其中绿线表示过去14小时的地面真实流入或流出，蓝色线表示14小时内的预测结果，橙色线表示未来10小时内的预测值。

       可以看到，绿色和蓝色线条有非常接近的值和相似趋势，这意味着MVGCN可以在交通流量预测系统中有效和良好地工作。

        图13(b)显示了整个城市不同时间戳的总体流量变化的另一个函数视图。 在早晨的高峰时间，大多数地区有更大的人群流动，因为人们从家里出发，而在下午，大多数人在工作或休息。