引言
哈希表(Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做哈希函数,存放记录的数组叫做散列表。散列表的设计核心是哈希函数的设计,设计的要求主要是下面两点:
1>哈希冲突的解决方法;
2>哈希冲突时的操作效率优化。
对于第一个问题,通常有两种方法:链表法和开放地址法。链表法就是将相同hash值的对象组织成一个链表放在hash值对应的槽位;开放地址法是通过一个探测算法,当某个槽位已经被占据的情况下继续查找下一个可以使用的槽位。
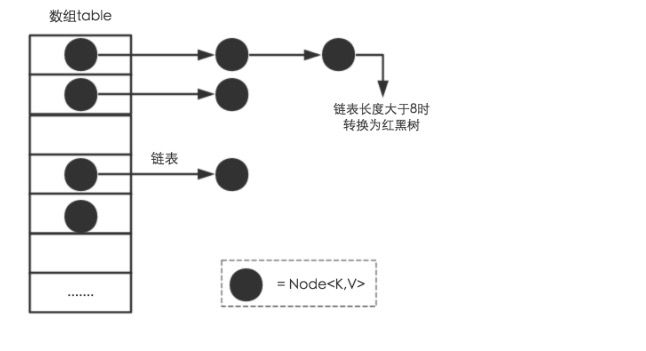
JDK的HashMap采用的链表法的方式,它的本质是一个链表数组,结合了数组查找快和链表删除和添加快的优点,提高访问效率,JDK1.8之前的HashMap采用数组+链表的方式实现,JDK1.8在此基础上,引入红黑树进行优化:当单链表的到达一定长度后,会升级成红黑树,这样对一个节点的访问效率从O(n)上升到O(lgn),n为链表的长度。
下面我们带着这些问题来分析一下HashMap的源码:
1>hash函数的设计;
2>从hashcode到索引的设计思想;
3>扩容的重新散列方法。
ok,下面我们开始分析它的源码实现吧!
HashMap源码分析
主要成员变量、常量和节点类型
//默认的数组容量,数组容量是2的指数幂(很重要)
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
//最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;
//扩容因子,当前size>=扩容因子*数组容量时,需要扩容
static final float DEFAULT_LOAD_FACTOR = 0.75f;
//单链表的长度大于等于8时单链表升级为红黑树
static final int TREEIFY_THRESHOLD = 8;
//红黑树节点小于等于6时候,退化成单链表
static final int UNTREEIFY_THRESHOLD = 6;
//当数组容量大于等于MIN_TREEIFY_CAPACITY才能存放红黑树节点,否则扩容,避免过多节点挂载到一个桶中
static final int MIN_TREEIFY_CAPACITY = 64;
//节点数组
transient Node[] table;
//有效的节点个数
transient int size;
//修改次数,hashmap非同步,避免同时修改
transient int modCount;
int threshold;//capacity * load factor
final float loadFactor;//外部设置扩容因子
节点类型有两种,Node用于单链表,TreeNode是Node的子类,当单链表需要升级为树时,Node转化为TreeNode.
Node封装了hashcode,键值对和后继节点指针。
static class Node implements Map.Entry {
final int hash;
final K key;
V value;
Node next;
Node(int hash, K key, V value, Node next) {
this.hash = hash;
this.key = key;
this.value = value;
this.next = next;
}
public final K getKey() {
return key;
}
public final V getValue() {
return value;
}
public final String toString() {
return key + "=" + value;
}
public final int hashCode() {
return Objects.hashCode(key) ^ Objects.hashCode(value);
}
public final V setValue(V newValue) {
V oldValue = value;
value = newValue;
return oldValue;
}
public final boolean equals(Object o) {
if (o == this)
return true;
if (o instanceof Map.Entry) {
Map.Entry e = (Map.Entry) o;
if (Objects.equals(key, e.getKey()) &&
Objects.equals(value, e.getValue()))
return true;
}
return false;
}
}
TreeNode主要成员变量如下:
static final class TreeNode extends LinkedHashMap.Entry {
TreeNode parent; // red-black tree links
TreeNode left;
TreeNode right;
TreeNode prev; // needed to unlink next upon deletion
boolean red;
TreeNode(int hash, K key, V val, Node next) {
super(hash, key, val, next);
}
...其他红黑树的操作方法
}
它继承LinkedHashMap.Entry,LinkedHashMap.Entry继承自Node,因此它是Node的子类,描述了红黑树的节点,封装了红黑树的查找、平衡插、平衡删除等操作,排序的依据是节点的哈希值。
HashMap的put方法
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
我们看到key又进行了一次hash:
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
它将key的哈希值的低16位于高16位做了抑或处理,因此处理后的哈希值的低16位隐含了高16位的信息,为什么这么做,我们看看注释:
/**
* Computes key.hashCode() and spreads (XORs) higher bits of hash
* to lower. Because the table uses power-of-two masking, sets of
* hashes that vary only in bits above the current mask will
* always collide. (Among known examples are sets of Float keys
* holding consecutive whole numbers in small tables.) So we
* apply a transform that spreads the impact of higher bits
* downward. There is a tradeoff between speed, utility, and
* quality of bit-spreading. Because many common sets of hashes
* are already reasonably distributed (so don't benefit from
* spreading), and because we use trees to handle large sets of
* collisions in bins, we just XOR some shifted bits in the
* cheapest possible way to reduce systematic lossage, as well as
* to incorporate impact of the highest bits that would otherwise
* never be used in index calculations because of table bounds.
*/
大致意思是,由于数组长度n为2次幂,做取模运算(后面会讲到)它产生的掩码(n-1)的低位全部是1,高位全部是0,那么,假如不对key的哈希值kh做处理,当kh的掩码上的所有低位相同,而高位不同时,都会产生碰撞,因此它将高16位与低16位进行抑或,处理后的低16位就隐藏了高地两段信息,高位发生变化时,低位也会发生变化,这样就避免大量哈希碰撞。
下面再看putVal方法:
/**
* Implements Map.put and related methods
*
* @param hash hash for key 加工后的哈希码
* @param key the key
* @param value the value to put
* @param onlyIfAbsent if true, don't change existing value
* @param evict if false, the table is in creation mode.
* @return previous value, or null if none
*/
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node[] tab;
Node p;
int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
//如果没有开辟数组,则扩容构建
n = (tab = resize()).length;
//index = (n - 1) & hash 相当于hash根据length取模(hash%len),只是位运算效率更高
if ((p = tab[i = (n - 1) & hash]) == null)
//如果数组中该位置为空,则放入新节点
tab[i] = newNode(hash, key, value, null);
else {//否则表示已经有元素占坑,
Node e;
K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
//当该节点的hash值相等且key相等,或者key与k相等时,说明找到key做替换
e = p;
else if (p instanceof TreeNode)
//key不相同,且节点为红黑树根节点,则往红黑树里添加元素
e = ((TreeNode) p).putTreeVal(this, tab, hash, key, value);
else {//Node为链表时,添加到链表中
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {//遍历到链表结尾,新节点挂载到链表结尾,退出遍历
p.next = newNode(hash, key, value, null);
//如果超过TREEIFY_THRESHOLD.链表转化成红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
//key命中时,也跳出遍历,此时节点e为命中节点
break;
p = e;//迭代下一个节点
}
}
//找到key命中的节点,替换value
if (e != null) { // existing mapping for key
//e != null 表示已经找到同样的key,更新value
V oldValue = e.value;
//onlyIfAbsent为只读标记,为ture时候,只有value为空,才做填充,否则不做覆盖操作
// onlyIfAbsent = false时直接更新
//onlyIfAbsent = true 且oldValue==null才更新
if (!onlyIfAbsent || oldValue == null)
e.value = value;//更新value
afterNodeAccess(e);
return oldValue;
}
}
++modCount;//fast-fail机制-修改计数
if (++size > threshold)
resize();//扩容
afterNodeInsertion(evict);
return null;
}
流程图如下:
说明:
1.从hash到桶索引的映射为取模操作,index= (n - 1) & hash,功能和hash%n一样,这里分析下为什么哈希表的容量一定要是2的整数次幂。首先,length为2的整数次幂的话,h&(length-1)就相当于对length取模,这样便保证了散列的均匀,同时也提升了效率;其次,length为2的整数次幂的话,为偶数,这样length-1为奇数,奇数的最后一位是1,这样便保证了h&(length-1)的最后一位可能为0,也可能为1(这取决于h的值),即与后的结果可能为偶数,也可能为奇数,这样便可以保证散列的均匀性,而如果length为奇数的话,很明显length-1为偶数,它的最后一位是0,这样h&(length-1)的最后一位肯定为0,即只能为偶数,这样任何hash值都只会被散列到数组的偶数下标位置上,这便浪费了近一半的空间,因此,length取2的整数次幂,是为了使不同hash值发生碰撞的概率较小,这样就能使元素在哈希表中均匀地散列。看到这里,结合前面对keyhash的处理,详细问题1和问题2的解也就水到渠成。
2.key的命中判断标准:
if (e.hash == hash &&((k = e.key) == key || (key != null && key.equals(k))))
hash相同不代表key命中,有可能是不同类对象的hash值相同,因此还需要判断key对象是否相同(==或者equals);
3.当索引位置的桶元素为空时,直接"占坑"即可,size加1;当桶元素不为空是,说明产生哈希碰撞,根据挂载类型(单链表或者树)查找key相同的节点,如果查到则覆盖value,否则新建节点挂载;后两种情况size不变;
4.执行put操作后,size有可能增加,超过阈值threshold,则进行扩容操作.
HashMap的get方法
相对于put方法,get方法的流程更加简单.看代码:
public V get(Object key) {
Node e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
final Node getNode(int hash, Object key) {
Node[] tab;
Node first, e;
int n;
K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
(first = tab[(n - 1) & hash]) != null) {
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
//桶元素key直接命中,直接返回
return first;
if ((e = first.next) != null) {//单链表或者树
if (first instanceof TreeNode)
//从红黑树中查找
return ((TreeNode) first).getTreeNode(hash, key);
do {
//从单链表中查找
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
流程这里不在赘述,put弄明白,get方法就更好理解了,这里不再赘述。下面看看HashMap如何扩容,这个方法才体现了设计者的精髓,我会详细说明。
HashMap的扩容方法
这里我们不着急看源码,先举个例子看看扩容后的索引变化:旧的数组容量为oldCap=16,扩容后新的容量为32,对于节点A(hash值为5)和B(hash值为21),有下面的分析:
节点A:oldIndexA = 0x1111 & 0x00101 = 0x101 = 5;
节点B:oldIndexB = 0x1111 & 0x10101 = 0x101 = 5;
n为2的幂次方,n-1则转化为hashcode的掩码,它只取hashcode的低位,实现了对数组长度的取余,保证索引不会越界。
当数组扩容到32时:
oldIndexA = 0x11111 & 0x00101 = 0x00101 = 5
oldIndexB = 0x11111 & 0x10101 = 0x10101 = 5 + 16 = 21
可见扩容后,hashcode掩码多了个1,掩码最高位对应的比特位为1时,就导致取模后的结果发生变化并且正好多了2的m次方,m为掩码的位数-1,恰恰就是旧数组的长度。那么问题来了,如何判断一个hashcode扩容之后,索引是否变化呢?前面说到看扩容后索引是否变化,主要看掩码的最高位对应的比特位上是否为1,而掩码的最高比特位正与旧数组长度的最高位(0x10...00)对应,所以只需要将hash值与oldCap做位与运算即可判断hash上的掩码的最高比特位是否为1,即:e.hash & oldCap,还是那个例子:
hashA & oldCap = 0x00101 & 0x10000 = 0;
hashB & oldCap = 0x10101 & 0x10000 = 0x10000;
经过这些分析,我们可以得出下面的结论
1.e.hash & oldCap为0时,oldCap扩容为oldCap<<1时,取模结果仍然不变;
2.e.hash & oldCap为1时,oldCap扩容为oldCap<<1时,取模结果变大,且增量为oldCap;
3.一次扩容,旧的哈希碰撞节点只可能分成两支,一支桶索引不变,另外一支索引为[旧索引+oldCap].
弄懂了这些分析,扩容代码就比较好理解了:
/**
* Initializes or doubles table size. If null, allocates in
* accord with initial capacity target held in field threshold.
* Otherwise, because we are using power-of-two expansion, the
* elements from each bin must either stay at same index, or move
* with a power of two offset in the new table.
*
* @return the table
*/
final Node[] resize() {
Node[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
} else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
} else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int) (DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float) newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float) MAXIMUM_CAPACITY ?
(int) ft : Integer.MAX_VALUE);
}
threshold = newThr;
//上面的代码都是参数的重新配置,只要知道newCap是oldCap的两倍即可,重点看下面
@SuppressWarnings({"rawtypes", "unchecked"})
Node[] newTab = (Node[]) new Node[newCap];//开辟新的数组,容量扩大两倍,仍未2的次幂
table = newTab;
if (oldTab != null) {
//旧数组迁移
for (int j = 0; j < oldCap; ++j) {//遍历旧的数组
Node e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)//老桶位置就只有一个元素
//重新散列获得新桶索引
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)//老桶位置为红黑树元素
//拆分
((TreeNode) e).split(this, newTab, j, oldCap);
else { // preserve order
//一个单链表或者树再扩容后,一部分元素挂载的通索引不变,
// 另外一部分会老桶位置的索引重新散列化后会后移
Node loHead = null, loTail = null;//较低位置的单链表,桶索引不变
Node hiHead = null, hiTail = null;//较高位置的单链表,桶索引后移
Node next;
do {
next = e.next;//遍历单链表
/**
* 举个例子
* oldCap=16(0x10000) --- hashA=5(101) hashB = 21(10101)
* --- oldIndexA = oldIndexB = (n - 1) & hash =
* oldIndexA = 0x1111 & 0x00101 = 0x101 = 5
* oldIndexB = 0x1111 & 0x10101 = 0x101 = 5
* n为2的幂次方,n-1则转化为hashcode的掩码,它制取hashcode的低位,
* 实现了对数组长度的取余,保证索引不会越界。
* 当数组扩容到32时:
* newCap = 32(0x100000), --- hashA=5(101) hashB = 21(10101)
* --- oldIndexA = oldIndexB = (n - 1) & hash =
* oldIndexA = 0x11111 & 0x00101 = 0x00101 = 5 (扩容后,散列后索引不变)
* oldIndexB = 0x11111 & 0x10101 = 0x10101 = 5 + 16 = 21(扩容后,散列后索引多了就数组长度)
* 此时二者低位相同,最高位为1,正好多了16即旧数组长度
* 扩容后掩码高了一位,对低位没有造成影响,下面再回头看看hash&oldCap:
* hashA & oldCap = 0x00101 & 0x10000 = 0;
* hashB & oldCap = 0x10101 & 0x10000 = 0x10000;
* 可以看到hashB虽然低位被,但在长度的最高位上为1,hashB相应的比特位上也为1,得出结果不为0,
* 由此可以得出它可以判断hashcode在旧的长度的最高Bit位上是否为1:
* 如果为1, 则扩容掩码比特位多了个1,散列索引必然发生变化,且索引增量为旧数组长度;
* 为0则散列化后的索引不变。
*/
if ((e.hash & oldCap) == 0) {
//e.hash & oldCap) == 0 表示hash散列化后不会越界,
//那么散列化后索引不变
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;//连接链表
} else {//散列化后索引变化,且增量为旧数组长度
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;//低索引设置头结点
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;//高索引设置头结点
}
}
}
}
}
return newTab;
}
分析到这前面提到的问题3也解决了.有关于remove方法和put方法思路基本一致,这里不在详细说明。
看完大神的轮子制造过程,明白原理,我们下一篇开始尝试造一个轻量级(基于数组和链表)的HashMap!