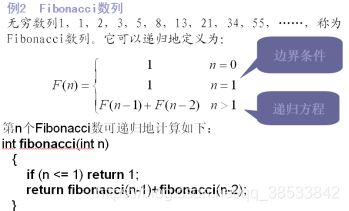
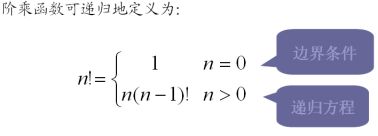计算机算法设计与分析--递归与分治策略(一)
一、分治法的设计思想:将一个难以解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
二、分治法的步骤
- 分解 :将原问题分解成一些规模较小的的相同问题,即子问题。
- 递归求解:对子问题递归求解。
- 合并:把子问题的解合并为原问题的解。
三、分治法能解决的问题一般具有以下几个特征
- 该问题的规模缩小到一定范围就可以很容易地解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
- 利用该问题分解出的子问题的解可以合并为该问题的解。
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
四、常见的例题
- 直接或间接地调用自身的算法称为递归算法。
- 用函数自身给出定义的函数称为递归函数。
- 递归函数的二个要素是边界条件与递归方程
例1-1
int Factorial(int n)
{
if(n==0) return 1;
return n*Factorial(n-1);
}
例1-2
(1)问题:设计一个递归算法生成n个元素{r1,r2,…,rn}的全排列。
(2)递归算法:
设R={r1,r2,…,rn}是要进行排列的n个元素,Ri=R-{ri}。
集合X中元素的全排列记为perm(X)。
(ri)perm(X)表示在全排列perm(X)的每一个排列前加上前缀得到的排列。R的全排列可归纳定义如下:
(一)当n=1时,perm®=®,其中r是集合R中唯一的元素;(边界条件)
(二)当n>1时,perm®由(r1)perm(R1),(r2)perm(R2),…,(rn)perm(Rn)构成。(递归)
(三)掌握perm函数
void perm(int a[],int k,int m) //k表示当前递归第一个数的位置,k从0开始,m为元素的个数
{
if(k==m)
{
for(int i=0;i<=m;i++) cout<<list[i];
cout<<endl;
}
else
{
for(int i=k;i<m;i++)
{
Swap(list[k],list[i]); //交换集合第i个和第k个元素,第k个元素排在前面
Perm(list,k+1,m); //递归求从第k+1至第m个元素的排列
Swap(list[k],list[i]); //交换回来
}
}
}
例1-4 Hanoi塔问题
(1)Hanoi塔问题
设a,b,c是3个塔座。开始时,在塔座a上有一叠共n个圆盘,这些圆盘自下而上,由大到小地叠在一起。各圆盘从小到大编号为1,2,…,n,
现要求以c塔为辅助,将塔座a上的这一叠圆盘移到塔座b上,并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则:
规则1:每次只能移动1个圆盘;
规则2:任何时刻都不允许将较大的圆盘压在较小的圆盘之上;
规则3:在满足移动规则1和2的前提下,可将圆盘移至a,b,c中任一塔座上。
要求:输入塔的层数,输出移动方式。
(2)递归算法:
第一步:以b塔为辅助把a塔上的n-1个圆盘移动到c塔上。(这是递归)
第二步:把a塔上的最后一个圆盘移动到b塔上。(这是边界条件)
第三步:以a塔为辅助把c塔上的n-1个圆盘移动到b塔上。(这是递归)
(3)掌握move函数和hanoi函数
#include五、典型问题
1.二分搜索
(1)问题:设a[0 : n-1]是一个已排好序的数组。实现二分搜索算法,使得当搜索元素x不在数组中时,输出提示。当元素x在数组中时,输出元素x在数组中的位置。
(2)二分搜索算法:
第一步:选取数组下标的中间值middle,如果a[middle]=x,那么查找成功。
第二步:如果x
第三步:直到查找到x,或者没找到,程序结束
(3)二分搜索算法满足分治法的四个适用条件:
- 该问题的规模缩小到一定的程度就可以容易地解决;
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质;
- 分解出的子问题的解可以合并为原问题的解;
- 分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
(4)掌握binarysearch函数
int binarysearch(int a[], int x, int n)
{
int left=0;
int right=n-1;
while(left<=right)
{
int middle=(left+right)/2;
if(a[middle]==x)
{
return middle;
}
else if(a[middle]<x)
{
left=middle+1;
}
else
{
right=middle-1;
}
}
return -1;
}
2、棋盘覆盖问题
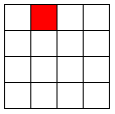
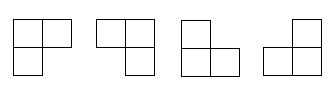
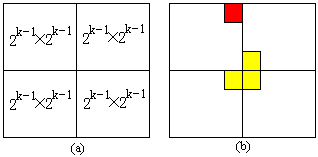
(1)问题:在一个2^k x 2^k 个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
(2)应用分治法:
第一步:当k>0时,将2^k × 2^k棋盘分割为4个2k-1×2k-1 子棋盘(a)所示。
第二步:特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,如 (b)所示。(边界条件)
第三步:这样将原问题转化为4个较小规模的棋盘覆盖问题。(递归)
第四步:递归地使用这种分割,直至棋盘简化为棋盘1×1。 (边界条件)
(3)掌握ChessBoard函数
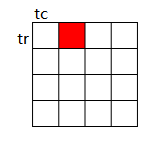
void ChessBoard(int tr,int tc,int dr,int dc,int size)
{
//用二维数组Board表示棋盘,Board[0][0]表示棋盘左上角的方格。
//tr和tc分别是棋盘左上角的行号和列号(1,1),dr和dc分别是特殊方格的行号和列号。
//size棋盘规格,Size=2^k中的k。
if(size==1) return;
int t=tile++; //tile表示L型骨牌编号。看运行结果可知,编号是什么无所谓。
int s=size/2;
//覆盖左上角子棋盘
if(dr<tr+s && dc<tc+s)
ChessBoard(tr,tc,dr,dc,s);//如果特殊方格在此子棋盘中,那么递归分割求解。
else
{
//如果此子棋盘没有特殊方格,那么:
Board[tr+s-1][tc+s-1]=t;//用t号L型骨牌覆盖此子棋盘的右下角。
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);//覆盖此子棋盘的其余方格。
}
//覆盖右上角子棋盘
if(dr<tr+s && dc>=tc+s)
ChessBoard(tr,tc+s,dr,dc,s);//如果特殊方格在此子棋盘中,那么递归分割求解。
else
{
//如果此子棋盘没有特殊方格,那么:
Board[tr+s-1][tc+s]=t;//用t号L型骨牌覆盖此子棋盘的左下角。
ChessBoard(tr,tc+s,tr+s-1,tc+s,s);//覆盖此子棋盘的其余方格。
}
//覆盖左下角子棋盘
if(dr>=tr+s && dc<tc+s)
ChessBoard(tr+s,tc,dr,dc,s);//如果特殊方格在此子棋盘中,那么递归分割求解。
else
{
//如果此子棋盘没有特殊方格,那么:
Board[tr+s][tc+s-1]=t;//用t号L型骨牌覆盖此子棋盘的右上角。
ChessBoard(tr+s,tc,tr+s,tc+s-1,s);//覆盖此子棋盘的其余方格。
}
//覆盖右下角子棋盘
if(dr>=tr+s && dc>=tc+s)
ChessBoard(tr+s,tc+s,dr,dc,s);//如果特殊方格在此子棋盘中,那么递归分割求解。
else
{
//如果此子棋盘没有特殊方格,那么:
Board[tr+s][tc+s]=t;//用t号L型骨牌覆盖此子棋盘的左上角。
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);//覆盖此子棋盘的其余方格。
}
}
3、合并排序
(1)合并排序问题:设a[0:n-1]是一个未排序的数组,如{12,45,3,6,29,4,16,77}。实现合并排序算法对该数组进行排序。
(2)基本思想:将待排序元素分成大小大致相同的2个子集合,分别对2个子集合进行排序,最终将排好序的子集合合并成为所要求的排好序的集合。
(3)合并排序步骤:
第一步:把数组划分成前后两半部分
第二步:递归排序前半部; 递归排序后半部分
第三步:合并
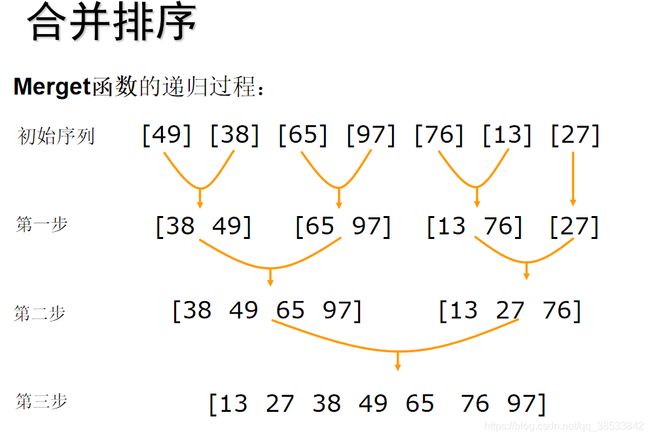
(4)掌握mergesort函数和merge函数
void mergesort(int a[],int left,int right)
{
if(left<right)
{
int i=(left+right)/2;;// 把数组划分成前后两半部分
mergesort(a,left,i);//递归排序前半部分
mergesort(a,i+1,right);//递归排序后半部分
merge(a,b,left,i,right);//合并到数组b,同时排序
copy(a,b,left,right); //复制回数组a
}
}
void merge(int c[],int d[],int l,int m,int r)
{
int i=l,j=m+1,k=l;
while((i<=m) && (j<=r))
{
if(c[i]<=c[j]) d[k++]=c[i++]; //先d[k]=c[i],然后k++、i++。
else d[k++]=c[j++];
}
if(i>m)
{
for(int q=j;q<=r;q++)d[k++]=c[q];
}
else
{
for(int q=i;q<=m;q++) d[k++]=c[q];
}
}
4、快速排序
(1)问题:设a[0:n-1]是一个未排序的数组,如{12,45,3,6,29,4,16,77}。实现快速排序算法对该数组进行排序。
(2)步骤
第一步:分解(Divide)
先从数据序列中选一个元素,称为基准元素。将序列中所有小于等于基准元素的元素都放到它的左边,大于等于基准元素的元素都放到它的右边。
在序列L[p…r]中选择基准元素L[q],经比较和移动后,L[q]将处于L[p…r]中间的适当位置,使得基准元素L[q]的值大于等于L[p…q-1]中任一元素的值,基准元素L[q]的值小于等于L[q+1…r]中任一元素的值。
第二步:递归求解(Conquer)
再对左右两边分别用同样的方法处理,直到每一个待处理的序列的长度为1。
通过递归调用快速排序算法,分别对L[p…q-1]和L[q+1…r]进行排序。
第三步:合并(Merge)
由于对分解出的两个子序列的排序是就地进行的,所以在L[p…q-1]和L[q+1…r]都排好序后不需要执行任何计算L[p…r]就已排好序,即自然合并。
这个解决流程是符合分治法的基本步骤的。因此,快速排序法是分治法的经典应用实例之一。
(3)选取基准元素的方法:
方法一:选取数组的第一个元素作为基准。(平常所说的快速排序)
方法二:从数组中随机选取一个元素为基准。(随机快速排序)
方法三:选取数组元素的中位数作为基准。(理想的快速排序)
(4)掌握partition函数和quicksort函数
int partition(int a[], int p, int r)
{
int i=p, j=r+1;
int x=a[p]; //第一个元素为基准
while(true)
{
while(a[++i]<x&&i<r);
while(a[--j]>x);
if(i>=j)break;
swap(a,i,j);
}
a[p]=a[j];
a[j]=x;
return j;
}
void quicksort(int a[],int p,int r)
{
if(p<r)
{
int q=partition(a,p,r);
quicksort(a,p,q-1);
quicksort(a,q+1,r);
}
}
(5)掌握randomizedpartition函数和randomizedquicksort函数
int randomizedpartition (int a[], int p, int r)
{
int i = Random(p,r);//随机选取基准
swap(a[i], a[p]);// 把准基放到第一位
return partition (a, p, r);
}
void randomizedquicksort(int a[],int p,int r)
{
if(p<r)
{
int q=RandomizedPartition(a,p,r);
Randomizedquicksort(a,p,q-1);
Randomizedquicksort(a,q+1,r);
}
}
5、线性时间选择
(1)问题1:给定线性序集中n个元素和一个整数k,1≤k≤n,要求找出这n个元素中第k小的元素。
问题2:给定n个元素和一个整数k,1≤k≤n,要求找出这n个元素中第k小的元素。
要求算法的时间复杂度是线性时间O(n)的。
(2)解问题2的方法一:模仿随机快速排序。
第一步:随机选取基准,划分数组,把不大于基准的元素都放到基准的左边,把大于基准的元素都放到基准的右边。
第二步:计算左边子数组的元素个数j,
如果j>=k,那么第k小的元素在左边子数组,这时在左边子数组递归查找。
如果j
int RandomizedSelect(int a[],int p,int r,int k)
{
if (p==r) return a[p];
int i=RandomizedPartition(a,p,r),
j=i-p+1;
if (k<=j) return RandomizedSelect(a,p,i,k);
else return RandomizedSelect(a,i+1,r,k-j);
}
(4)解决问题2的方法二 (四)掌握Select函数:
(一)思路: 选择近似中位数作为基准
(二)在数组中查找近似中位数的方法:
第一步:将n个输入元素划分成n/5个组,每组5个元素,只可能有一个组不是5个元素。用任意一种排序算法,将每组中的元素排好序,并取出每组的中位数,共n/5个。
第二步:递归调用select来找出这n/5个元素的中位数。如果n/5是偶数,就找它的2个中位数中较大的一个。以这个元素作为划分基准。
(三)方法二算法的步骤:
第一步:选取近似中位数作为基准,划分数组,把不大于基准的元素都放到基准的左边,把大于基准的元素都放到基准的右边。
第二步:计算左边子数组的元素个数j,
如果j>=k,那么第k小的元素在左边子数组,这时在左边子数组递归查找。
如果jint Select(int a[], int p, int r, int k)
{
int i;
if (r-p<75) {
quicksort(a,p,r);//用某个简单排序算法对数组a[p:r]排序;
return a[p+k-1];//返回数组第k小的元素
};
for (i = 0; i<=(r-p-4)/5; i++ )
{
quicksort(a,p+5*i,p+5*i+4);//对a[p+5*i]至a[p+5*i+4]的五个元素进行排序
swap(a,p+5*i+2,p+i);//将a[p+5*i]至a[p+5*i+4]五个元素中的第三小元素与a[p+i]交换位置,
//即将每组的第三小元素移到数组的前面去。
}
int x = Select(a, p, p+(r-p-4)/5, (r-p-4)/10);//递归调用Select函数对数组前几个元素寻找中位数。
//x是中位数的中位数(近似),(r-p-4)/5是原来数组元素五个一组的分组数(上面for循环里)。
i=partition(a,p,r, x);//与快速排序partition函数不同,多了一个参数x(基准)。
int j=i-p+1;//左半部分的元素个数
if (k<=j)
return Select(a,p,i,k);
else
return Select(a,i+1,r,k-j);
}