格子玻尔兹曼(LBM)小白的进阶之路

格子玻尔兹曼(LBM)小白的进阶之路

起因

2020年4月16日，距离新型冠状病毒爆发已经五个月的时间了，作为一名科研人员，高校迟迟未发开学通知，作为一名实验人员，第一次那么迫切希望可以熬夜做实验。但无论如何都回不到校园里，做实验，搞科研，写文章了。今天钉钉响了起来，导师发来一段简单的文字：最近的那篇文章好好写写，加点模拟的东西，发个高影响因子的期刊。再加上自己毕业需求，所以开始着手学习LBM模拟。B站一直是我的学习之源，这次很失望，没找到相关资源，网店上也没有找到相关书籍。于是抱着侥幸的心理百度了一下，然后就发现了CSDN这个社区。迫于现实开了一个月VIP， 下载了几篇相关的LBM书籍，目前主要还是先看何雅玲老师他们出版的《格子Boltzmann方法的理论及应用》。然后顺便在此做笔记，记录心得。书籍是在2008年出版的。鄙人能源相关专业，多相流为主要研究方向。
LBM，原来是Lattice Boltzmann Method的缩写，诞生到现在（2020）已经30多年了，算是新发展起来的模拟方法了。为进一步了解流动与传热机理，宏观尺度的实验研究和理论分析远远不够，需要从微观和跨尺度的介观角度进行深刻分析。因此而诞生LBM，该方法基于分子动理论，宏观上是离散方法，微观上是连续方法，因此又被称为介观模拟方法。具有天生的并行特性，边界条件处理简单，程序容易实施等优点，但理论体系尚不完善，国内应用还处于探索阶段（感觉现在很成熟了）。
何雅玲老师他们的书主要分为8个章节，所以我也基本上分成8部分进行笔记记录，心得随写。

第一章绪论

感觉自己基础知识不大牢固，不过感觉绪论应该不需要这些知识，所以就没有先去看附录里面的一些基本概念。先尝试往下走。
LBM是计算流体力学和计算传热学的一个新分支，流体力学最早可追溯到阿基米德时代，而传热学则产生于第一次工业革命时期。三大科学研究手段为实验研究，理论分析，数值模拟，相辅相成，缺一不可。计算流体和传热方法分为宏观方法、介观方法和微观方法。宏观层次上，流体被假设为连续介质，运动满足质量守恒、能量守恒和动量守恒，计算上通过离散将方程组离散成各种代数方程组，如有限差分法、有限容积法、有限元法、有限分析法、边界元法、谱方法，对应的商业软件有PHOENICS, FLUENT, STAR-CD, DFX。介观或微观层次，流体不再被假设为连续介质：微观层面上流体由大量的离散分子组成，如分子动力学模拟；介观层面上流体被离散成一系列的流体粒子（微团），常见的模拟方法有格子气自动机、LBM以及直接模拟蒙特卡罗方法。LBM 方法中除了流体被离散成流体粒子外，物理区域也被离散成一系列的格子，时间被离散成一系列的步长。描述流体粒子运动的方程被称为Boltzmann方程或相应的离散形式。第一篇关于LBM的文章最早出现在1988年。大致的改善过程如下：最早的格子气自动机—采用局部粒子分布函数和Boltzmann方程，形成多粒子碰撞模型（最初的LBM模型）—将碰撞算子线性化，形成矩阵模型—利用单松弛时间法简化平衡态，形成格子BGK(LBGK)模型—为消除降低压缩效应，提出多种等温不可压模型、不可压缩热模型（双分布函数模型），逐渐成熟。专业的商业软件为PowerFlow。多相流方面LBM模型主要有四种：着色模型、伪势模型、自由能模型以及其他模型（因为我主要的研究方向就是多相流）。采用LBM解决物理问题的基本步骤如下：

第二章 流体力学基本方程

大致看了一下第二章，感觉硬货来了，所以怂得我还是先看了附录A：笛卡尔张量的基本知识，把之前丢给流力老师的知识往回捡一捡。流力中物理量按其维数划分为标量、矢量和张量。三维空间中n阶张量可以由3^n个分量组成，所以标量其实是零阶张量，矢量是一阶张量，而二阶张量由9个分量表示。爱因斯坦求和约定：张量计算中同一项中如出现两个相同的下标，意味着对该指标求和，该指标称为哑指标。在方程同一项只出现一次的指标称为自由指标。没大看懂，特意百度了一下，看一下例子很好懂：

一个二阶张量可以看成是两个矢量的并矢。单位张量克罗内克定义及性质如下：

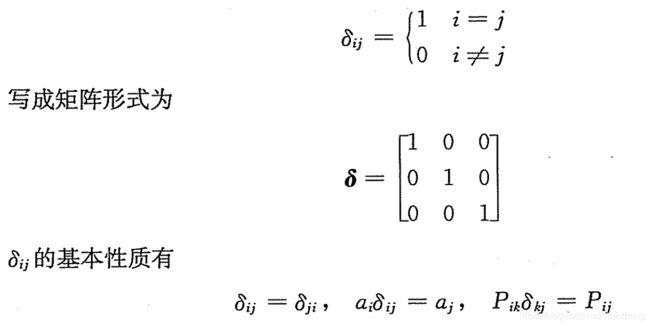
两个基矢量的点积便是单位张量。置换符号的定义和性质如下：

任何一个二阶张量都可以唯一地分解为一个二阶对称张量和一个二阶反对称张量的和。二阶张量的代数运算有相等、加减、点积和双点积。张量的微分、积分运算，主要包括梯度、散度、拉普拉斯算子以及高斯公式（这一块非常重要，需要着重理解）。

1. 梯度 （哈密顿算子）：
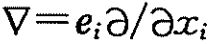
   其中标量进行梯度计算如下：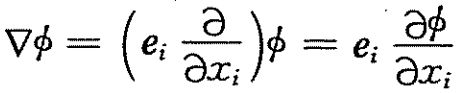
   矢量进行梯度计算如下: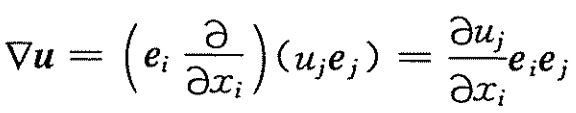
   一个n阶张量的梯度为（n+1）阶张量
2. 散度：相当于哈密顿算子与张量的点积。
   其中矢量的散度为：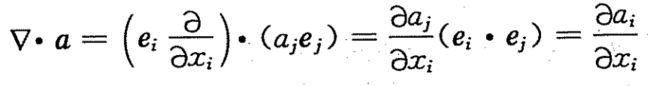
   二阶张量的散度为：
   
   一个n阶张量的散度为（n-1）阶张量
3. 拉普拉斯算子：先求梯度，再求散度：
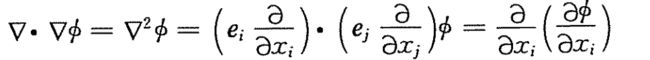
4. 高斯公式：
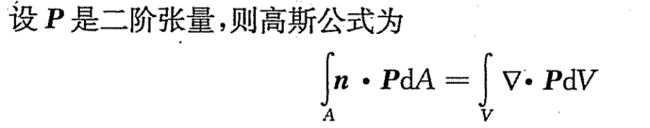
   自此基础知识就这些，感觉还可以，正式开始第二章的内容。第二章主要是推导了流体力学中的总能方程和内能方程，这两个方程对于LBM非常重要。首先讨论了流体力学中平均尺度的选取问题，进而提出连续介质的概念，引出连续介质假设（对于气体系统是否可以作为连续介质处理根据气体分子间的平均自由程λ与气体所处空间的代表性尺度L决定，即努森数Kn=λ/L。当Kn≤0.001时就可以作为连续介质处理；对于液体近代研究表明一直到微米尺度的液体层厚度，液体依然可以作为连续介质处理）。流体力学中研究的最小物质实体是流体质点，他在微观上充分大，宏观上又充分小。流体运动与能量传递的基本方程是根据质量守恒、动量守恒和能量守恒定律所建立起来的连续方程、动量方程和能量方程。

雷诺输运方程

流体力学中有两种方法描述流体运动：拉格朗日法（跟随流体质点研究流体运动的方法）和欧拉法（着眼于空间坐标研究流体运动的方法）。雷诺运输方程的作用是将一个流体系统的拉格朗日变化率表示为欧拉导数，从而将针对系统的物理量转换到易于研究的欧拉参考系中。通过各种推导和简化得到的雷诺输运方程如下：

连续方程（质量守恒）

根据质量守恒，通过带入雷诺输运方程得到连续方程如下：
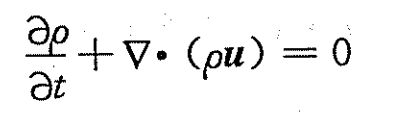或

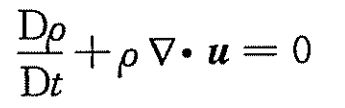
对于不可压缩流体（密度保持不变为常数）可进一步简化为：

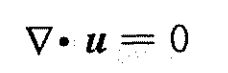
将连续方程和雷诺输运方程结合得到雷诺第二输运方程：

动量方程（动量守恒）

根据牛顿第二定律，系统内总动量的变化率等于作用在系统上的总质量力和作用在表面上的总表面力之和。得到的微分形式的动量方程为：

利用连续方程得到守恒形式的动量方程为:

该方程是从牛顿第二定律得到的，适用于任何一种流体。但对于牛顿流体，要得到更具体的动量方程，还需要引入牛顿流体的本构方程。在流力中本构方程一般专指应力张量与应变率张量之间的关系。根据斯托克斯假设可推导得出应力张量和应变率张量之间的关系为：

将该表达式带入微分形式的动量方程中得到Navier-Stokes方程（N-S方程）：

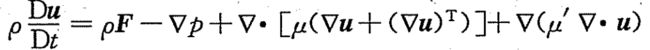
写成直角坐标系的约定求和形式为：

当温度很小时黏度可当成常数，方程可写为：

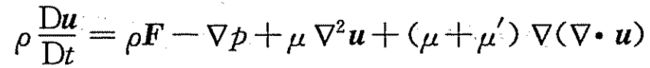
对于不可压流体进一步化简为：

上面两个式子利用连续方程得到守恒形式如下：

能量方程

结合热力学第一定律，总能方程为：

利用雷诺第二输运方程以及高斯公式将方程转化为：
所以微分形式的总能方程为：

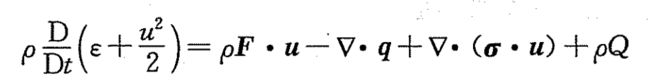
再展开得到：

动能方程两边点乘u,然后与总能方程相减可以得到内能方程如下：

表示单位体积流体内能的变化率等于流体变形时表面力的做功功率和向流体的传热功率之和。引入耗散函数后的内能方程为：

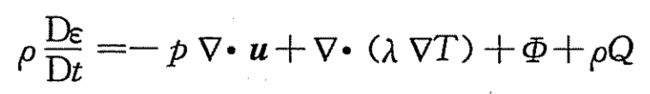
守恒形式为：

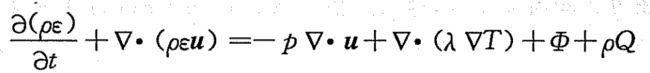
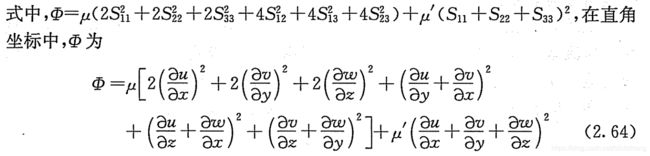
总结

本章推导了流体力学的三个基本方程：连续方程、动量方程和能量方程，守恒形式的方程组为：

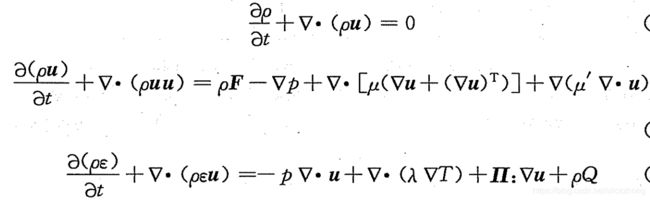
称为N-S方程组。其中压力和内能是密度和温度的函数，即：

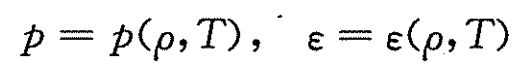
对于理想气体有：

上述方程动量方程是矢量方程，其余的都是标量方程，共计七个标量方程，未知量也是七个，包括密度、三个速度分量、压力、内能和温度。

第三章 LBM方法的基础理论和基本模型

格子方法的原则是：流体的宏观运动是流体分子微观热运动的统计平均结果，宏观行为对每个具体分子的运动细节并不敏感，N-S方程组所描述的守恒定律与微观粒子的运动规律是一致的，流体分子内部的相互作用差别反映在N-S方程组的输运系数上，因此可以构造微观模型或介观模型，使之在遵循基本守恒律的前提下尽可能简洁。
接下来按照Boltzman方程——Maxwell分布——Boltzman-BGK方程——格子Boltzman-BGK方程详细介绍格子Boltzman方程基础理论。

Boltzman方程

Boltzman方程基于气体动理论，这其中贡献最大的三位是克劳修斯、麦克斯韦和玻尔兹曼。Boltzman方程是统计力学中用以描述非平衡状态分布函数演化规律的方程。推导过程中有三个假设：
（1）分子互相碰撞时只考虑二体碰撞，即认为3个或3个以上分子同时碰撞在一起的可能性很小；
（2）分子混沌假设，这一假设认为各个分子的速度分布是不依赖另外的分子而独立的，即粒子在碰撞前速度不相关；
（3）外力不影响局部碰撞的动力学行为。
为简单起见，本书只讨论了单组分气体。引入速度分布函数f，通过推导、泰勒展开得到：

碰撞模型采用刚球模型，得到碰撞项表达式为：

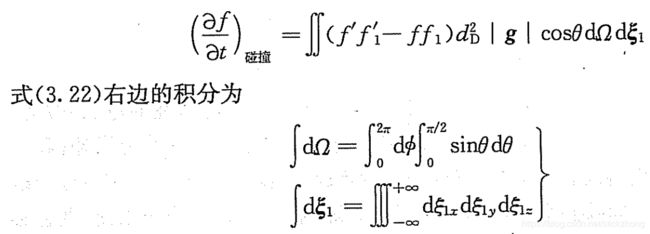
所以最后得到的Boltzman方程为：

该方程是气体动理论的基本方程，其右端项称为碰撞积分或碰撞项，通常用*J(ff1)*表示，该项的存在给Boltzman方程的求解带来极大的困难， 因此人们提出很多该项的近似解法进行简化。

Boltzman H定律及Maxwell分布

单组分单原子气体在不受外力时可得到Boltzman方程的一个解，即单组分单原子气体的平衡态分布——Maxwell分布。此分布基于Boltzman H定理。首先介绍了H定理。

通过一系列推导得到：

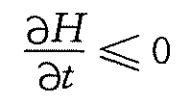
表明之前定义的H函数绝不会随时间变化而增加，这就是Boltzman H定理。这一定理说明当时间变化分布函数发生变化时，H总是减少的，当H减少到它的极小值而不再改变时，系统就达到平衡态，这体现了不可逆性。平衡态时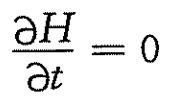，此时为Maxwell分布。这在且仅在如下等式成立时才有可能：

利用碰撞不变量和求和不变量得到Maxwell分布为：

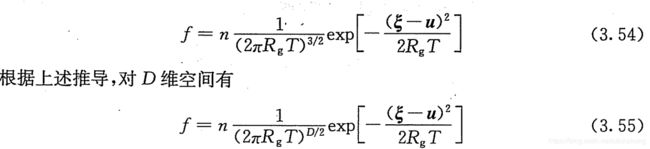
Maxwell输运方程及宏观量守恒方程组

Maxwell输运方程是将一个与分子相关联的量与Boltzman方程相乘并逐项对速度空间积分，即可得到Boltzman方程的矩，也称作矩方程。

分别求各项得到Maxwell输运方程如下：


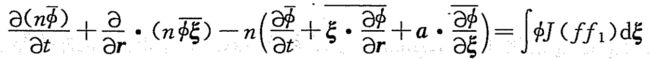
此时利用碰撞前后守恒可得到：

可得到连续方程
可得到动量方程
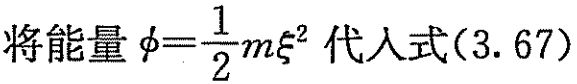可得到总能方程

从Boltzman方程到格子Boltzman方程

用简单的形式代替碰撞项，从而求解Boltzman方程得到流体的宏观流动。其中BGK近似就是在这一背景下产生的，但毕竟是用近似代替了准确项，存在缺陷。在BGK近似中
引入最简单的算子：

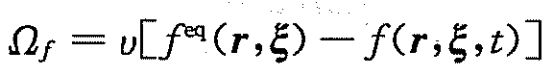
得到Boltzman-BGK方程如下：

引入弛豫时间可得到Boltzman-BGK方程为：

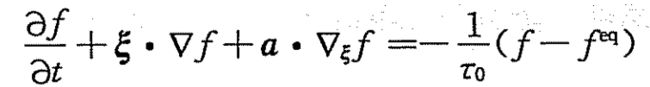
格子Boltzman是Boltzman-BGK方程的一种特殊离散形式。这一离散包括速度离散、时间离散和空间离散。速度离散后的Boltzman方程为：

要求解该方程还需要对其在空间和时间上进行离散，从而得到完全离散的Boltzman方程。沿特征线积分有：

这正是含外力项的格子Boltzman-BGK方程。

格子Boltzman方法的基本模型

一个完整的Boltzman模型通常由三部分组成：格子（离散速度模型，DVM），平衡态分布函数以及分布函数的演化方程。

DdQm（d维空间,m个离散速度）系列模型是Boltzman方法的基本模型。书中以D2Q9模型为例进行了说明。其离散速度如图所示：




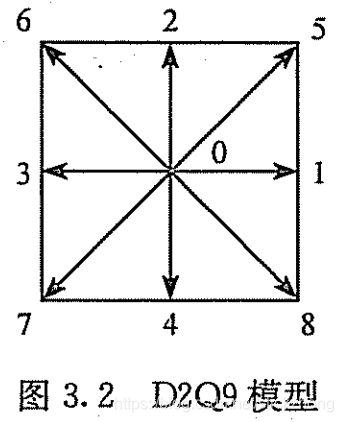
得到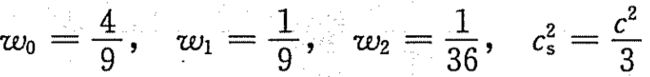
除了D2Q9外，其他常用的几个模型的离散速度、权系数以及声速如下：

接下来利用Chapman-Enskog展开（是一种多尺度技术）导出基本模型所对应的宏观方程。

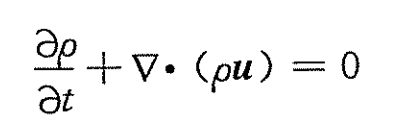
第四章 不可压格子Boltzman模型

上文利用Boltzman基本模型导出的宏观方程从形式上是可压缩的N-S方程组，用其模拟不可压流体时会存在一定的压缩误差，所以需对格子Boltzman基本模型进行改进使其恢复的宏观方程与标准的不可压N-S方程组相同或相近。（我们的研究基本上都是气体，具有一定的压缩性，所以这一部分可能不是那么重要）主要分为两个模型进行介绍，一个是不可压等温格子Boltzman模型，一个是不可压热格子Boltzman模型。

不可压等温格子Boltzman模型

是一个不断改进的过程：定常不可压模型（Zou-Hou模型）——一般不可压模型（He-Luo模型）——真正的一般不可压模型（D2G9模型）

不可压热格子Boltzman模型

用于不可压缩流体流动和传热的热格子Boltzman模型通常可以分为两类：双分布函数（DDF）模型和混合模型。在双分布函数模型中存在这两个分布函数：密度分布函数和内能（温度或总能）分布函数，其中密度分布函数用于模拟速度场，内能分布函数用于模拟温度场。双分布函数模型通常又可细分为：被动标量模型、内能分布函数模型和总能分布函数模型。双分布函数格子Boltzman模型分布函数的演化方程为：



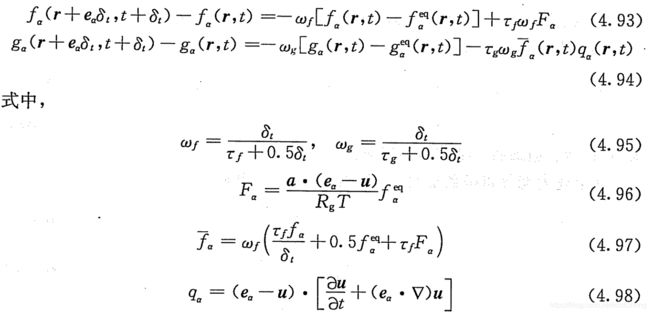
经过修改得到不可压的内能分布函数

但需要修改约束条件。

接着又介绍了基于Boussinesq假设的耦合双分布函数模型。这一假设由三部分组成：1）流动中的黏性热耗散忽略不计；2）除密度外其他物性为常数；3）对密度仅考虑动量方程中与体积力有关的项，其余各项中的密度亦作常数。

提出了一个基于Boussinesq假设的耦合的格子BGK模型，简称CLBGK模型。最后介绍了总能分布函数模型。

总能分布函数的演化方程得到如下：

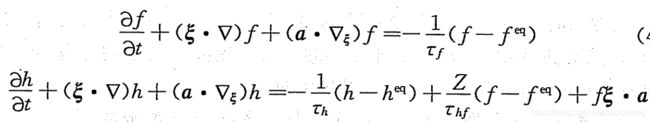
第五章 可压缩完全气体流动的LBM模型

由于流体运动而引起的可压缩性采用马赫数Ma来度量，Ma≤0.3，认为流体是不可压缩的；Ma＞0.3，流体表现出流动性。可压缩流动的格子Boltzman模型大体上可分为三类：多速度模型、比热容比可调模型以及耦合的双分布函数模型。下面对这三个模型分别进行介绍。

多速度模型

为求解其中的待定参数，分别定义了动量通量张量和热通量：

在多速度热模型中，除了保证质量、动量和能量守恒外，还应该满足平衡态动量通量张量为压力张量、平衡态热通量为0的条件，于是约束条件为：

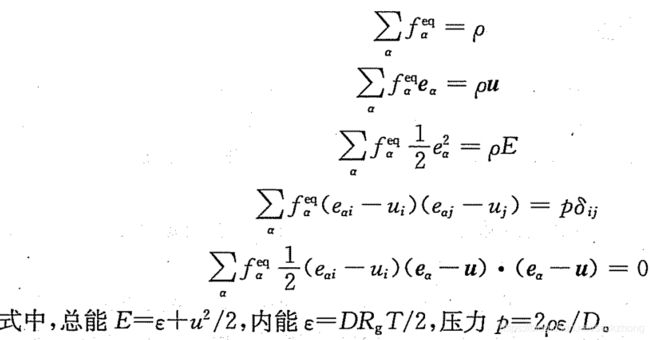
这两个多速度模型作Chapman-Enskog分析后存在不少问题，而后续的多个热模型或可压缩模型主要就是围绕解决这几个问题展开的。

Chen-Ohashi模型主要是针对多速度模型中存在非线性偏差项问题进行改进。


这种模型中普朗特数仍为常数，对于某个固定温度问题，比热容比依然不能自由选择。为解决普朗特数固定为常数问题，Chen等发展了一种双松弛因子方法

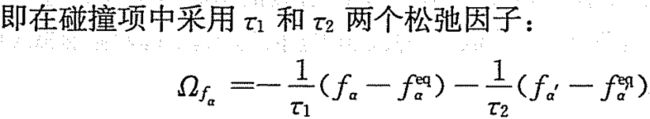
Chen-Ohashi模型满足了恢复正确宏观方程所应该满足的所有约束条件，但这一模型在进行具体数值模拟时并不一定可以提供令人满意的数值结果。为解决这一问题，Watari和Tsutahara提出另一种模型，确定平衡态分布函数的方法不同。

比热容比可调模型

多速度模型中能量只包括了粒子的平动动能，为拓宽LBM的应用范围，须寻求比热容比可调模型。1997年，Hu、Yan等将能级引入LBM方法中，首次实现LBM模型的比热容比可调。而在1998年，Sun在粒子能量的定义中引入了粒子势能。2001年，Shi等提出如下一种调节比热容比的总能定义方式：
2004年，Kataoka和Tsutahara提出了一个与Shi模型类似的总能定义方式：


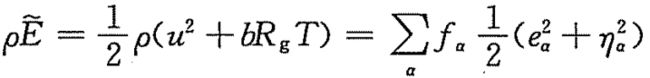
以上这些模型大部分应用范围主要还是局限于低中马赫数的可压缩流动。主要通过采用不同的平衡态分布函数来克服这一缺点，2007年，Qu和Shu提出一种新的构造平衡态分布函数的方法，用圆函数取代Maxwell分布函数，选择的圆函数如下：

从数值模拟结果来看，该方法建立的模型对高马赫数流动有着较好的适应性。

耦合的双分布函数模型

2007年Guo等提出的总能分布函数模型使得双分布函数格子Boltzman方法更为完善。按照两个分布函数是否耦合可将双分布函数模型分为两类：一类是非耦合的双分布函数模型，即流场影响温度场，而温度场并不反作用于流场；另一类是耦合的双分布函数。通过将双分布函数模型和多速度模型结合起来，提出了满足完全气体状态方程、可用于可压缩流动的耦合的双分布函数格子Boltzman模型。

格子Boltzman方法的边界处理

需要设法根据已知的宏观边界条件确定出边界节点上相应分布函数的取值，此过程中使用的方法被称为格子Boltzman方法的边界处理方法，所设计出的计算格式则称为边界处理格式。根据边界处理格式的特性分类如下：启发式格式、动力学格式、外推格式以及其他复杂边界处理格式。下文介绍均基于D2Q9模型以及格子Boltzman方程的碰撞迁移规则。

启发式格式

主要根据边界上诸如周期性、对称性、充分发展等宏观物理特性，通过微观粒子的运动规则直接确定边界节点上的未知分布函数，主要包括：周期性边界处理格式、对称边界处理格式、充分发展边界处理格式以及用于固体壁面处理的反弹格式、镜面反射格式、反弹与镜面反射混合格式。

周期性边界处理格式

该边界处理格式是指当流体粒子从一侧边界离开流场时，在下一个时步就会从流场的另一侧边界进入流场。

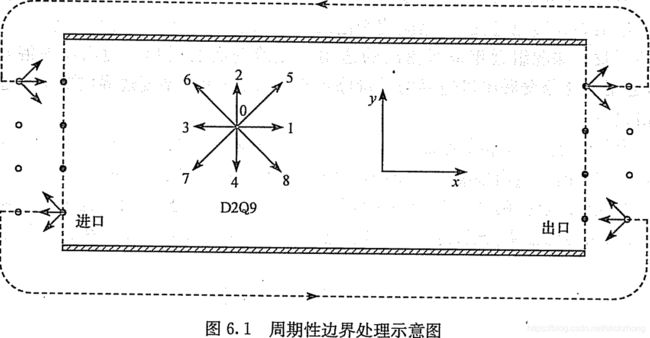
周期性边界处理格式表示为：

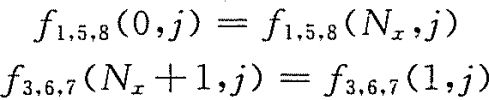
对称边界处理格式

为节省计算资源，取物理模型的一半作为模拟区域，并在对称轴上采用对称边界处理。

对称边界处理格式表示为：

充分发展边界处理格式

流体在通道内流动达到充分发展后，密度与速度等物理量在主流方向上不再发生变化，他们的空间导数为0.相应的边界处理规则如下：

这是处理充分发展边界最简单和常用的方法。同时速度更新法也常用于充分发展边界的处理。

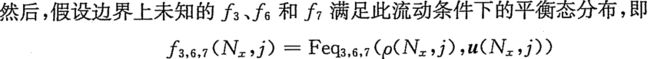
反弹格式

反弹格式包括标准反弹格式、半步长反弹格式及修正反弹格式。对于静止固体边界，常用的处理方法就是对边界上的粒子作弹回处理，称为标准反弹格式。

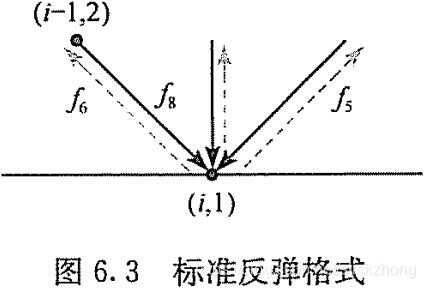
边界处理规则如下：

该格式操作简单，但只有一阶精度，为改进这一问题，采用修正反弹格式或半步长反弹格式，都具有二阶精度。修正反弹格式是考虑固体边界仍置于第一排节点上，在迁移过程之后下次碰撞过程之前，对于边界节点上的未知分布函数，令其与进入的流体粒子的分布函数相等，可以保证壁面上法向速度为0.剩下其他方向上的分布函数取进入边界的粒子分布函数的平均值，保证壁面上切向速度为0.碰撞过程中，边界节点与流体区域的节点一样，所有离散速度方向上的粒子均参与碰撞，得到的分布函数再进入下一碰撞迁移过程。半步长反弹格式如下：

镜面反射格式

上面的反弹格式主要用于无滑移壁面。对于光滑壁面，通常采用镜面反射格式实现自由滑移边界。具体实施如下：

反弹与镜面反射混合格式

微通道中的气体流动（主要研究方向）既不能用简单的反弹格式处理，也不能用镜面反射格式来描述气体与固体壁面之间的相互作用及动量交换。需要定义一个弹回比例系数rb（0≤rb≤1），来表示粒子在与壁面作用时沿原路弹回所占的比例。

动力学格式

动力学格式主要利用边界上宏观物理量的定义，直接求解边界节点上未知分布函数的方程组以获得边界节点上待定的分布函数。动力学格式主要包括：Nobel格式、非平衡反弹格式、反滑移格式和质量修正格式等。

Nobel格式

基本思想是：在边界节点速度已知的情况下，根据边界上的宏观量与分布函数之间的关系，确定边界节点的分布函数。不管是速度边界还是压力边界，实际上就是对流体施加一个外力作用，引起动量变化。所以需要在迁移和碰撞过程之间增加一个外力过程。该格式能求解的分布函数只有D+1个，超过这个限值则难以求解。

非平衡态反弹格式

反滑移格式

基本思想是：假设边界节点上的未知分布函数用一个新的平衡态分布函数代替，但为了克服壁面滑移，需要在这个平衡态分布函数中加入一个反滑移速度进行修正，该反滑移速度可以抵消采用反弹格式处理无滑移边界时产生的滑移速度，从而使得壁面上的流体速度与壁面速度相等。但反滑移格式通用性较差，应用范围有限。

质量修正格式

质量修正就是通过计算进口和出口的质量流率，确定一个质量修正系数，并以此系数修正出口速度，并用修正后的出口速度更新边界节点上的未知粒子分布函数。

外推格式

启发式格式和动力学格式局限性较大，很难推广到更一般的边界处理上。所以不少学者先后提出多种外推格式。

Chen格式

Chen等提出的外推格式具体做法是

由于可能计算出负的分布函数，因此数值稳定性较差。

非平衡态外推格式

Guo等人在2002年提出，其基本思想是，将边界节点上的分布函数分解为平衡态和非平衡态两部分，其中，平衡态部分由边界条件的定义近似获得，而非平衡态部分则采用非平衡外推确定。


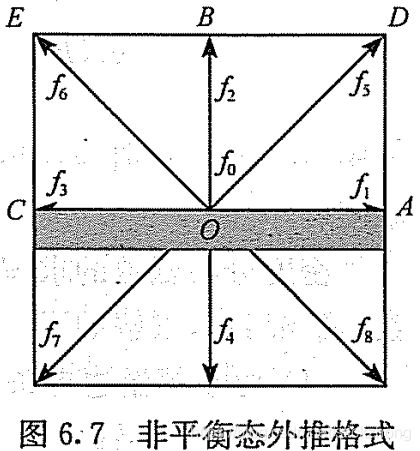
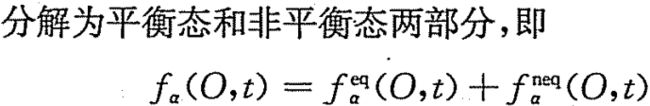
与其他边界处理格式相比，非平衡态外推格式具有很大的优势。

复杂边界处理格式

处理不规则边界时基于结构化的直角正交网格，在适当的位置采用阶梯逼近或插值处理，本节主要就是介绍基于直角正交网格下的插值处理。

Filippova与Hanel格式及其改进形式

他两提出构建虚拟平衡态分布函数，并用其进行线性插值的方法计算由壁面弹回流体的分布函数值。

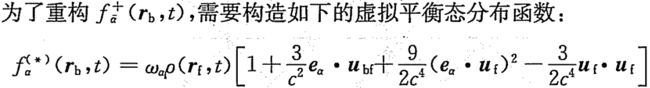
Bouzidi格式

提出了一种结合反弹格式和空间插值的边界处理方法处理任意曲率的复杂几何边界。该格式的基本思想是利用在弹回方向上用空间插值获得由边界进入流体的分布函数值。格式示意图如下：

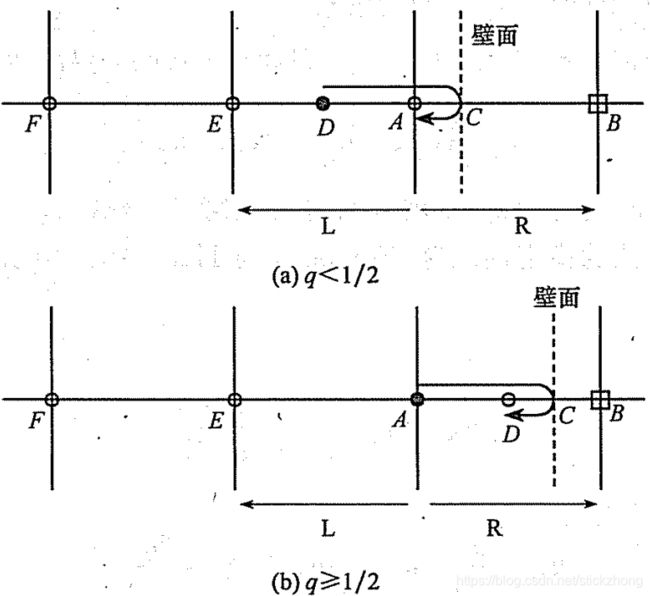
Lallemand与Luo格式

对Bouzidi格式进行了改进，即在引用插值公式时做了变化，把所有的分布函数统一到同一个时间层次上，同时考虑碰撞和迁移过程。

Guo格式

Guo等提出一种结合非平衡态外推格式和空间插值的曲线边界处理方法，其基本思想是将边界节点的分布函数分为平衡态和非平衡态两部分，平衡态部分由有个虚拟的平衡态分布函数代替，非平衡态部分则由相邻流体节点的非平衡态部分插值获得。

第七章 格子Boltzman方法的网格技术

标准格子Boltzman方法

代数方程（7.3）中若要求格子离散速度等于格子间距与时间步长的比值，则该方程为标准格子Boltzman方法的控制方程。
流体粒子的演化可分解为碰撞和迁移两个过程，碰撞过程为：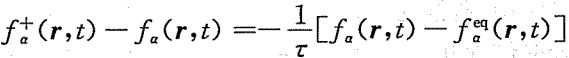
迁移过程为：
标准格子Boltzman方法也存在不足，不少学者提出多种改进技术。

插值格子Boltzman方法

在插值Boltzman方法中，碰撞迁移过程仍然保留，但由于网格不在均匀分布，迁移之后粒子所处位置不一定在固定网格节点上，因而需要增加一个插值过程确定网格节点的分布函数值。与标准Boltzman方法相比，非均匀网格计算需要在迁移过程之后，下一次碰撞过程之前增加一个插值过程。与标准Boltzman方法相比，额外的插值步骤增加了计算量，但由于网格数减少，综合而言，计算效率反而提高，为了减少数值误差，权衡计算量和计算精度的情况下，尽量采用高阶插值格式。

泰勒展开和最小二乘格子Boltzman方法

这种方法的基本思路是在标准格子Boltzman方法基础上引入空间上的泰勒级数展开和最小二乘法优化。这种方法对网格结构没有任何要求，具有无网格性，且可以用于任何速度模型，还可以达到二阶精度。

有限差分格子Boltzman方法

基本思想是采油有限差分方法对微分方程7.2求解，可以方便地使用非均匀网格，时间步长的选取也更加自由。不足之处在于放弃了标准格子Boltzman方法的碰撞迁移过程，程序操作较为复杂，且对于不同空间离散格式，会在不同程度上引入人工黏性，增加数值误差，对于复杂区域的适应性较差。

有限容积格子Boltzman方法

有限容积法是以积分型守恒方程为出发点，通过对计算域的离散来构造积分型离散方程，因而严格保证守恒特性，且便于应用不规则网格模拟具有复杂边界的物理问题。

有限元格子Boltzman方法

有限元方法是将计算域划分为一系列元体，在每个元体上取数个点作为节点，然后通过对控制方程积分来获得离散方程，并通过近似解来逼近微分方程的准确解。最大的优点是对不规则区域的适应性好，但计算量一般比较大。

多块网格

在物理量变化剧烈的区域采用比较密的网格，在变化缓慢的区域采用比较稀疏的网格，把流动区域划分为好几块结构化网格，每块结构化网格上仍采用标准Boltzman方法。

多重网格

多重网格方法是促进迭代求解收敛速度的有效方法。目前位置已有的多重网格格子Boltzman方法都仅能应用于稳态问题求解，对于非稳态问题还需要另外设计计算步骤。

第八章 格子Boltzman方法的应用举例

本章主要就格子Boltzman方法在模拟封闭方腔自然对流、Rayleigh-Benard自然对流、交变流动与换热、激波、声波衰减以及声学谐振腔六个例子展开叙述。