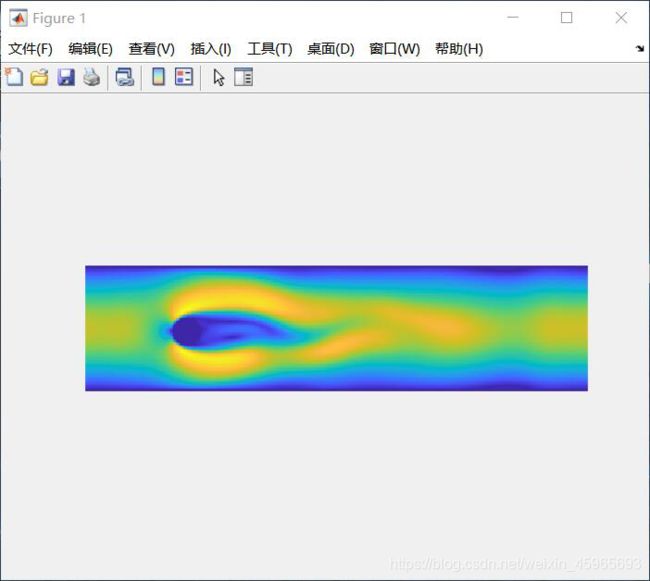
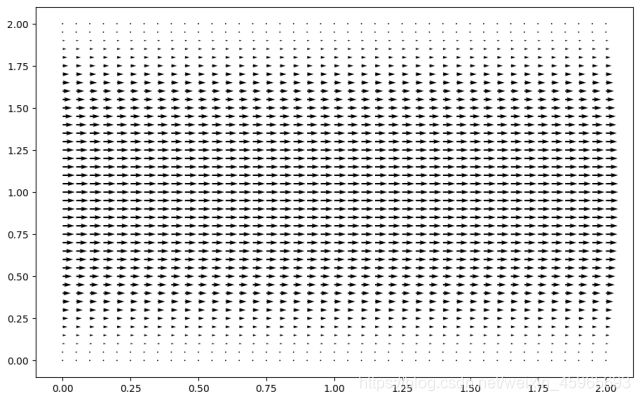
圆柱绕流
突然接触到了流体、CFD、LBM等等
入坑指南
传输过程数值模拟学习笔记
CFDPython 12 steps to Navier–Stokes
up效果非常棒
% =========================================================================
% Channel flow past a cylinderical obstacle, using a LB method
% =========================================================================
% Lattice Boltzmann sample in Matlab
% Original implementaion of Zou/He boundary condition
% =========================================================================
% =========================================================================
clear all
close all
clc
% =========================================================================
% GENERAL FLOW CONSTANTS --------------------------------------------------
lx = 400; % number of cells in x-direction
ly = 100; % number of cells in y-direction
obst_x = lx/5+1; % position of the cylinder; (exact y-symmetry is avoided)
obst_y = ly/2+3;
obst_r = ly/10+1; % radius of the cylinder
uMax = 0.1; % maximum velocity of Poiseuille inflow
Re = 100; % Reynolds number
nu = uMax * 2.*obst_r / Re; % kinematic viscosity
omega = 1. / (3*nu+1./2.); % relaxation parameter
maxT = 400000; % total number of iterations
tPlot = 50; % cycles
% =========================================================================
% D2Q9 LATTICE CONSTANTS --------------------------------------------------
t = [4/9, 1/9,1/9,1/9,1/9, 1/36,1/36,1/36,1/36];
cx = [ 0, 1, 0, -1, 0, 1, -1, -1, 1];
cy = [ 0, 0, 1, 0, -1, 1, 1, -1, -1];
opp = [ 1, 4, 5, 2, 3, 8, 9, 6, 7];
col = [2:(ly-1)];
in = 1; % position of inlet
out = lx; % position of outlet
[y,x] = meshgrid(1:ly,1:lx); % get coordinate of matrix indices
obst = (x-obst_x).^2 + (y-obst_y).^2 <= obst_r.^2; % Location of cylinder
obst(:,[1,ly]) = 1; % Location of top/bottom boundary
bbRegion = find(obst); % Boolean mask for bounce-back cells
% =========================================================================
% INITIAL CONDITION: Poiseuille profile at equilibrium --------------------
L = ly-2;
y_phys = y-1.5;
ux = 4 * uMax / (L*L) * (y_phys.*L-y_phys.*y_phys);
uy = zeros(lx,ly);
rho = 1;
for i=1:9
cu = 3*(cx(i)*ux+cy(i)*uy);
fIn(i,:,:) = rho .* t(i) .*( 1 + cu + 1/2*(cu.*cu) - 3/2*(ux.^2+uy.^2) );
end
% MAIN LOOP (TIME CYCLES)--------------------------------------------------
for cycle = 1:maxT
% MACROSCOPIC VARIABLES
rho = sum(fIn);
ux = reshape ( (cx * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho;
uy = reshape ( (cy * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho;
% MACROSCOPIC (DIRICHLET) BOUNDARY CONDITIONS -------------------------
% Inlet: Poiseuille profile -------------------------------------------
y_phys = col-1.5;
ux(:,in,col) = 4 * uMax / (L*L) * (y_phys.*L-y_phys.*y_phys);
uy(:,in,col) = 0;
rho(:,in,col) = 1 ./ (1-ux(:,in,col)) .* (sum(fIn([1,3,5],in,col)) + 2*sum(fIn([4,7,8],in,col)));
% Outlet: Constant pressure -------------------------------------------
rho(:,out,col) = 1;
ux(:,out,col) = -1 + 1 ./ (rho(:,out,col)) .* (sum(fIn([1,3,5],out,col)) + 2*sum(fIn([2,6,9],out,col)));
uy(:,out,col) = 0;
% MICROSCOPIC BOUNDARY CONDITIONS: INLET (Zou/He BC)
fIn(2,in,col) = fIn(4,in,col) + 2/3*rho(:,in,col).*ux(:,in,col);
fIn(6,in,col) = fIn(8,in,col) + 1/2*(fIn(5,in,col)-fIn(3,in,col)) ...
+ 1/2*rho(:,in,col).*uy(:,in,col) ...
+ 1/6*rho(:,in,col).*ux(:,in,col);
fIn(9,in,col) = fIn(7,in,col) + 1/2*(fIn(3,in,col)-fIn(5,in,col)) ...
- 1/2*rho(:,in,col).*uy(:,in,col) ...
+ 1/6*rho(:,in,col).*ux(:,in,col);
% MICROSCOPIC BOUNDARY CONDITIONS: OUTLET (Zou/He BC)
fIn(4,out,col) = fIn(2,out,col) - 2/3*rho(:,out,col).*ux(:,out,col);
fIn(8,out,col) = fIn(6,out,col) + 1/2*(fIn(3,out,col)-fIn(5,out,col)) ...
- 1/2*rho(:,out,col).*uy(:,out,col) ...
- 1/6*rho(:,out,col).*ux(:,out,col);
fIn(7,out,col) = fIn(9,out,col) + 1/2*(fIn(5,out,col)-fIn(3,out,col)) ...
+ 1/2*rho(:,out,col).*uy(:,out,col) ...
- 1/6*rho(:,out,col).*ux(:,out,col);
% COLLISION STEP ------------------------------------------------------
for i=1:9
cu = 3*(cx(i)*ux+cy(i)*uy);
fEq(i,:,:) = rho .* t(i) .* ( 1 + cu + 1/2*(cu.*cu) - 3/2*(ux.^2+uy.^2) );
fOut(i,:,:) = fIn(i,:,:) - omega .* (fIn(i,:,:)-fEq(i,:,:));
end
% =========================================================================
% OBSTACLE (BOUNCE-BACK)
for i=1:9
fOut(i,bbRegion) = fIn(opp(i),bbRegion);
end
% =========================================================================
% STREAMING STEP
for i=1:9
fIn(i,:,:) = circshift(fOut(i,:,:), [0,cx(i),cy(i)]);
end
% =========================================================================
% VISUALIZATION
if (mod(cycle,tPlot)==1)
u = reshape(sqrt(ux.^2+uy.^2),lx,ly);
u(bbRegion) = nan;
imagesc(u');
axis equal off; drawnow
end
end第二版本来自当码网(运行慢)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% cylinder.m: Channel flow pas a cylinderical %
% obstacle, using a LB method %
% %
% Copyright (c) 2006, Jonas Latt %
% %
% This program is released under the GNU %
% General Public License (GPL) %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear
ttt = cputime;
% GENERAL FLOW CONSTANTS
lx = 2500;
ly = 510;
obst_x = lx/5+1; % position of the cylinder; (exact
obst_y = ly/2+1; % y?symmetry is avoided)
obst_r = ly/10+1; % radius of the cylinder
uMax = 0.02; % maximum velocity of Poiseuille inflow
Re = 100; % Reynolds number
nu = uMax * 2.*obst_r / Re; % kinematic viscosity
omega = 1. / (3*nu+1./2.); % relaxation parameter
%maxT = 400000; % total number of iterations
maxT = 4000; % total number of iterations
tPlot = 2; % cycles
% D2Q9 LATTICE CONSTANTS
t = [4/9, 1/9,1/9,1/9,1/9, 1/36,1/36,1/36,1/36];
cx = [ 0, 1, 0, -1, 0, 1, -1, -1, 1];
cy = [ 0, 0, 1, 0, -1, 1, 1, -1, -1];
opp = [ 1, 4, 5, 2, 3, 8, 9, 6, 7];
col = [2:(ly-1)];
[y,x] = meshgrid(1:ly,1:lx);
obst = (x-obst_x).^2 + (y-obst_y).^2 <= obst_r.^2;
obst(:,[1,ly]) = 1;
bbRegion = find(obst);
% INITIAL CONDITION: (rho=0, u=0) ==> fIn(i) = t(i)
fIn = reshape( t'*ones(1,lx*ly), 9, lx, ly);
% MAIN LOOP (TIME CYCLES)
for cycle = 1:maxT
% MACROSCOPIC VARIABLES
rho = sum(fIn);
ux = reshape ( ...
(cx * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho;
uy = reshape ( ...
(cy * reshape(fIn,9,lx*ly)), 1,lx,ly) ./rho;
% MACROSCOPIC (DIRICHLET) BOUNDARY CONDITIONS
% Inlet: Poiseuille profile
L = ly-2; y = col-1.5;
ux(:,1,col) = 4 * uMax / (L*L) * (y.*L-y.*y);
uy(:,1,col) = 0;
rho(:,1,col) = 1 ./ (1-ux(:,1,col)).* ( ...
sum(fIn([1,3,5],1,col)) + ...
2*sum(fIn([4,7,8],1,col)) );
% Outlet: Zero gradient on rho/ux
rho(:,lx,col) = 4/3*rho(:,lx-1,col) - ...
1/3*rho(:,lx-2,col);
uy(:,lx,col) = 0;
ux(:,lx,col) = 4/3*ux(:,lx-1,col) - ...
1/3*ux(:,lx-2,col);
% COLLISION STEP
for i=1:9
cu = 3*(cx(i)*ux+cy(i)*uy);
fEq(i,:,:) = rho .* t(i) .* ...
( 1 + cu + 1/2*(cu.*cu) ...
- 3/2*(ux.^2+uy.^2) );
fOut(i,:,:) = fIn(i,:,:) - ...
omega .* (fIn(i,:,:)-fEq(i,:,:));
end
% MICROSCOPIC BOUNDARY CONDITIONS
for i=1:9
% Left boundary
fOut(i,1,col) = fEq(i,1,col) + ...
18*t(i)*cx(i)*cy(i)* ( fIn(8,1,col) - ...
fIn(7,1,col)-fEq(8,1,col)+fEq(7,1,col) );
% Right boundary
fOut(i,lx,col) = fEq(i,lx,col) + ...
18*t(i)*cx(i)*cy(i)* ( fIn(6,lx,col) - ...
fIn(9,lx,col)-fEq(6,lx,col)+fEq(9,lx,col) );
% Bounce back region
fOut(i,bbRegion) = fIn(opp(i),bbRegion);
end
% STREAMING STEP
for i=1:9
fIn(i,:,:) = ...
circshift(fOut(i,:,:), [0,cx(i),cy(i)]);
end
% VISUALIZATION
if (mod(cycle,tPlot)==0)
u = reshape(sqrt(ux.^2+uy.^2),lx,ly);
u(bbRegion) = nan;
imagesc(u');
axis equal off; drawnow
end
end
ett = cputime-tttpython版来自GitHub(需要自学自写)
不搬运了