对流图的遍历

  正常的图遍历有DFS和BFS，CFG作为图的一种自然也是如此，不过在CFG中，BFS的应用貌似并不多。

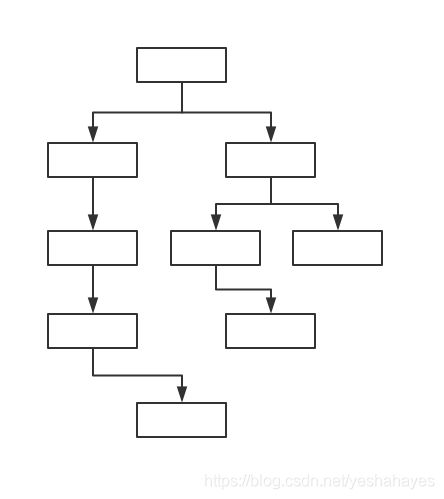
1，深度优先生成树，树边，前向边，后向边，横边。

  在DFS的过程中，按照如下规则标记图中的所有边：

1. 存在一条边从一个节点指向其后代，并且之前没有被标记过，则将该边标记为树边（tree edge）。
2. 存在一条边从一个节点指向其祖先或自身，将改边标记为后向边（back edge）。
3. 存在一条边指向其后代，但已经被标记，将其标记为前向边（forward edge）。
4. 不满足上述条件的边（即既不指向祖先，又不指向后代）标记为横边（cross edge）。

  由所有树边组成的一棵树称为图的深度优先生成树(depth-first spanning tree,DFST)。深度优先生成树必须包含途中的所有节点。

深度优先生成树

  同一个CFG可能会产生不同的DFST。

2，前序，后序，逆后序。

  在DAG中，优先访问当前节点构成的序列就是DAG的前序序列（pre order），在访问子节点后再访问当前节点构成的序列就是DAG的后序序列（post order），而将后序的顺序倒过来，则构成逆后序序列（reverse-post order，RPO）。

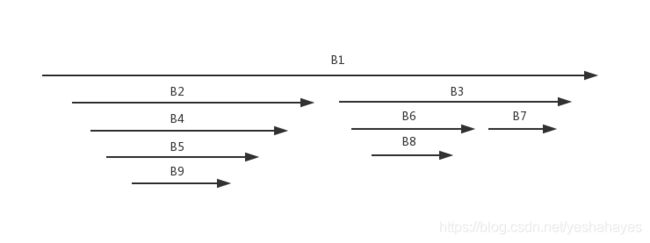
  在上图中，前序序列为：B1,B2,B4,B5,B9,B3,B6,B8,B7。后序序列为：B9,B5,B4,B2,B8,B6,B7,B3,B1。逆后序为：B1,B3,B7,B6,B8,B2,B4,B5,B9。

  可以看出，后序蕴含着控制流执行顺序的逻辑关系，在后序遍历中，当前节点的位置必然会在其所有子节点之后，相应的，在逆后序中，当前节点的位置也必然在其所有子节点之前，其实这就构成了DAG的拓扑排序序列。但前序序列不然，比如上例中，B9显然不会在B3之前执行。

  后面会看到，在迭代向前传播数据流的过程中，如果数据流值时沿着逆后序的序列传播的话，迭代收敛的速度会快于其他的序列，反之亦然。

  CFG和DAG相比多了后向边，即从局部来看，逆后序在前的节点不一定比后面的节点更早的执行。但是对于可规约流图，后向边并不会改变其拓扑顺序，所以在可规约流图上，可以简单的去除后向边后转换为DAG，并得到一个近似的拓扑排序序列RPO。（不可规约流图是否也有类似的性质呢？）

  事实上，我们可以发现，对于一个CFG，如果有一条边m->n，rpo(m)>=rpo(n)，那么这条边就是一个后向边，所有的循环结构必然包含这样一条边，可以用这个性质来识别循环体。

3，DFS序与括号定理。

  在DFS过程中，分别给每个节点添加前序遍历和后序遍历的时间戳，每个节点的起始和结束时间戳被称为DFS序。

  基于DFS序有括号定理，即任意两个节点只有如下三种情况：

• 两个节点的DFS序不互相包含。
• 节点m的DFS序包含节点n的DFS序，则m是DFS中n的祖先。
• 节点m的DFS序包含于节点n的DFS序，则m是DFS中n的后裔。

  利用括号定理，可以快速的确定分支或者循环的子结构。

上图的DFS序。

4，BFS。
  好像用到BFS的地方并不多，本人见识短浅，目前只在一篇论文中见过，等到要用的时候再说。

5，代码实现。

  常规操作，不过考虑到可能会操作不同的Block（语法的，ir的和机器码级别的），这里将Block进行模板化：

	template<typename BBTy>
	class DfsTraversal {
	public:

		using BBOrderList = vector<BBTy*>;

		struct TimeStamp {
			unsigned enter;
			unsigned exit;
		};

	private:

		BBOrderList PreOrder;
		BBOrderList PostOrder;
		BBOrderList ReversePostOrder;

		map<BBTy*, TimeStamp> DfsTS;

		unsigned TimeTick;

		void dfsVisit(BBTy* root, set<BBTy*>& visited) {

			visited.insert(root);
			PreOrder.push_back(root);
			DfsTS[root].enter = TimeTick++;

			for (auto i : llvm::make_range(succ_begin(root), succ_end(root))) {
				if (visited.count(i)) {
					continue;
				}
				dfsVisit(i, visited);
			}

			PostOrder.push_back(root);
			DfsTS[root].exit = TimeTick++;
		}

	public:

		void calculate(BBTy* entry) {

			set<BBTy*> visited;
			TimeTick = 0;

			dfsVisit(entry, visited);

			for (auto i = PostOrder.rbegin();i != PostOrder.rend();++i) {
				ReversePostOrder.push_back(*i);
			}
		}

		BBOrderList& getDFSPreOrder() {
			return PreOrder;
		}

		BBOrderList& getDFSPostOrder() {
			return PostOrder;
		}

		BBOrderList& getDFSReversePostOrder() {
			return ReversePostOrder;
		}

		TimeStamp& getBlockTS(BBTy* BB) {
			return DfsTS(BB);
		}

	};

参考资料：

1. 反编译与软件逆向分析。
2. 数据流分析与实践。
3. 高级编译器设计与实现。

（由于博主水平有限，如有讲述错误之处，请留言指正。）