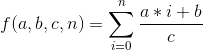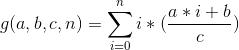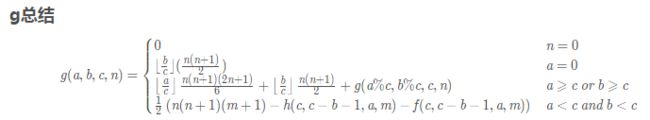这个算法和欧几里得并无直接联系,它是一个完完全全的新算法,我们省略推导过程,直接记录结论。
首先,我们有如下定义:
注意:接下来出现的出发均为向下取整!
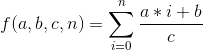
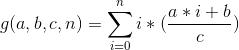


对于上面这三个式子,我们分别有
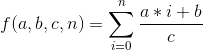
当a>=c or b>=c的时候,我们有

当a

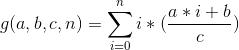
当a>=c or b>=c的时候,我们有

当a
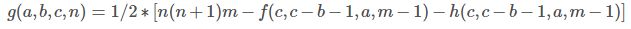

当a>=c or b>=c的时候,我们有

当a

概括一下,就是


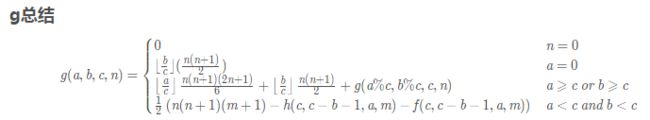
f还有一个单独的模板:
int S1(int n){return n*(n+1)/2;}
int f(int a,int b,int c,int n){
if(!n) return b/c;
if(!a) return (n+1)*(b/c);
if(a>=c||b>=c)return S1(n)*(a/c)+n*(b/c)+f(a%c,b%c,c,n);
return n*((a*n+b)/c)-f(c,c-b-1,a,(a*n+b)/c-1);
}
附上一道例题:https://ac.nowcoder.com/acm/contest/889/i
直接上AC代码,不懂去看 https://blog.csdn.net/xiaobian_/article/details/99685075
#include
using namespace std;
typedef unsigned long long ull;
typedef __int128 ll;
const int mod = 1e9+7;
ll f(ll a, ll b, ll c, ll n){
if(a == 0)
return (n+1) * (b/c);
if(a < c && b < c){
ll m = (a*n+b)/c;
if(m == 0)
return 0;
return n*m - f(c, c-b-1, a, m-1);
}
return f(a%c, b%c, c, n) + (n+1)*(b/c) + (n+1)*n/2*(a/c);
}
ll n, m, ans;
ull x, y;
int res;
int main(){
scanf("%llu%llu", &x, &y);
n = x, m = y;
for(ll i = 1; i <= n*m; i += i)
if(m & i)
ans += (f(m, m, i, n-1)%mod - f(m, m, i+i, n-1)*2%mod + mod)*i % mod;
res = ans % mod;
printf("%d\n", res);
return 0;
}
洛谷模板题目: https://www.luogu.org/problem/P5170
#include
#include
#include
#define ll long long
using namespace std;
const ll Mod=998244353;
const ll inv2=499122177,inv6=166374059;
ll S1(ll x){if(x>=Mod)x%=Mod;return (x*(x+1)%Mod)*inv2%Mod;}
ll S2(ll x){if(x>=Mod)x%=Mod;return (x*(x+1)%Mod*(x+x+1)%Mod)*inv6%Mod;}
ll Sqr(ll x){return x*x%Mod;}
struct node{
ll f,g,h;
void clear(){f=g=h=0;}
node(){}
node(ll a,ll b,ll c):f(a),g(b),h(c){}
void out(){printf("%lld %lld %lld\n",f,g,h);}
};
node calc(ll a,ll b,ll c,ll n){
node ans,res;ans.clear();
ll m,t1,t2,s1,s2;
if(!n){ans.f=b/c;ans.g=Sqr(b/c);return ans;}
if(!a){
t1=b/c;
ans.f=(n+1ll)*t1%Mod;
ans.g=(n+1ll)*Sqr(t1)%Mod;
ans.h=S1(n)*t1%Mod;
return ans;
}
if(a>=c||b>=c){
t1=a/c;t2=b/c;
res=calc(a%c,b%c,c,n);
s1=S1(n);s2=S2(n);
ans.f=(((s1*t1%Mod)+(n+1ll)*t2%Mod)%Mod+res.f)%Mod;
ans.g=(((Sqr(t1)*s2%Mod+(n+1ll)*Sqr(t2)%Mod)%Mod)+((t1*t2%Mod)*2ll*s1%Mod+(t1*2ll*res.h%Mod))%Mod+(res.g+t2*2ll*res.f%Mod)%Mod)%Mod;
ans.h=((s2*t1%Mod+s1*t2%Mod)+res.h)%Mod;
return ans;
}
m=(n*a+b)/c-1;
res=calc(c,c-b-1,a,m);
ll w1=n*(m+1)%Mod,w2=n*(n+1)%Mod,w3=m+1;
if(w3>=Mod)w3%=Mod;
ans.f=(w1-res.f)%Mod;if(ans.f<0)ans.f+=Mod;
ans.g=((w1*w3)%Mod-((res.h*2ll%Mod+res.f)%Mod))%Mod;if(ans.g<0)ans.g+=Mod;
ans.h=((w2*w3)%Mod-(res.f+res.g)%Mod)%Mod*inv2%Mod;if(ans.h<0)ans.h+=Mod;
return ans;
}
int a,b,c,n,T;
int main(){
for(scanf("%d",&T);T--;){scanf("%d%d%d%d",&n,&a,&b,&c);calc(a,b,c,n).out();}
return 0;
}
公式模板来自: https://blog.csdn.net/VictoryCzt/article/details/86099938?utm_source=app
![]()
![]()
![]()
![]()
![]()
![]()