Tree Queries
You are given a rooted tree consisting of n vertices numbered from 1 to n. The root of the tree is a vertex number 1.
A tree is a connected undirected graph with n−1 edges.
You are given m queries. The i-th query consists of the set of ki distinct vertices vi[1],vi[2],…,vi[ki]. Your task is to say if there is a path from the root to some vertex u such that each of the given k vertices is either belongs to this path or has the distance 1 to some vertex of this path.
Input
The first line of the input contains two integers n and m (2≤n≤2⋅105, 1≤m≤2⋅105) — the number of vertices in the tree and the number of queries.
Each of the next n−1 lines describes an edge of the tree. Edge i is denoted by two integers ui and vi, the labels of vertices it connects (1≤ui,vi≤n,ui≠vi).
It is guaranteed that the given edges form a tree.
The next m lines describe queries. The i-th line describes the i-th query and starts with the integer ki (1≤ki≤n) — the number of vertices in the current query. Then ki integers follow: vi[1],vi[2],…,vi[ki] (1≤vi[j]≤n), where vi[j] is the j-th vertex of the i-th query.
It is guaranteed that all vertices in a single query are distinct.
It is guaranteed that the sum of ki does not exceed 2⋅105 (∑i=1mki≤2⋅105).
Output
For each query, print the answer — “YES”, if there is a path from the root to some vertex u such that each of the given k vertices is either belongs to this path or has the distance 1 to some vertex of this path and “NO” otherwise.
Example
input
10 6
1 2
1 3
1 4
2 5
2 6
3 7
7 8
7 9
9 10
4 3 8 9 10
3 2 4 6
3 2 1 5
3 4 8 2
2 6 10
3 5 4 7
output
YES
YES
YES
YES
NO
NO
Note
The picture corresponding to the example:
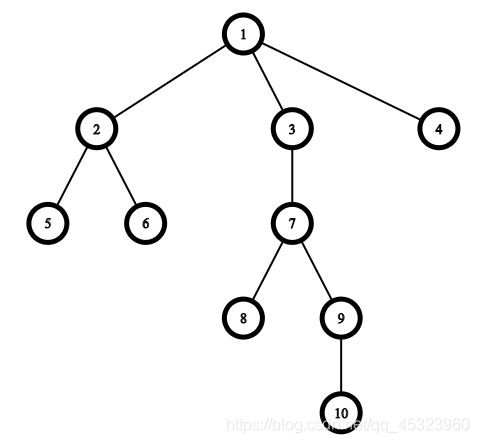
Consider the queries.
The first query is [3,8,9,10]. The answer is “YES” as you can choose the path from the root 1 to the vertex u=10. Then vertices [3,9,10] belong to the path from 1 to 10 and the vertex 8 has distance 1 to the vertex 7 which also belongs to this path.
The second query is [2,4,6]. The answer is “YES” as you can choose the path to the vertex u=2. Then the vertex 4 has distance 1 to the vertex 1 which belongs to this path and the vertex 6 has distance 1 to the vertex 2 which belongs to this path.
The third query is [2,1,5]. The answer is “YES” as you can choose the path to the vertex u=5 and all vertices of the query belong to this path.
The fourth query is [4,8,2]. The answer is “YES” as you can choose the path to the vertex u=9 so vertices 2 and 4 both have distance 1 to the vertex 1 which belongs to this path and the vertex 8 has distance 1 to the vertex 7 which belongs to this path.
The fifth and the sixth queries both have answer “NO” because you cannot choose suitable vertex u.
找到所给集合中深度最深的点,然后与集合中的其他点求lca,判断lca是否是其他点或其他点的父节点,由于树链可能不是从1出发,因此将不满足条件的点放在一起再判断一遍。
#include
using namespace std;
inline int qr() {
int f = 0, fu = 1;
char c = getchar();
while (c < '0' || c > '9') {
if (c == '-')fu = -1;
c = getchar();
}
while (c >= '0' && c <= '9') {
f = (f << 3) + (f << 1) + c - 48;
c = getchar();
}
return f * fu;
}
const int N = 2e5 + 10;
int n, m, head[N], ver[N << 1], Next[N << 1], tot;
int f[N][20], d[N], t;
vi st, ote;
inline void add(int x, int y) {
ver[++tot] = y;
Next[tot] = head[x];
head[x] = tot;
}
inline void read() {
n = qr(), m = qr();
repi(i, 1, n - 1) {
int x = qr(), y = qr();
add(x, y), add(y, x);
}
}
inline void bfs() {
t = (int) log2(n) + 1;
queue<int> q;
d[1] = 1;
q.push(1);
while (!q.empty()) {
int x = q.front();
q.pop();
reps(x) {
int y = ver[i];
if (d[y])continue;
d[y] = d[x] + 1, f[y][0] = x;
repi(j, 1, t)f[y][j] = f[f[y][j - 1]][j - 1];
q.push(y);
}
}
}
inline int lca(int x, int y) {
if (d[x] > d[y])swap(x, y);
repd(i, t, 0)if (d[f[y][i]] >= d[x])y = f[y][i];
if (x == y)return x;
repd(i, t, 0)if (f[x][i] != f[y][i])
x = f[x][i], y = f[y][i];
return f[x][0];
}
inline void solve() {
while (m--) {
int k = qr();
st.clear();
repi(i, 1, k) {
int x = qr();
st.pb(x);
}
int mxi = 0;
for (auto i:st)if (d[i] > d[mxi])mxi = i;
ote.clear();
int cnt = 1;
for (auto i:st) {
if (i == mxi)continue;
int lc = lca(mxi, i);
if (lc == i || lc == f[i][0])cnt++;
else ote.pb(i);
}
mxi = 0;
for (auto i:ote)if (d[i] > d[mxi])mxi = i;
for (auto i:ote) {
if (i == mxi)continue;
int lc = lca(mxi, i);
if (lc == i || lc == f[i][0])cnt++;
}
puts(cnt == k ? "YES" : "NO");
}
}
int main() {
read();
bfs();
solve();
return 0;
}