numpy常用知识整理
1、numpy生成常见概率分布
二项分布
试验由一系列相同的n个试验组成,每次试验有两种可能的结果,成功或者失败;每次试验成功的概率是相同的,用p来表示;试验是相互独立的。
设x为n次试验中的成功的次数,由于随机变量的个数是有限的,所以x是一个离散型随机变量
import numpy as np
import matplotlib.pyplot as plt
n=100
p=0.7
a = np.random.binomial(n, p, size=10000)
#绘制柱状图,bins是柱数
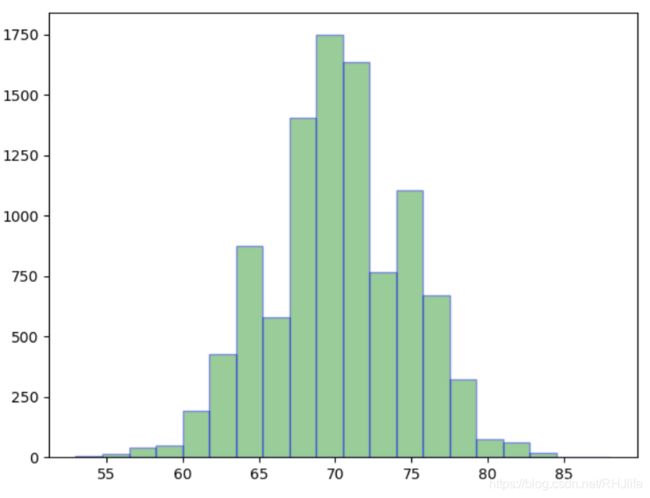
plt.hist(a,bins=20,color='g',alpha=0.4,edgecolor='b')
plt.show()每次进行一百次,概率是0.7所以大概70左右是最多的,剩下的依次递减(理论和图像也比较接近)
泊松分布
在任意两个相等长度的区间上,事件发生的概率相等;事件在某一区间上是否发生与事件在其他区间上是否发生所独立的。
设一个某站台平均每小时会经过8辆公共汽车
import numpy as np
import matplotlib.pyplot as plt
b = np.random.poisson(8,1000)#试验重复1000次
plt.hist(b,bins=16,color='g',alpha=0.4,edgecolor='b')
#输出坐标轴
print(plt.hist(b,bins=16,color='g',alpha=0.4,edgecolor='b'))
plt.show()输出坐标轴的数值
通过上图可以求解各个时间段经过x辆车的概率(例如求每小时经过15辆的概率,因为进行了1000次,所以图片中x=15对应的y/1000即所求概率)
均匀分布
在任意相同长度间隔内分布概率相等的概率分布
low为下限,high为上限,size为取样数量
import numpy as np
import matplotlib.pyplot as plt
low=-1
high=1
size=100000
c=np.random.uniform(low,high,size)
#输出坐标轴
print(plt.hist(c,bins=16,color='g',alpha=0.4,edgecolor='b'))
plt.show()在这个区间内的生成的数基本持平(size越大则越准确)
正态分布
当二项分布的样本数量足够大时,其分布曲线会变成对称的钟形,我们将这种分布形态成为正态分布
loc为期望,scale为标准差,size为取样数量,默认为Non
import numpy as np
import matplotlib.pyplot as plt
d = np.random.normal(loc=0,scale=1,size=100000)
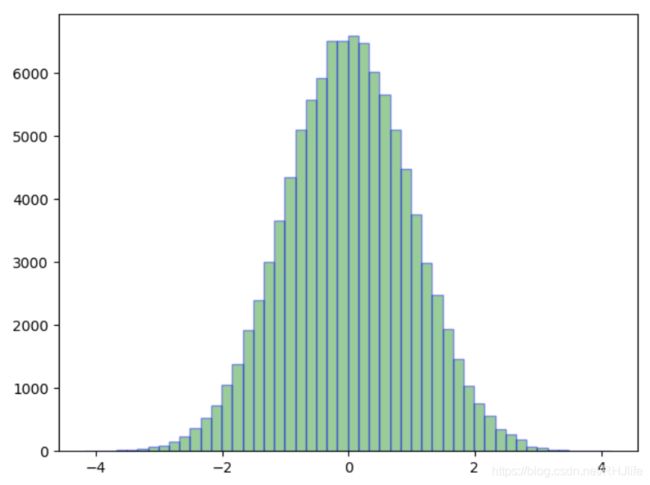
plt.hist(d,bins=50,color='g',alpha=0.4,edgecolor='b')
plt.show()指数分布
指数分布与泊松分布类似,泊松分布描述了每一个区间内事件发生的次数,而指数分布描述了事件发生的事件间隔长度。
设一个某站台平均每小时会经过8辆公共汽车,可以求两辆公共汽车间隔时间不超过x小时的概率
参数根据题目应该好了解~
import numpy as np
import matplotlib.pyplot as plt
e = np.random.exponential(1/8,10000)
plt.hist(e,bins=20,color='g',edgecolor='b',alpha=0.4)
plt.show()概率求解与泊松分布类似
2、numpy生成各类随机数
import numpy as np
import matplotlib.pyplot as plt
#0-10范围内的整数,100个
a=np.random.randint(0,10,100)
print(a)
##0到1的均匀分布,40个
b=np.random.rand(40)
print(b)
##标准正态分布,10个
c=np.random.randn(10)
print(c)
#生成指定正态分布,均值0。方差1,100个
d=np.random.normal(0,1,100)
print(d)
#0到1的均匀分布,20个
e=np.random.random(20)
print(e)
#0到1的均匀分布。20个
f=np.random.ranf(20)
print(f)
#指定-1到1均匀分布,100个
g=np.random.uniform(-1,1,100)
print(g)