模拟赛:NOIP2015题解(day2)
这两天打了一次NOIP2015day2,才得了140分…第二题空间开爆了…
T1 河中跳石头
【问题描述】一年一度的“跳石头”比赛又要开始了!这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有N块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走M块岩石(不能移走起点和终点的岩石)。
没啥说的,NOI题库,二分答案直接判断
Code
#includeT2 子串 substring
题目描述
有两个仅包含小写英文字母的字符串 A 和 B。
现在要从字符串 A 中取出 k 个互不重叠的非空子串,然后把这 k 个子串按照其在字符串 A 中出现的顺序依次连接起来得到一个新的字符串。请问有多少种方案可以使得这个新串与字符串 B 相等?
注意:子串取出的位置不同也认为是不同的方案。
输入输出格式
输入格式:
第一行是三个正整数 n,m,k,分别表示字符串 A 的长度,字符串 B 的长度,以及问题描述中所提到的 k,每两个整数之间用一个空格隔开。
第二行包含一个长度为 nn 的字符串,表示字符串 A。
第三行包含一个长度为 mm 的字符串,表示字符串B。
输出格式:
一整数,表示所求方案数。
由于答案可能很大,所以这里要求输出答案对 1000000007 取模的结果。
输入输出样例
输入样例#1:
6 3 1
aabaab
aab
输出样例#1:
2
输入样例#2:
6 3 2
aabaab
aab
输出样例#2:
7
输入样例#3:
6 3 3
aabaab
aab
输出样例#3:
7
说明
对于第 1 组数据:1≤n≤500,1≤m≤50,k=1;
对于第 2 组至第 3 组数据:1≤n≤500,1≤m≤50,k=2;
对于第 4 组至第 5 组数据:1≤n≤500,1≤m≤50,k=m;
对于第 1 组至第 7 组数据:1≤n≤500,1≤m≤50,1≤k≤m;
对于第 1 组至第 9 组数据:1≤n≤1000,1≤m≤100,1≤k≤m;
对于所有 10 组数据:1≤n≤1000,1≤m≤2001≤k≤m。
这道题,一道不错的dp
我们考虑设f[i][j][k]来表示A串的前i个匹配B串的前j个用了A的k个子串的方案数
易得
f [ i ] [ j ] [ k ] = f [ i − 1 ] [ j ] [ k ] , a [ i ] ! = b [ j ] f[i][j][k]=f[i-1][j][k] ,a[i]!=b[j] f[i][j][k]=f[i−1][j][k],a[i]!=b[j]
关键在于当a[i]==b[j]时,我们无法判断最后一个子串延伸到哪里
我们可以引入一个新的状态:g[i][j][k]表示A串的前i个匹配B串的前j个用了A的k个子串,且a[i]包含于最后一个子串的方案数
这样状态就好表示啦
f [ i ] [ j ] [ k ] = { f [ i − 1 ] [ j ] [ k ] a [ i ] ! = b [ j ] f [ i − 1 ] [ j ] [ k ] + f [ i − 1 ] [ j − 1 ] [ k − 1 ] + g [ i − 1 ] [ j − 1 ] [ k ] a [ i ] = = b [ j ] f[i][j][k]=\begin{cases} f[i-1][j][k] & a[i]!=b[j] & \\ f[i-1][j][k]+f[i-1][j-1][k-1]+g[i-1][j-1][k] & a[i]==b[j] \\ \end{cases} f[i][j][k]={f[i−1][j][k]f[i−1][j][k]+f[i−1][j−1][k−1]+g[i−1][j−1][k]a[i]!=b[j]a[i]==b[j]
g [ i ] [ j ] [ k ] = { 0 a [ i ] ! = b [ j ] f [ i − 1 ] [ j − 1 ] [ k − 1 ] + g [ i − 1 ] [ j − 1 ] [ k ] a [ i ] = = b [ j ] g[i][j][k]=\begin{cases} 0 & a[i]!=b[j] & \\ f[i-1][j-1][k-1]+g[i-1][j-1][k] & a[i]==b[j] \\ \end{cases} g[i][j][k]={0f[i−1][j−1][k−1]+g[i−1][j−1][k]a[i]!=b[j]a[i]==b[j]
但是!!!!由于这道上古题空间只有128mb,我们开的空间太大,需要滚动数组
CODE
#include
}
}
}
printf("%d",f[n&1][m][k]%mod);
return 0;
}
T3 运输计划
.
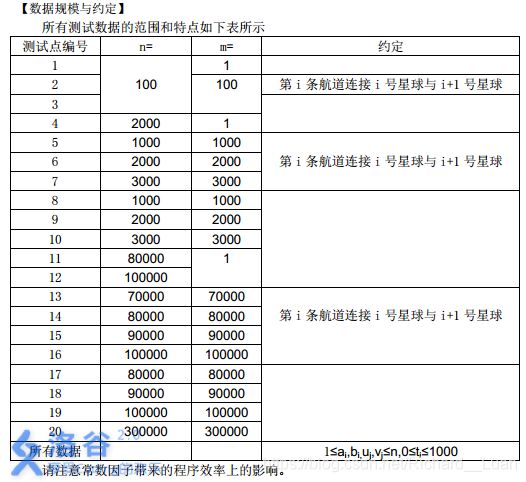
【问题描述】公元2044年,人类进入了宇宙纪元。L国有n个星球,还有n-1条双向航道,每条航道建立在两个星球之间,这n-1条航道连通了L国的所有星球。小P掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物流飞船需要从ui号星球沿最快的宇航路径飞行到vi号星球去。显然,飞船驶过一条航道是需要时间的,对于航道j,任意飞船驶过它所花费的时间为tj,并且任意两艘飞船之间不会产生任何干扰。为了鼓励科技创新,L国国王同意小P的物流公司参与L国的航道建设,即允许小P把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。在虫洞的建设完成前小P的物流公司就预接了m个运输计划。在虫洞建设完成后,这m个运输计划会同时开始,所有飞船一起出发。当这m个运输计划都完成时,小P的物流公司的阶段性工作就完成了。如果小P可以自由选择将哪一条航道改造成虫洞,试求出小P的物流公司完成阶段性工作所需要的最短时间是多少?
输入输出格式
输入格式:
第一行包括两个正整数 n,m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。
接下来 n−1 行描述航道的建设情况,其中第 i 行包含三个整数 a i , b i , 和 t i a_i, b_i, 和 t_i ai,bi,和ti,表示第 i 条双向航道修建在 a i a_i ai与 b i b_i bi 两个星球之间,任意飞船驶过它所花费的时间为 t i t_i ti。数据保证 1 ≤ a i , b i ≤ n 1 ≤ a i , b i ≤ n 1 ≤ a i , b i ≤ n 且 0 ≤ t i ≤ 10000 ≤ t i ≤ 10000 ≤ t i ≤ 1000 1≤ai,bi≤n1 \leq a_i,b_i \leq n1≤ai,bi≤n 且 0≤ti≤10000 \leq t_i \leq 10000≤ti≤1000 1≤ai,bi≤n1≤ai,bi≤n1≤ai,bi≤n且0≤ti≤10000≤ti≤10000≤ti≤1000
接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j 个运输计划是从 uj 号星球飞往 vj号星球。数据保证 1 ≤ u i , v i ≤ n 1 ≤ u i , v i ≤ n 1 ≤ u i , v i ≤ n 1≤ui,vi≤n1 \leq u_i,v_i \leq n1≤ui,vi≤n 1≤ui,vi≤n1≤ui,vi≤n1≤ui,vi≤n
输出格式:
一个整数,表示小 P 的物流公司完成阶段性工作所需要的最短时间。
输入输出样例
输入样例#1:
6 3
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5
输出样例#1:
11
说明
这道题思路还是比较自然,我考场上码了200来行写了40分
首先由问题提示得知用二分求解,只需贪心求所有路径长度大于mid的链中共同的链中最长的链即可
问题转化为求几个链的交集
我考场上暴力合啊啊啊
实际只需做一次树上差分,求tag即可
Code(85)
不知道错哪了,懒得改了
#include
if(!num[x])
{
num[x]=++cnt;
reuler[cnt]=x;
pos[x]=tot+1;
}
euler[++tot]=num[x];
for(int i=fst[x];i;i=nxt[i])
{
if(v[i]!=pre)
{
dep[v[i]]=dep[x]+k[i];
dp[v[i]]=dp[x]+1;
fa[v[i]]=x;
dfs(v[i],x);
euler[++tot]=num[x];
}
}
}
int lca(int x,int y)
{
x=pos[x];
y=pos[y];
//cout<
if(x>y)swap(x,y);
return reuler[min(minn[x][lg[y-x+1]],minn[y-(1<<(lg[y-x+1]))+1][lg[y-x+1]])];
}
struct poi
{
int x, y, len;
//poi(int x,int y,int len):x(x),y(y),len(len){}
}c[maxn];
poi make_poi(int x,int y,int len)
{
poi re;
re.x=x;
re.y=y;
re.len=len;
return re;
}
bool cmp(poi a,poi b)
{
return a.len>b.len;
}
int tag[maxn];
int dfs2(int x,int pre,int num)
{
int maxx=-1;
// cout<
for(int i=fst[x];i;i=nxt[i])
{
if(v[i]!=pre)
{
maxx=max(maxx,dfs2(v[i],x,num));
//if(tag[v[i]]>num)cout<
if(tag[v[i]]>=num)maxx=max(maxx,k[i]);
tag[x]+=tag[v[i]];
// if(tag[x]>num)cout<
}
}
//cout<
return maxx;
}
bool check(int x)
{
//cout<<"----------------------"<
//cout<
memset(tag,0,sizeof(tag));
if(c[1].len<=x)return 1;
for(int i=1;i<=m;i++)
{
if(c[i].len<=x)
{
//cout<
if(c[1].len-dfs2(1,-1,i-1)<=x)return 1;
return 0;
}
tag[c[i].x]++;
tag[c[i].y]++;
tag[lca(c[i].x,c[i].y)]-=2;
// cout<
}
return c[1].len-dfs2(1,-1,m)<=x;
}
int main()
{
//freopen("transport.in","r",stdin);
//freopen("transport.out","w",stdout);
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++)
{
int x,y,val;
scanf("%d%d%d",&x,&y,&val);
add(x,y,val);
add(y,x,val);
}
dfs(1,-1);
for(int i=1;i<=tot;i++)
{
minn[i][0]=euler[i];
}
for(int i=2;i<=tot;i++)
lg[i]=lg[i>>1]+1;
for(int j=1;j<=20;j++)
{
for(int i=1;i<=tot;i++)
{
minn[i][j]=min(minn[i][j-1],minn[min(tot,i+(1<<(j-1)))][j-1]);
}
}
int maxx=-1;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&c[i].x,&c[i].y);
c[i].len=dep[c[i].x]+dep[c[i].y]-2*dep[lca(c[i].x,c[i].y)];
maxx=max(maxx,c[i].len);
}
sort(c+1,c+1+m,cmp);
int l=0,r=maxx+1;
while(l<r-1)
{
int mid=l+r>>1;
if(check(mid))r=mid;
else l=mid;
}
if(check(l))printf("%d",l);
else printf("%d",r);
return 0;
}