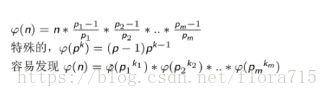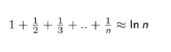【暖*墟】 #洛谷省选网课# 8.1数论进阶
目录
一. 整除 取整除法
二. 因子 唯一分解定理
三. 同余系与剩余系
1.同余的概念和性质
2.剩余系与剩余定理
3.裴蜀定理
4.乘法逆元
5.1 费马小定理与欧拉定理
5.2 欧拉函数
5.3 积性函数的性质和应用
四. 质数
五. 公约数
1.欧几里得算法
2.互质的概念与性质
六. 阶的定义与性质
七. 原根
八. 调和级数
九. 莫比乌斯函数
【1.狄利克雷卷积】
性质1 》 性质2 》 性质3 》 性质4 》
Q: 求狄利克雷卷积前n项?
【2.莫比乌斯反演 ppt学习】
例题 - luogu2257 YY的GCD
例题 - SDOI2014 数表(table)
【 3.杜教筛】
数论中最重要的函数:欧拉函数和莫比乌斯函数。
一. 整除
取整除法
取整除法求和
(找不到之前的证明了...先留个坑)
二. 因子
- 平凡因子:1和自身。
- 若p是质数,则p没有非平凡因子。
- 若p没有非平凡因子,则p是质数。
唯一分解定理
三. 同余系与剩余系
1.同余的概念和性质
2.剩余系与剩余定理
???
3.裴蜀定理
4.乘法逆元
5.1 费马小定理与欧拉定理
5.2 欧拉函数
5.3 积性函数的性质和应用
f(ab)=f(a)*f(b) 可用于分解因式求函数值。
四. 质数密度
五. 公约数
1.欧几里得算法
2.互质的概念与性质
3.扩展欧几里得算法
a、线性同余
线性同余方程(也可以叫模线性方程)是最基本的同余方程,即ax≡b (mod n),
其中a、b、n都为常量,x是未知数,一定的转化后得到:ax = kn + b,
这里的k为任意整数,于是我们可以得到更加一般的形式即:ax + by + c = 0,
这个方程就是二维空间中的直线方程,但是x和y的取值为整数,
所以这个方程的解是一些排列成直线的点集。
b、同余方程求解
求解同余方程第一步是转化成一般式:ax + by = c,这个方程的求解步骤如下:
- 首先求出a和b的最大公约数d = gcd(a, b),那么原方程可以转化成d(ax/d + by/d) = c,
- 容易知道(ax/d + by/d)为整数,如若d不能整除b,方程必然无解,算法结束;否则进入 ii 。
- 由 i 可以得知,方程有解则一定可以表示成 ax + by = c = gcd(a, b)*c’,
- 那么我们先来看如何求解d = gcd(a, b) = ax + by,根据欧几里德定理,
- 有:d = gcd(a, b) = gcd(b, a%b) = bx’ + (a%b)y’ = bx’ + [a-b*(a/b)]y’ = ay’ + b[x' - (a/b)y'],
- 于是有x = y’, y = x’ – (a/b)y’。
由于gcd(a, b)是一个递归的计算,所以在求解(x, y)时,
(x’, y’)其实已经利用递归计算出来了,递归出口为b == 0的时候,
(对比辗转相除,也是b == 0的时候递归结束),那么这时方程的解x0 = 1, y0 = 0。
代码如下:
#define LL __int64
LL Extend_Euclid(LL a, LL b, LL &X, LL &Y) {
LL q, temp;
if( !b ) {
X = 1; Y = 0;
return a;
}else {
q = Extend_Euclid(b, a % b, X, Y);
temp = X; X = Y;
Y = temp - (a / b) * Y;
return q;
}
}扩展欧几里德算法和欧几里德算法的返回值一致,都是gcd(a, b),
传参多了两个未知数X, Y,采用引用的形式进行传递,对应上文提到的x, y,
递归出口为b == 0,这时返回值为当前的a,因为gcd(a, 0) = a,
(X, Y)初值为(1, 0),然后经过回溯不断计算新的(X, Y)。
这个计算是利用了之前的(X, Y)进行迭代计算的,直到回溯到最上层算法终止。
最后得到的(X, Y)就是方程gcd(a, b) = ax + by的解。
- 通过扩展欧几里德求的是ax + by = gcd(a, b)的解,令解为(x0, y0),
- 代入原方程,得:ax0 + by0 = gcd(a, b),如果要求ax + by = c = gcd(a, b)*c’,
- 可以将上式代入,得:ax + by = c = (ax0 + by0)c’,则x = x0c’, y = y0c’,
- 这里的(x, y)只是这个方程的其中一组解,
- x的通解为 { x0c’ + kb/gcd(a, b) | k为任意整数 },
- y的通解可以通过x通解的代入得出。
六. 阶的定义与性质
1.阶的定义:
(a,m)=1,则最小的正整数r使得a^r=1(mod m) 为a模m的阶。
2.阶的性质:
r | φ(m) 。(可用反证法,假设不整除,则……)
3.求阶:
给定互质的a,m,求a模m的阶?
4.原根定义:
若a模m的原根为φ(m),则a为m的一个原根。
5.原根性质:
特别注意:只有m=2,4,p^a,2·p^a时m才有原根(p为奇素数,a≥1)
6.求原根:
首先需要判断一下m是否存在原根(程序中略去,且m仍为奇素数);
然后从2开始枚举每一个与m互质的数,看他模m的阶是否等于φ(m)。
充要条件是:对于正在枚举的i,和φ(m)的每一个不同的质因子p:
都有 i^( φ(m)/p )mod m≠1,则i就是m的一个原根! (m的质因数需要预处理出来)
一般原根都会很小,时间复杂度可以理解为O(√m+k·log(m)^2),√m为预处理,k为检验的次数
经测试:10000000以内的数只有:
6252122 101
6497402 115
6933362 113
7871018 101
程序中vis[ ]是线性筛素数的bool数组,vis[i]=1表示i非素数。
int pow(int x,int y,int p){
int ret=1,now=x;
for(;y;y>>=1,now=1ll*now*now%p)
if(y&1)ret=1ll*ret*now%p;
return ret;
}
int Find_Root(int m,int phi_m)//if m has no root,then return 0
{
if(vis[m]&&(m%2==1||vis[m/2]))return 0;
int cnt=0,lim=int(sqrt(phi_m)),now=phi_m;
for(int i=2;i<=lim;i++)
if(now%i==0){
tempri[++cnt]=i;
while(!(now%i))now/=i;
} if(now>1)tempri[++cnt]=now;
for(int i=1;;i++){
bool flag=1;
for(int j=1;j<=cnt;j++)
if(pow(i,phi_m/tempri[j],m)<=1){flag=0;break;}
if(flag&&pow(i,phi_m,m)==1)return i;
}
return 0;
}
七. 原根
![]()
八. 调和级数
通常用于判断时间复杂度。
九. 莫比乌斯函数
理解:如果有平方因子,值为0。如果因数个数为奇数(偶数),值为-1(1)。
莫比乌斯函数最重要的应用:(某因数下的求和)
若d是n的因子,且 u(d)!=0时,d是n0的因子。
n0是n的因子,则原式中有了一个平方项。
↑↑↑ 因数下函数求和之间的关系。
mu函数的求法:
void Linear_Shaker(int n){
mu[1] = 1;
for (int i = 2; i <= n; i++){
if (!ism[i]) {prm[++tot] = i; mu[i] = -1;}
for (int j = 1; j <= tot; j++){
int num = prm[j] * i;
if (num > n) break;
ism[num] = 1;
if (i % prm[j] == 0) break;
mu[num] = -mu[i];
}
}
}
狄利克雷卷积
性质1 》
两个函数的*是卷积,两个数字的*是乘号。
性质2 》
g(n)是n所有因子的f函数的值之和
↑↑↑这里的1是一个常数函数
性质3 》
性质4 》
两个积性函数的狄利克雷卷积也是积性函数。
两个例子:欧拉函数φ和莫比乌斯函数μ。
都可以用线性筛法求出。
Q: 求狄利克雷卷积前n项?
↑↑↑可以用暴力的方法直接得出 (???)
莫比乌斯反演 ppt学习
有数论函数f, g。
其中 μ是莫比乌斯函数:
显然:莫比乌斯函数的逆元
根据定义即可得出莫比乌斯函数的逆元(逆函数) 为 1 。
这样,莫比乌斯反演就可以证明了:因为
写成狄利克雷卷积的形式就是:
即可得到:
展开来写也就是:
运用简单的换元小法术,即可得到莫比乌斯反演的结论:
例题 - luogu2257 YY的GCD
具体分析:
代码实现:
#include
#define N 10000100
using namespace std;
inline void read(int &x){
x=0;
static int p;p=1;
static char c;c=getchar();
while(!isdigit(c)){if(c=='-')p=-1;c=getchar();}
while(isdigit(c)) {x=(x<<1)+(x<<3)+(c-48);c=getchar();}
x*=p;
}
inline void print(long long x){
static int cnt;
static int a[15];
cnt=0;
do{
a[++cnt]=x%10;
x/=10;
}while(x);
for(int i=cnt;i>=1;i--)putchar(a[i]+'0');
puts("");
}
bool vis[N];
long long sum[N];
int prim[N];
int mu[N],g[N];
int cnt;
void get_mu(int n){
mu[1]=1;
for(int i=2;i<=n;i++){
if(!vis[i]){mu[i]=-1;prim[++cnt]=i;}
for(int j=1;j<=cnt&&prim[j]*i<=n;j++){
vis[i*prim[j]]=1;
if(i%prim[j]==0)break;
else mu[prim[j]*i]=-mu[i];
}
}
for(int j=1;j<=cnt;j++)
for(int i=1;i*prim[j]<=n;i++)g[i*prim[j]]+=mu[i];
for(int i=1;i<=n;i++)sum[i]=sum[i-1]+(long long)g[i];
}
int n,m;
int main(){
#ifndef ONLINE_JUDGE
freopen("P2257.in","r",stdin);
freopen("P2257.out","w",stdout);
#endif
int t;
read(t);
get_mu(10000000);
while(t--){
read(n);read(m);
if(n>m)swap(n,m);
static long long ans;ans=0;
for(int l=1,r;l<=n;l=r+1){
r=min(n/(n/l),m/(m/l));
ans+=1ll*(n/l)*(m/l)*(sum[r]-sum[l-1]);
}
print(ans);
}
return 0;
}
例题 -【SDOI2014】数表(table)
#include
#include
#include
#include
#include
using namespace std;
#define fo(i,a,b) for(i=a;i<=b;i++)
const int maxn=1e5+5;
typedef long long ll;
struct arr{
int n,m,mx,bh;
}a[20005];
struct da{
int f,pr;
}f[maxn];
bool cmp(arr x,arr y){return x.mxmx) break;
p[k]=true;
if(i%s[j]==0){
mu[k]=0;
break;
}
mu[k]=mu[i]*mu[s[j]];
}
}
mu[1]=1;
fo(i,1,mx){
f[i].pr=i;
for(j=i;j<=mx;j+=i) f[j].f+=i;
}
}
void add(int x,int sum){
for(x=x;x<=mx;x+=x&(-x)) t[x]+=sum;
}
int get(int x){
int sum;
sum=0;if(x==0) return 0;
for(x=x;x;x-=x&(-x)) sum+=t[x];
return sum;
}
void solve(int x)
{
int n,m,bh,i,j;
n=a[x].n,m=a[x].m,bh=a[x].bh;
for(i=1;i<=n;i=j+1){
j=min(n/(n/i),m/(m/i));
ans[bh]+=(n/i)*(m/i)*(get(j)-get(i-1));
}
}
int main(){
freopen("table.in","r",stdin);
freopen("table.out","w",stdout);
mo=1;fo(i,1,31) mo=mo*2;
scanf("%d",&cas);
fo(i,1,cas){
scanf("%d%d%d",&a[i].n,&a[i].m,&a[i].mx);
if(a[i].n>a[i].m) swap(a[i].n,a[i].m);
a[i].bh=i;mx=max(mx,a[i].n);
}
screen(mx);
sort(a+1,a+cas+1,cmp);
sort(f+1,f+mx+1,cmp1);
j=0;
fo(i,1,cas){
while(j
杜教筛
用于欧拉函数和莫比乌斯函数的求和。
( 还有一堆题目见课件... )
——时间划过风的轨迹,那个少年,还在等你。