LeetCode 例题精讲 | 17 动态规划如何拆分子问题，简化思路
在上一篇文章中，我们讲解了「子数组」类动态规划题目的常见技巧。这篇文章继续讲解动态规划问题中的小技巧。今天要讲的是「如何定义多个子问题」。
常规的动态规划问题只需要定义一个子问题即可。然而在某些情况下，把子问题拆成多个会让思路更清晰。如果你没用过这个技巧的话，不妨跟着今天的例题来学习学习。
本篇文章的内容包括：
如何拆分动态规划的子问题
「最长波形子数组」问题的解法
度假问题的解法
多个子问题与二维子问题的转换关系
最长波形子数组
我们用「最长波形子数组」的解题过程来展示定义多个子问题在解题中的作用。
LeetCode 978. Longest Turbulent Subarray 最长波形子数组（Medium）
当
A的子数组A[i..j]满足下列条件之一时，我们称其为波形子数组：对于 i <= k < j，当 k 为奇数时，
A[k] > A[k+1]，当 k 为偶数时，A[k] < A[k+1]；或者：对于 i <= k < j，当 k 为偶数时，
A[k] > A[k+1]，当 k 为奇数时，A[k] < A[k+1]。也就是说，如果比较符号在子数组中的每个相邻元素对之间翻转，则该子数组是波形子数组。
返回 A 的最长波形子数组的长度。
首先我们要明白「波形子数组」的含义。（吐槽一句，官方把 trubulent 翻译成「湍流」，这翻译是给人看的吗？）我们关注的是数组中相邻元素之间的大小关系。如果后一个元素大于前一个元素，则是数组的「上升段」；反之，则是数组的「下降段」。那么，「波形子数组」就是一段交替上升下降的子数组。例如输入 [9, 4, 2, 10, 7, 8, 8, 1, 9] 中， [4, 2, 10, 7, 8] 是其中最长的一段波形子数组。
「波形子数组」是一段交替上升下降的子数组
使用单个子问题求解
我们先看看使用传统的单个子问题该怎么求解这道题。
首先，看到题目中的「子数组」字样，我们应当立即想到子数组相关的解题技巧：在定义子问题的时候给子问题加上位于数组尾部的限制。
不理解这个解题技巧的同学，可以回顾我的上一篇文章：
LeetCode 例题精讲 | 16 最大子数组和：子数组类问题的动态规划技巧
使用这个技巧，我们可以这样定义子问题：
子问题 表示「数组 A[0..k) 中，位于数组尾部的最长波形子数组」。
之所以要限制子问题中求的最长波形子数组位于数组尾部，是因为只有数组尾部的波形子数组才可以和新加入的上升/下降段连接起来。
需要注意的是，波形数组的连接是有条件的，需要「上升段」和「下降段」交替出现。如果波形数组的最后一段是「上升」，就需要连接一段「下降」才是合法的波形数组；而如果波形数组的最后一段是「下降」，就需要连接一段「上升」才是合法的波形数组。
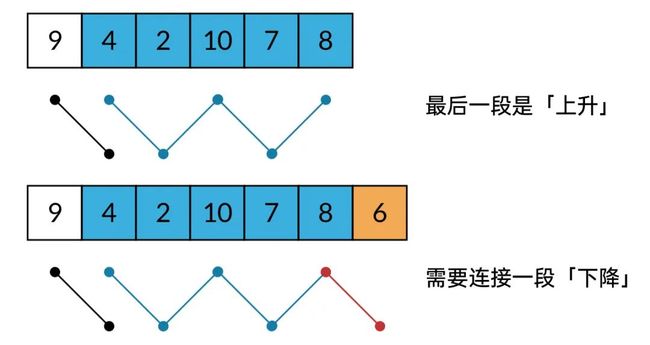如果波形子数组的最后一段是「上升」，就需要连接一段「下降」
而如果「上升」之后又是一段「上升」，那么整个波形数组不合法。波形子数组的长度减少到 2（包含最后一个上升段的两个元素）。
连续两个「上升」段，无法继续连接，长度退化为 2
当然，如果最后一段既不是上升，也不是下降，而是「水平」段，那这最后一段也是不合法的。波形子数组的长度减少到 1。
新加入的是水平段，无法继续连接，长度退化为 1
那么，我们在写子问题的递推关系时，需要分类讨论。对于子问题 ：
如果 波形数组的最后一段是「上升」，且
A[k-1]和A[k-2]之间是「上升」，那么 ；如果 波形数组的最后一段是「上升」，且
A[k-1]和A[k-2]之间是「下降」，那么 ；如果 波形数组的最后一段是「下降」，且
A[k-1]和A[k-2]之间是「上升」，那么 ；如果 波形数组的最后一段是「下降」，且
A[k-1]和A[k-2]之间是「下降」，那么 ；如果
A[k-1]和A[k-2]之间是「水平」，那么 。
什么？一个看似简单的问题竟然要分这么多情况考虑，是不是看得头都大了？
通常来说，如果你发现子问题的递推关系过于复杂，那可能是子问题定义得不是很好。关键的思路来了： 如果对子问题进行拆分，可以减少很多不必要的分类讨论。
下面，我们尝试拆分子问题，使用多个子问题进行求解。
使用多个子问题求解
既然我们总是要判断波形数组的最后一段是上升还是下降，那我们为何不在子问题定义时就把它们区分开来呢？
我们可以定义两个子问题，分别对应最后一段上升和下降的波形子数组：
子问题 表示：数组
A[0..k)中，位于数组尾部，且 最后一段为「上升」 的最长波形子数组；子问题 表示：数组
A[0..k)中，位于数组尾部，且 最后一段为「下降」 的最长波形子数组。
这样一来，我们的子问题递推关系也变得清晰了起来：
如果
A[k-1]和A[k-2]之间是「上升」，那么 ， ；如果
A[k-1]和A[k-2]之间是「下降」，那么 ， ；如果
A[k-1]和A[k-2]之间是「水平」，那么 ， 。
这样，我们就可以写出题解代码了。需要注意的是，既然我们定义了多个子问题，就需要在代码中定义多个 DP 数组。我们直接把 DP 数组命名为 f 和 g，与子问题对应：
public int maxTurbulenceSize(int[] A) {
if (A.length <= 1) {
return A.length;
}
int N = A.length;
// 定义两个 DP 数组 f, g
int[] f = new int[N+1];
int[] g = new int[N+1];
f[0] = 0;
g[0] = 0;
f[1] = 1;
g[1] = 1;
int res = 1;
for (int k = 2; k <= N; k++) {
if (A[k-2] < A[k-1]) {
f[k] = g[k-1] + 1;
g[k] = 1;
} else if (A[k-2] > A[k-1]) {
f[k] = 1;
g[k] = f[k-1] + 1;
} else {
f[k] = 1;
g[k] = 1;
}
res = Math.max(res, f[k]);
res = Math.max(res, g[k]);
}
return res;
}
多个子问题的本质
让我们从 DP 数组的角度来理解动态规划中「定义多个子问题」究竟意味着什么。
请思考一个问题：在「最长波形子数组」问题中，DP 数组是一维的还是二维的？
从子问题的定义来看的话，子问题只有一个参数 ，看起来应该是一维的。不过和普通的一维动态规划问题的不同之处在于，因为有两个子问题 和 ，所以 DP 数组有两个，其中每个是一维的。
我们可以画出 DP 数组的形状来直观地理解。设数组的长度为 ，则 的取值范围是 。DP 数组是两个长度为 的数组，如下图所示。
将 DP 数组看成两个一维的数组
接下来，我们在 DP 数组中画出子问题的依赖关系。 只依赖于 ， 只依赖于 ，那么可以画出子问题的依赖关系为：
DP 数组中子问题的依赖关系
可以看出，两个子问题互相依赖，整体的依赖顺序是从左往右的。
另一方面，我们也可以把 DP 数组看成二维数组。把两个长度为 的数组拼在一起，就得到了一个 的二维数组。
将 DP 数组看成二维数组
但是，这样的一个 DP 数组和常规的二维动态规划中的 DP 数组不太一样：
第一，DP 数组其中一维的长度为 2，是个常数。计算空间复杂度的话，这个二维 DP 数组的空间复杂度是 ，仍然是一维数组的复杂度级别。
第二，一般的二维动态规划问题（如最长公共子序列、编辑距离这些经典题目），DP 数组的计算顺序既可以是从上往下，也可以是从左往右。而这个 DP 数组根据依赖顺序，计算顺序只能是从左往右，不能先计算第一行（ ）再计算第二行（ ）。
DP 数组的计算顺序
综上，我们可以看出，有多个子问题的动态规划，其维度实际上介于一维和二维之间。本题只定义了两个（常数个）子问题，而如果子问题的数量扩展到了 个，DP 数组的空间复杂度就到达了 ，变成了一个真正的二维动态规划问题。
另一道例题：度假问题
让我们再看一道典型的拆分子问题的动态规划题目，来理解定义多个子问题的技巧。这道题不是来自 LeetCode，而是来自另一个算法网站 AtCoder：AtCoder DP-C. Vacation
题目链接：https://atcoder.jp/contests/dp/tasks/dp_c
Taro 的暑假明天开始，他决定现在制定好暑假的计划。
假期共持续 天。Taro 可以选择在第 天（ ）做以下三件事之一：
A：游泳。获得 点快乐指数。
B：捉虫。获得 点快乐指数。
C：写作业。获得 点快乐指数。
由于 Taro 做一件事情很容易无聊，所以他不能连续两天做同一件事情。
输入包括 以及数组 、 、 的内容。
请计算 Taro 总共能获得的最大快乐指数。
这道题目该怎么拆分子问题呢？我们注意到一个关键的题目条件：Taro 不能连续两天做同一件事情。也就是说：
如果 Taro 今天做的是事情 A，那么他明天可以做事情 B 和 C；
如果 Taro 今天做的是事情 B，那么他明天可以做事情 A 和 C；
如果 Taro 今天做的是事情 C，那么他明天可以做事情 A 和 B。
这样的话，我们可以根据 Taro 今天做的是哪件事，定义出三个子问题：
子问题 表示 Taro 在第 k 天做事情 A 的情况下，前 k 天能获得的最大快乐指数；
子问题 表示 Taro 在第 k 天做事情 B 的情况下，前 k 天能获得的最大快乐指数；
子问题 表示 Taro 在第 k 天做事情 C 的情况下，前 k 天能获得的最大快乐指数。
然后我们可以写出子问题间的递推关系：
递推关系为什么是这样的呢？以 的公式为例：
表示表示 Taro 在第 k 天做事情 A 的情况下，前 k 天能获得的最大快乐指数。既然 Taro 在第 k 天做了事情 A，那么他在第 k-1 天就不能做事情 A，只能做事情 B 或 C，对应 和 。也就是说， 是根据 和 求出来的。
和 的公式同理可得。
有了这个递推关系，我们就可以写出题解代码 了：
private static int vacation(int[] a, int[] b, int[] c) {
int n = a.length;
int[] f1 = new int[n+1];
int[] f2 = new int[n+1];
int[] f3 = new int[n+1];
f1[0] = 0;
f2[0] = 0;
f3[0] = 0;
for (int k = 1; k <= n; k++) {
f1[k] = a[k-1] + Math.max(f2[k-1], f3[k-1]);
f2[k] = b[k-1] + Math.max(f1[k-1], f3[k-1]);
f3[k] = c[k-1] + Math.max(f1[k-1], f2[k-1]);
}
return Math.max(f1[n], Math.max(f2[n], f3[n]));
}
可以看到，题解代码还是非常简洁的。在代码中，f1、f2 和 f3 呈现出一种相互依赖、交替计算的关系。
我们可以用这样一张图来描述这三个子问题之间的关系：
三个子问题之间的关系
图中的箭头表示子问题间的依赖关系。例如 到 有一条边，表示 依赖于 。而 不依赖于 ，所以 没有到自己的边。
眼尖的同学可能已经看出，这张图实际上展示的是一个状态机。状态机中有 、 、 三种状态。如果状态机在第 k-1 天位于状态 ，那么第 k 天的状态无法维持在 ，只能跳到 或 。这对应了「Taro 不能连续两天做同一件事情」的题目条件。
实际上，「状态机」是动态规划中的一种技巧，大名鼎鼎的股票买卖问题就是属于「状态机 DP」。下一篇文章会详细介绍股票问题和状态机 DP。
总结
本文用两道例题展示了动态规划问题中拆解子问题、定义多个子问题的技巧。两道题目虽然分别定义了 2 个、3 个子问题，但是子问题的拆分方式和计算顺序都是非常相似的。把两道题目放在一起对比的话，可以很快理解动态规划定义多个子问题的套路。
著名的股票买卖问题也是一个常见的定义多个子问题的题目。不过由于股票买卖问题中有一个重要的定义「状态机」的步骤，不太适合作为本期的例题。
在下一篇文章中，我会详细讲解股票买卖问题的解题思路，主要是如何在定义多个子问题的基础上加上状态机的推导。敬请期待。
往期文章
LeetCode 例题精讲 | 16 最大子数组和：子数组类问题的动态规划技巧
经典动态规划：编辑距离
动态规划只能用来求最值吗？
我是 nettee，致力于分享面试算法的解题套路，让你真正掌握解题技巧，做到举一反三。我的《LeetCode 例题精讲》系列文章正在写作中，关注我的公众号，获取最新文章。
