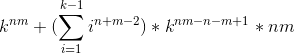The 2016 ACM-ICPC Asia China-Final (Shanghai) Contest---重现赛题解
A - Number Theory Problem(规律)
题意:
Mr. Panda is one of the top specialists on number theory all over the world. Now Mr. Panda is investigating the property of the powers of 2. Since 7 is the lucky number of Mr. Panda, he is always interested in the number that is a multiple of 7. However, we know that there is no power of 2 that is a multiple of 7, but a power of 2 subtracted by one can be a multiple of 7. Mr. Panda wants to know how many positive integers less than 2 N in the form of 2 k − 1 (k is a positive integer) that is divisible by 7. N is a positive interger given by Mr Panda.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case contains only one positive interger N.
Output
For each test case, output one line containing ‘Case #x: y’, where x is the test case number (starting from 1) and y is the answer. Limits: • 1 ≤ T ≤ 100. • 1 ≤ N ≤ 105 .
思路:一开始用java的大数直接预处理算的,结果T了,,,可能是大数太大造成超时,后来队友发现规律,,,每3
个+1,,用C++也一样。。
代码:
import java.math.BigInteger;
import java.util.*;
public class Main
{
public static void main(String args[])
{
Scanner cin = new Scanner(System.in);
int n,T,cas=0;
int num[]=new int[100005];
num[1]=num[2]=num[0]=0;
int res=1;
for(int i=3;i<=100000;i+=3)
{
num[i+0]=res;
num[i+1]=res;
num[i+2]=res;
res++;
}
T=cin.nextInt();
while(T-->0)
{
n=cin.nextInt();
System.out.println("Case #"+(++cas)+": " + num[n]);
}
cin.close();
}
}L - World Cup(二分+贪心//数据太水)
题意:
Here is World Cup again, the top 32 teams come together to fight for the World Champion. The teams are assigned into 8 groups, with 4 teams in each group. Every two teams in the same group will play a game (so there are totally 6 games in each group), and the winner of this game gets 3 points, loser gets 0 point. If it is a tie game, both teams get 1 point. After all games finished, we get the scoreboard, but we forget the result of each game, can you help us to figure the result of each game? We only care about the win/lose/tie result of each game, but we don’t care the goals in each game.
Input
The input starts with one line containing exactly one integer T, which is the number of test cases. Each test case contains four space-separated integers A, B, C, D, in a line, which indicate the points each team gets after all 6 games.
Output
For each test case, output one line containing ‘Case #x: y’, where x is the test case number (starting from 1) and y is ‘Yes’ if you can point out the result of each game, or ‘No’ if there are multiple game results satisfy the scoreboard, or ‘Wrong Scoreboard’ if there is no game result matches the scoreboard. Limits: • 1 ≤ T ≤ 100. • 0 ≤ A, B, C, D ≤ 100.
Notes:In sample case #1, the only scenaro will be: the first team wins all the three games it plays, the second team loses to the first team and wins the other two, the third team only wins the game with the fourth, and the fourth team lose all the games. In sample case #2, the fourth team loses all the games, and the first three teams get into a winningcycle, but there may be two different winning-cycles: first team wins second team, second team wins third team, third team wins first team OR first team wins third team, third team wins second team, second team wins first team. We can’t figure which winning-cycle is the actual game result. In sample case #3, the first team get 10 points, but no team could get more than 9 points by play three games, so it is a wrong scoreboard.
思路:dfs枚举出所有可能情况的结果,然后根据输入一一比对,然后判断输出就可以了
代码:
#include
using namespace std;
int cas,T,a[10],ans,pp[10000][10],ss,ok,t;
int x[10]={0,1,1,1,2,2,3},y[10]={0,2,3,4,3,4,4},sum[10];
int dfs(int c,int v)
{//cout< D - Ice Cream Tower
题意:
Mr. Panda likes ice cream very much especially the ice cream tower. An ice cream tower consists of K ice cream balls stacking up as a tower. In order to make the tower stable, the lower ice cream ball should be at least twice as large as the ball right above it. In other words, if the sizes of the ice cream balls from top to bottom are A0, A1, A2, · · · , AK−1, then A0 × 2 ≤ A1, A1 × 2 ≤ A2, etc. One day Mr. Panda was walking along the street and found a shop selling ice cream balls. There are N ice cream balls on sell and the sizes are B0, B1, B2, · · · , BN−1 . Mr. Panda was wondering the maximal number of ice cream towers could be made by these balls.
Input
The first line of the input gives the number of test cases, T. T test cases follow. Each test case starts with a line consisting of 2 integers, N the number of ice cream balls in shop and K the number of balls needed to form an ice cream tower. The next line consists of N integers representing the size of ice cream balls in shop.
Output
For each test case, output one line containing ‘Case #x: y’, where x is the test case number (starting from 1) and y is the maximal number of ice cream towers could be made. Limits: • 1 ≤ T ≤ 100. • 1 ≤ N ≤ 3 × 105 . • 1 ≤ K ≤ 64. • 1 ≤ Bi ≤ 1018 .
思路:二分答案,对于每个mid判是否能构成mid个k层的ice。判断方法是,在所有冰淇淋上一层一层的从小到大加。
先给每个冰淇淋的第一层依次都放上,然后在依次放合法的到第二层。。。直到第k层。
对于小的下面放大的球,若两个冰淇淋的第一层是a b。a 代码: Mr. Panda likes playing puzzles with grid paper. Recently he invented a new rule to play with the grid paper. At the beginning, he grabs a grid paper with N rows and M columns. Then he fills each cell an integer in the range of [1, K]. After filling all the cells, he starts finding Great cells in the grid. A cell is called Great cell if and only if it meets the following 2 conditions: • The value in the cell is strictly larger than other cells in the same row. • The value in the cell is strictly larger than other cells in the same column. Now Mr. Panda is wondering how many different ways he can fill the grid paper so that there are exactly g Great cells. As Mr. Panda likes simple conclusion number, let’s just tell him the value NM ∑ g=0 (g + 1) · Ag mod (109 + 7) Ag represents the number of different ways Mr. Panda can fill the grid paper such that there are exactly g Great cells. The first line of the input gives the number of test cases, T. T lines follow. Each line represents a test case containing 3 integers N, M representing the number of rows and columns of the grid paper, K representing the range for filling numbers. For each test case, first output one line containing ‘Case #x: y’, where x is the test case number (starting from 1), y is the simple conclusion number for Mr. Panda. Limits: • 1 ≤ T ≤ 20. • 1 ≤ N, M, K ≤ 200. Note: For the first sample, A0 = 10, A1 = 4, A2 = 2, A3 = A4 = 0, thus the answer is 10+4×2+2×3 = 24. 思路:换个思路,推公式。把括号拆出来, 每个位置是好数的次数都相等//*(nm),对于每个位置,是好数可以取的值(i+1)是在[2,k]范围,一行一列的其他位置是可以取[1,i],就是 代码: The Codejamon game is on fire! Fans across the world are predicting and betting on which team will win the game. A gambling company is providing betting odds for all teams; the odds for the i-th team is Ai : Bi . For each team, you can bet any positive amount of money, and you do not have to bet the same amount on each team. If the i-th team wins, you get your bet on that team back, plus Bi Ai times your bet on that team. For example, suppose that there are two teams, with odds of 5:3 and 2:7 and you bet $20 on the first team and $10 on the second team. If the first team wins, you will lose your $10 bet on the second team, but you will receive your $20 bet back, plus 3 5 × 20 = 12, so you will have a total of $32 at the end. If the second team wins, you will lose your $20 bet on the first team, but you will receive your $10 bet back, plus 7 2 × 10 = 35, so you will have a total of $45 at the end. Either way, you will have more money than you bet ($20+$10=$30). As a greedy fan, you want to bet on as many teams as possible to make sure that as long as one of them wins, you will always end up with more money than you bet. Can you figure out how many teams you can bet on? The input starts with one line containing exactly one integer T, which is the number of test cases. Each test case starts with one line containing an integer N: the number of teams in the game. Then, N more lines follow. Each line is a pair of numbers in the form ‘Ai:Bi ’ (that is, a number Ai , followed by a colon, then a number Bi , with no spaces in between), indicating the odds for the i-th team. For each test case, output one line containing ‘Case #x: y’, where x is the test case number (starting from 1) and y is the maximum number of teams that you can bet on, under the conditions specified in the problem statement. Limits: • 1 ≤ T ≤ 100. • 1 ≤ N ≤ 100. • 0 < Ai , Bi < 100. • Both Ai and Bi have at most 3 digits after the decimal point. Note: In sample case #1, one optimal strategy is to bet 1.5 dollars on the first team and 1.5 dollars on the third team. If the first team wins, you will get 1.5 + 1.5 × (1.1/1) = 3.15 dollars back, and if the third team wins, you will get 1.5 + (1.7/1.5) × 1.5 = 3.2 dollars back. Both of these are higher than the total money that you bet (1.5 + 1.5 = 3 dollars). However, there is no way to bet on all three teams and be guaranteed a profit. 思路:简单转化一下公式,据说是个高精度的题,但是long double也能过 代码: #include H - Great Cells
题意:
Input
Output
![]() 就是所有情况数
就是所有情况数 ![]() 。
。![]() 可以理解为,所有位置是好数的次数和,然后就推一下公式就可以了。
可以理解为,所有位置是好数的次数和,然后就推一下公式就可以了。![]() ,非同行同列的其他 nm-n-m+1给格子[1,k]随便取值.
,非同行同列的其他 nm-n-m+1给格子[1,k]随便取值.#include E - Bet(数学公式+高精度)
题意:
Input
Output
![]() 要数量最多,那么
要数量最多,那么![]() 要尽量小,所以就按
要尽量小,所以就按![]() 小的排序。一直加到>1就停下。
小的排序。一直加到>1就停下。#include