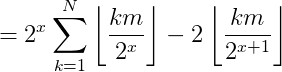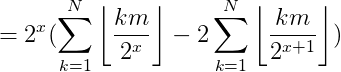- 备战CSP(1):复习图论之最短路算法SPFA
鹤上听雷
算法图论
接下来,我们将用这道题目来复习最短路算法,dijk和spfa。LuoguP3371【模板】单源最短路径(弱化版)题目背景本题测试数据为随机数据,在考试中可能会出现构造数据让SPFA不通过,如有需要请移步P4779。题目描述如题,给出一个有向图,请输出从某一点出发到所有点的最短路径长度。输入格式第一行包含三个整数n,m,sn,m,sn,m,s,分别表示点的个数、有向边的个数、出发点的编号。接下来mm
- buuctf [极客大挑战 2019]FinalSQL
cng_Capricornus
buuctfweb安全
进入题目,又是这个作者,试试万能密码经过实验,双写什么的都没用。作者说的神秘代码,点进去发现url变了发现并没有什么卵用……正当我没有头绪的时候,我突然看到一句话,审题真的很重要:盲注!这里附上大佬的脚本:importrequestsimporttimeurl="http://def9937b-1746-4f41-98c7-a2b55b95664a.node4.buuoj.cn:81/search
- 八月刷题总结
Uzero.
ctf
2021DASCTFJulyXCBCTF--catflag考察日志文件位置,escapeshellarg函数绕过DASCTFJulyXCBCTF4th--ezrceYAPIMock远程代码执行漏洞BUUCTF--[HarekazeCTF2019]EasyNotesSESSION反序列化BUUCTF--[SWPU2019]Web3伪造Session,生成linux中的软链接BUUCTF--[wate
- [BUUCTF][极客大挑战 2019]PHP
朋克归零膏
CTFphplinuxfirefox
备份根据提示应该就是网站备份文件能被爆破出来随手写了个爆破脚本,基于御剑字典,只供学习使用importrandomimportrequestsimporttimefrommultiprocessingimportPooldefmultiScan(target,file_name,pool_num,delay):local_pool=Pool(pool_num)dirs=get_path_dict(
- BUUCTF [极客大挑战 2019]Secret File 1
THEMIScale
还差一步这道题就出来了在想了在想了别骂了别骂了打开题目后一片黑这个时候根据经验有事没事先ctrl+a安排一下果然有问题在最下方有一个连接打开链接出现一个按钮按他就完事了并没有出来什么用burp拦截后发现提示:secr3t.php打开后提示flag在flag.php中并且给了一串php其中stristr函数不用绕过直接干就完了然后就是啊哈!你找到我了!可是你看不到我QAQ~~~我就在这里这边最后请教
- macos的图标过大,这是因为有自己的设计规范
1024小神
苹果开发设计规范
苹果官方链接:App图标|AppleDeveloperDocumentation这个在官方文档里有说明,并且提供了sketch和ps的模板。figma还提供了模板:Figma
- 前端——vue代码结构
Alisazxy
前端
默认代码结构README.md---项目说明文件package.json---定义了这个项目所需要的各种模块,以及项目的配置信息(比如名称、版本、许可证等元数据)。package-lock.json---会自动为npm修改node_modules树或任何操作而生成package.jsonLICENSE---开源协议index.html---项目默认首页模板.postcssrc.js---是对pos
- BUUCTF:[ISITDTU 2019]EasyPHP --- rce 超级异或,,,吐了,,,字符之间异或, 成型的异或payload!!!
Zero_Adam
BUUCTF刷题记录RCEpython
目录:一、自己做:二、学的的三、学习WP1.这里先来个不限制字符个数的关于这个%ff以及异或的事情,咱们好好唠唠1.生成异或中间值的python脚本2.看有字符限制的时候,:参考:末初一、自己做:0xd)die('youaresoclose,omg');eval($_);?>过滤了,不少,我一般碰到rce的题,就看自己的笔记,然后把payload一股脑的网上怼,,,二、学的的正则看不明白的时候,可
- 模板-富文本
晓风残月Yuperman
nginx运维
博主介绍:大家好,我是想成为Super的Yuperman,互联网宇宙厂经验,17年医疗健康行业的码拉松奔跑者,曾担任技术专家、架构师、研发总监负责和主导多个应用架构。近期专注:RPA应用研究,主流厂商产品使用,开源RPA应用,包括UI.Vision、taskUI、taskt、OpenRpa、RobotFramework等技术范围:长期专注java体系,软件架构,DDD,多年java、golang、
- python exe site-package
weixin_33735077
python
2019独角兽企业重金招聘Python工程师标准>>>pythonexesite-package:http://www.lfd.uci.edu/~gohlke/pythonlibs/#pillow转载于:https://my.oschina.net/zuoan001/blog/346126
- 代码随想录算法训练营Day38||完全背包问题、leetcode 518. 零钱兑换 II 、 377. 组合总和 Ⅳ 、70. 爬楼梯 (进阶)
jiegongzhu3z
算法leetcode职场和发展
一、完全背包问题相较于01背包,完全背包的显著特征是每个物品可以用无数次,遍历顺序也不需要为了保证每个物品只去一次而倒序遍历。#include#includeusingnamespacestd;intmain(){intN,V;cin>>N>>V;vectorweight(N+1,0);vectorvalue(N+1,0);for(inti=0;i>weight[i]>>value[i];}vec
- 探索高效图像识别:基于OpenCV的形状匹配利器
崔庭盼Melvina
探索高效图像识别:基于OpenCV的形状匹配利器【下载地址】形状匹配find_scaled_shape_model资源文件本资源文件提供了使用OpenCV实现Halcon中算子`find_scaled_shape_model`的功能。该功能主要用于在图像中查找与模板形状相似的目标,并支持缩放变换。具体实现细节和使用方法可以参考相关博客文章项目地址:https://gitcode.com/open-
- cpu 调频策略
weixin_33814685
python
2019独角兽企业重金招聘Python工程师标准>>>调频策略通常有如下:1.Performance:CPUfreq被设置成scaling_min_freq和scaling_max_freq中的最高频率,2.Powersave::CPUfreq被设置成scaling_min_freq和scaling_max_freq中的最低频率;3.Userspace:允许root权限的用户通过sysfs的“sc
- 离散化、贪心、双指针、二分、倍增、构造、位运算
那只狸花猫吖
蓝桥杯算法
目录八、离散化1、离散化简介九、贪心1、贪心的概念十、双指针1、双指针简介2、对撞指针3、快慢指针十一、二分1、二分的概念2、二分的两种模板十二、倍增1、定义十三、构造1、定义十四、位运算1、位运算概述八、离散化1、离散化简介把无限空间中有限的个体映射到有限的空间中去,以此提高算法的时空效率。离散化是一种将数组的值域压缩,从而更加关注元素的大小关系的算法。当原数组中的数字很大、负数、小数时(大多数
- python建模的步骤_python基础教程之Python 建模步骤|python基础教程|python入门|python教程...
谭俊云
python建模的步骤
#%%#载入数据、查看相关信息importpandasaspdimportnumpyasnpfromsklearn.preprocessingimportLabelEncoderprint('第一步:加载、查看数据')file_path=r'D:\train\201905data\liwang.csv'band_data=pd.read_csv(file_path,encoding='UTF-8'
- 蓝桥杯备考:前缀和算法---模板题
无敌大饺子 1
蓝桥杯职场和发展
【模板】前缀和这道题,如果我们简单的用暴力解法,时间复杂度就是O(q*N)也就是10的十次方,这时候我们就会超时我们要学习一种前缀和的算法,它能帮助我们做一些预处理,用空间复杂度代替时间复杂度,比如说这道题,我们开辟一个数组,f[N],我们只需要一个公式f[i]=f[i-1]+a[i]就能完成我们的预处理,最后查询的时间复杂度就是O(1)了,比如我们要查询l到r的和,我们就让f[r]-f[l-1]
- Pycharm、IDEA等汉化教程
neo_will_mvp
Python和GO实操生产代码Pycharm汉化Pycharm汉化
本汉化教程对jetbrains全系列可用:IDEA、Pycharm、WebStorm、phpstorm、AndroidStudio、GoLand、RubyMine、CLion此汉化无副作用,绝对安全2019.02.03今天对汉化教程进行改版,解决原教程的汉化会导致setting无法使用和Structure无法显示问题此教程中使用的汉化包并非本人所产,我只是个搬运工。作者为:平方X,感兴趣的同学可以
- 【代码随想录训练营】【Day01】第一章|数组|数组理论基础|704.二分查找|27.移除元素
蚝油菜花
算法leetcode代码随想录
数组理论基础数组是在编程中非常常见的数据存储结构,主要有以下几个特点:数组的存储地址是一片连续的空间数组中存储的元素都是相同类型的修改数组中某一元素的值时,只能覆盖(重新赋值)更多有关数组的理论基础可查阅:《代码随想录》数组理论基础704.二分查找题目详细:LeetCode.704注意:二分查找对数据样本有明确的要求,即数组中的元素是有序的,所以在今后遇到类似于“在有序的数据样本中查找某一目标数据
- 【代码随想录训练营】【Day03】第二章|链表|链表理论基础|203.移除链表元素|707.设计链表|206.反转链表
蚝油菜花
链表数据结构
链表理论基础链表的结构类似于一串珠子,每一颗珠子就相当于链表上的一个节点;每一个节点则由数据域和指针域构成,数据域用于存放数据,指针域用于指向其它一个节点或空节点(链表尾部)。链表与数组的主要区别在于:数组是在内存中是连续分布的,但是链表在内存中不是连续分布的。数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。链表的长度是不固定的,可以进行动态增删,适合数据量不固
- 代码随想录训练营Day3|Leetcode 203.移除链表元素 Leetcode 707.设计链表 Leetcode 206.反转链表
?��??
leetcode链表算法
编程语言:C#链表定义*publicclassListNode{*publicintval;*publicListNodenext;*publicListNode(intval=0,ListNodenext=null){*this.val=val;*this.next=next;*}*}Leetcode203.移除链表元素题目链接:203.移除链表元素-力扣(LeetCode)题意:删除链表中等于
- 基于Spring Boot的校园志愿者服务网站
超级无敌暴龙战士塔塔开
Java课设与毕设资源springbootjava后端
文章目录项目介绍主要功能截图:登录个人中心志愿者管理活动类型管理活动报名管理活动心得部分代码展示设计总结项目获取方式作者主页:Java韩立简介:Java领域优质创作者、简历模板、学习资料、面试题库【关注我,都给你】文末获取源码联系项目介绍校园志愿者服务网站,java项目,springboot项目。eclipse和idea都能打开运行。推荐环境配置:eclipse/ideajdk1.8mavenmy
- 【C语言】带头双向循环链表(list)详解(定义、增、删、查、改)
Morning_Yang丶
数据结构链表c语言list
博客主页:要早起的杨同学的博客欢迎关注点赞收藏⭐️留言本文所属专栏:【数据结构】✉️坚持和努力从早起开始!参考在线编程网站:牛客网力扣作者水平有限,如果发现错误,敬请指正!感谢感谢!前言实际中链表的结构非常多样,上篇单链表博文中我们介绍了8种链表结构,但实际中最常用的还是这两种结构无头单向非循环链表:结构简单,一般不会单独用来存数据。实际中更多是作为其他数据结构的子结构,如哈希桶、图的邻接表等等。
- python cv2 matchtemplate_机器学习进阶-图像金字塔与轮廓检测-模板匹配(单目标匹配和多目标匹配)1.cv2.matchTemplate(进行模板匹配) 2.cv2.minMa...
weixin_39621044
pythoncv2matchtemplate
1.cv2.matchTemplate(src,template,method)#用于进行模板匹配参数说明:src目标图像,template模板,method使用什么指标做模板的匹配度指标2.min_val,max_val,min_loc,max_loc=cv2.minMaxLoc(ret)#找出矩阵中最大值和最小值,即其对应的(x,y)的位置参数说明:min_val,max_val,min_lo
- 根据每月流量和市场份额排名前20 的AI工具列表
开心的AI频道
人工智能
ChatGPT:由OpenAI研发,是一款对话式大型语言模型。它能够理解自然语言输入,生成连贯且符合逻辑的回复。可用于文本创作,如撰写文章、故事、诗歌;还能解答各种领域的知识问题,提供翻译、代码解释等服务,在多种场景下辅助用户解决语言相关需求。Canva:作为在线图形设计平台,拥有海量的模板资源,涵盖海报、名片、社交媒体帖子、演示文稿等多种类型。用户无需专业设计技能,通过简单的拖放操作即可使用其丰
- 创建Unity项目、Android打包和打包踩坑
NuageL
虚拟恋人unity游戏引擎
1.安装Unity和配置开发环境2.创建3D项目打开UnityHub,点击“Projects”选项卡。点击右上角的“NewProject”,选择“3D”模板,给项目命名,并选择存储位置。点击“Create”开始创建项目。3.配置Android构建设置打开Unity项目后,点击菜单栏的File>BuildProfile(版本6000.0.25f1c1,其他版本在File>BuildSettings中
- 软件测试-等价类划分法测试用例设计二
minaMoonGirl
测试用例
一、设某公司要打印2015~2019年的报表,其中报表日期为6位数字组成,其中,前4位为年份,后两位为月份。针对上述需求分析,先编写一个对报表日期合法性检查的C程序,然后按照等价类划分法设计测试用例(弱健壮覆盖标准),最后运行设计的测试用例。等价类划分模板如下:条件有效等价类编号无效等价类编号测试用例模板如下:用例编号测试数据期望结果覆盖等价类解答:等价类划分:条件有效等价类编号年份月份皆符合01
- 洛谷P3372 【模板】线段树 1
xwztdas
数据结构
洛谷题目传送门题目描述如题,已知一个数列,你需要进行下面两种操作:将某区间每一个数加上k。求出某区间每一个数的和。输入格式第一行包含两个整数,,分别表示该数列数字的个数和操作的总个数。第二行包含个用空格分隔的整数,其中第个数字表示数列第项的初始值。接下来行每行包含3或4个整数,表示一个操作,具体如下:1xyk:将区间[,]内每个数加上k。2xy:输出区间[,]内每个数的和。输出格式输出包含若干行整
- 探索未来开发的新起点:NetCore-Boilerplate
侯深业Dorian
探索未来开发的新起点:NetCore-Boilerplatenetcore-boilerplateBoilerplateofAPIin.NET7项目地址:https://gitcode.com/gh_mirrors/ne/netcore-boilerplate是一个强大的、基于.NETCore的现代Web应用模板,它提供了全面的基础架构和最佳实践,为开发者快速启动新的Web项目提供了便利。该项目旨
- echarts样式设置笔记
weixin_45907672
vueecharts前端javascript
设置x轴的小标题xAxis:{type:'value',name:'DRGs组数',data:['2014','2015','2016','2017','2018','2019','2020']}设置y轴的小标题yAxis:[{type:'value',name:'预算总额',min:0,max:25,interval:5,//可以添加单位和后缀//axisLabel:{//formatter:'
- 光通信网络设备急速发展,光网络架构剧烈变革
SugarNMS
行业网管网管平台网管软件光设备光网络设备管理网管开发
数据表明,IP数据流量从2010年到2014年期间翻了5倍,未来仍将保持23%的复合增长率,而移动流量在2014年增长了69%,到2019年将为2014年的10倍,急剧增长的数据流量对底层光网络设备带宽和容量提出了更高要求。同时,随着全球信息化发展和ICT融合加剧,IT理念渗透到传统通信的各个领域,光网络架构面临变革,将深刻影响光网络设备的发展。光通信网络设备业务发展正驱动着光网络架构的变革,以适
- ztree异步加载
3213213333332132
JavaScriptAjaxjsonWebztree
相信新手用ztree的时候,对异步加载会有些困惑,我开始的时候也是看了API花了些时间才搞定了异步加载,在这里分享给大家。
我后台代码生成的是json格式的数据,数据大家按各自的需求生成,这里只给出前端的代码。
设置setting,这里只关注async属性的配置
var setting = {
//异步加载配置
- thirft rpc 具体调用流程
BlueSkator
中间件rpcthrift
Thrift调用过程中,Thrift客户端和服务器之间主要用到传输层类、协议层类和处理类三个主要的核心类,这三个类的相互协作共同完成rpc的整个调用过程。在调用过程中将按照以下顺序进行协同工作:
(1) 将客户端程序调用的函数名和参数传递给协议层(TProtocol),协议
- 异或运算推导, 交换数据
dcj3sjt126com
PHP异或^
/*
* 5 0101
* 9 1010
*
* 5 ^ 5
* 0101
* 0101
* -----
* 0000
* 得出第一个规律: 相同的数进行异或, 结果是0
*
* 9 ^ 5 ^ 6
* 1010
* 0101
* ----
* 1111
*
* 1111
* 0110
* ----
* 1001
- 事件源对象
周华华
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- MySql配置及相关命令
g21121
mysql
MySQL安装完毕后我们需要对它进行一些设置及性能优化,主要包括字符集设置,启动设置,连接优化,表优化,分区优化等等。
一 修改MySQL密码及用户
- [简单]poi删除excel 2007超链接
53873039oycg
Excel
采用解析sheet.xml方式删除超链接,缺点是要打开文件2次,代码如下:
public void removeExcel2007AllHyperLink(String filePath) throws Exception {
OPCPackage ocPkg = OPCPac
- Struts2添加 open flash chart
云端月影
准备以下开源项目:
1. Struts 2.1.6
2. Open Flash Chart 2 Version 2 Lug Wyrm Charmer (28th, July 2009)
3. jofc2,这东西不知道是没做好还是什么意思,好像和ofc2不怎么匹配,最好下源码,有什么问题直接改。
4. log4j
用eclipse新建动态网站,取名OFC2Demo,将Struts2 l
- spring包详解
aijuans
spring
下载的spring包中文件及各种包众多,在项目中往往只有部分是我们必须的,如果不清楚什么时候需要什么包的话,看看下面就知道了。 aspectj目录下是在Spring框架下使用aspectj的源代码和测试程序文件。Aspectj是java最早的提供AOP的应用框架。 dist 目录下是Spring 的发布包,关于发布包下面会详细进行说明。 docs&nb
- 网站推广之seo概念
antonyup_2006
算法Web应用服务器搜索引擎Google
持续开发一年多的b2c网站终于在08年10月23日上线了。作为开发人员的我在修改bug的同时,准备了解下网站的推广分析策略。
所谓网站推广,目的在于让尽可能多的潜在用户了解并访问网站,通过网站获得有关产品和服务等信息,为最终形成购买决策提供支持。
网站推广策略有很多,seo,email,adv
- 单例模式,sql注入,序列
百合不是茶
单例模式序列sql注入预编译
序列在前面写过有关的博客,也有过总结,但是今天在做一个JDBC操作数据库的相关内容时 需要使用序列创建一个自增长的字段 居然不会了,所以将序列写在本篇的前面
1,序列是一个保存数据连续的增长的一种方式;
序列的创建;
CREATE SEQUENCE seq_pro
2 INCREMENT BY 1 -- 每次加几个
3
- Mockito单元测试实例
bijian1013
单元测试mockito
Mockito单元测试实例:
public class SettingServiceTest {
private List<PersonDTO> personList = new ArrayList<PersonDTO>();
@InjectMocks
private SettingPojoService settin
- 精通Oracle10编程SQL(9)使用游标
bijian1013
oracle数据库plsql
/*
*使用游标
*/
--显示游标
--在显式游标中使用FETCH...INTO语句
DECLARE
CURSOR emp_cursor is
select ename,sal from emp where deptno=1;
v_ename emp.ename%TYPE;
v_sal emp.sal%TYPE;
begin
ope
- 【Java语言】动态代理
bit1129
java语言
JDK接口动态代理
JDK自带的动态代理通过动态的根据接口生成字节码(实现接口的一个具体类)的方式,为接口的实现类提供代理。被代理的对象和代理对象通过InvocationHandler建立关联
package com.tom;
import com.tom.model.User;
import com.tom.service.IUserService;
- Java通信之URL通信基础
白糖_
javajdkwebservice网络协议ITeye
java对网络通信以及提供了比较全面的jdk支持,java.net包能让程序员直接在程序中实现网络通信。
在技术日新月异的现在,我们能通过很多方式实现数据通信,比如webservice、url通信、socket通信等等,今天简单介绍下URL通信。
学习准备:建议首先学习java的IO基础知识
URL是统一资源定位器的简写,URL可以访问Internet和www,可以通过url
- 博弈Java讲义 - Java线程同步 (1)
boyitech
java多线程同步锁
在并发编程中经常会碰到多个执行线程共享资源的问题。例如多个线程同时读写文件,共用数据库连接,全局的计数器等。如果不处理好多线程之间的同步问题很容易引起状态不一致或者其他的错误。
同步不仅可以阻止一个线程看到对象处于不一致的状态,它还可以保证进入同步方法或者块的每个线程,都看到由同一锁保护的之前所有的修改结果。处理同步的关键就是要正确的识别临界条件(cri
- java-给定字符串,删除开始和结尾处的空格,并将中间的多个连续的空格合并成一个。
bylijinnan
java
public class DeleteExtraSpace {
/**
* 题目:给定字符串,删除开始和结尾处的空格,并将中间的多个连续的空格合并成一个。
* 方法1.用已有的String类的trim和replaceAll方法
* 方法2.全部用正则表达式,这个我不熟
* 方法3.“重新发明轮子”,从头遍历一次
*/
public static v
- An error has occurred.See the log file错误解决!
Kai_Ge
MyEclipse
今天早上打开MyEclipse时,自动关闭!弹出An error has occurred.See the log file错误提示!
很郁闷昨天启动和关闭还好着!!!打开几次依然报此错误,确定不是眼花了!
打开日志文件!找到当日错误文件内容:
--------------------------------------------------------------------------
- [矿业与工业]修建一个空间矿床开采站要多少钱?
comsci
地球上的钛金属矿藏已经接近枯竭...........
我们在冥王星的一颗卫星上面发现一些具有开采价值的矿床.....
那么,现在要编制一个预算,提交给财政部门..
- 解析Google Map Routes
dai_lm
google api
为了获得从A点到B点的路劲,经常会使用Google提供的API,例如
[url]
http://maps.googleapis.com/maps/api/directions/json?origin=40.7144,-74.0060&destination=47.6063,-122.3204&sensor=false
[/url]
从返回的结果上,大致可以了解应该怎么走,但
- SQL还有多少“理所应当”?
datamachine
sql
转贴存档,原帖地址:http://blog.chinaunix.net/uid-29242841-id-3968998.html、http://blog.chinaunix.net/uid-29242841-id-3971046.html!
------------------------------------华丽的分割线--------------------------------
- Yii使用Ajax验证时,如何设置某些字段不需要验证
dcj3sjt126com
Ajaxyii
经常像你注册页面,你可能非常希望只需要Ajax去验证用户名和Email,而不需要使用Ajax再去验证密码,默认如果你使用Yii 内置的ajax验证Form,例如:
$form=$this->beginWidget('CActiveForm', array( 'id'=>'usuario-form',&
- 使用git同步网站代码
dcj3sjt126com
crontabgit
转自:http://ued.ctrip.com/blog/?p=3646?tn=gongxinjun.com
管理一网站,最开始使用的虚拟空间,采用提供商支持的ftp上传网站文件,后换用vps,vps可以自己搭建ftp的,但是懒得搞,直接使用scp传输文件到服务器,现在需要更新文件到服务器,使用scp真的很烦。发现本人就职的公司,采用的git+rsync的方式来管理、同步代码,遂
- sql基本操作
蕃薯耀
sqlsql基本操作sql常用操作
sql基本操作
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
蕃薯耀 2015年6月1日 17:30:33 星期一
&
- Spring4+Hibernate4+Atomikos3.3多数据源事务管理
hanqunfeng
Hibernate4
Spring3+后不再对JTOM提供支持,所以可以改用Atomikos管理多数据源事务。Spring2.5+Hibernate3+JTOM参考:http://hanqunfeng.iteye.com/blog/1554251Atomikos官网网站:http://www.atomikos.com/ 一.pom.xml
<dependency>
<
- jquery中两个值得注意的方法one()和trigger()方法
jackyrong
trigger
在jquery中,有两个值得注意但容易忽视的方法,分别是one()方法和trigger()方法,这是从国内作者<<jquery权威指南》一书中看到不错的介绍
1) one方法
one方法的功能是让所选定的元素绑定一个仅触发一次的处理函数,格式为
one(type,${data},fn)
&nb
- 拿工资不仅仅是让你写代码的
lampcy
工作面试咨询
这是我对团队每个新进员工说的第一件事情。这句话的意思是,我并不关心你是如何快速完成任务的,哪怕代码很差,只要它像救生艇通气门一样管用就行。这句话也是我最喜欢的座右铭之一。
这个说法其实很合理:我们的工作是思考客户提出的问题,然后制定解决方案。思考第一,代码第二,公司请我们的最终目的不是写代码,而是想出解决方案。
话粗理不粗。
付你薪水不是让你来思考的,也不是让你来写代码的,你的目的是交付产品
- 架构师之对象操作----------对象的效率复制和判断是否全为空
nannan408
架构师
1.前言。
如题。
2.代码。
(1)对象的复制,比spring的beanCopier在大并发下效率要高,利用net.sf.cglib.beans.BeanCopier
Src src=new Src();
BeanCopier beanCopier = BeanCopier.create(Src.class, Des.class, false);
- ajax 被缓存的解决方案
Rainbow702
JavaScriptjqueryAjaxcache缓存
使用jquery的ajax来发送请求进行局部刷新画面,各位可能都做过。
今天碰到一个奇怪的现象,就是,同一个ajax请求,在chrome中,不论发送多少次,都可以发送至服务器端,而不会被缓存。但是,换成在IE下的时候,发现,同一个ajax请求,会发生被缓存的情况,只有第一次才会被发送至服务器端,之后的不会再被发送。郁闷。
解决方法如下:
① 直接使用 JQuery提供的 “cache”参数,
- 修改date.toLocaleString()的警告
tntxia
String
我们在写程序的时候,经常要查看时间,所以我们经常会用到date.toLocaleString(),但是date.toLocaleString()是一个过时 的API,代替的方法如下:
package com.tntxia.htmlmaker.util;
import java.text.SimpleDateFormat;
import java.util.
- 项目完成后的小总结
xiaomiya
js总结项目
项目完成了,突然想做个总结但是有点无从下手了。
做之前对于客户端给的接口很模式。然而定义好了格式要求就如此的愉快了。
先说说项目主要实现的功能吧
1,按键精灵
2,获取行情数据
3,各种input输入条件判断
4,发送数据(有json格式和string格式)
5,获取预警条件列表和预警结果列表,
6,排序,
7,预警结果分页获取
8,导出文件(excel,text等)
9,修