牛客挑战赛39(A(枚举+递增+二分),B(二分+hash),C(线段树-等差数组),E(杨辉三角组合数))
题目链接
A-聚会
题意:
做法:看了别人的代码我觉得我的做法太复杂了。
稍微分析下一个可做的做法:两个传送,一定一个在0处,否则相当于没用
正数负数分开考虑,对于正数数组,排序后 一定是某个i与最后一个的中间位置放置一个传送,那我们就枚举中间的位置,然后计算当前最大距离。
且一定是这个传送门的左边的某些点 能往右走最近,那我用递增的方法,找到小于传送当前坐标t的第一个数:now,接着从now通过二分 找到最远 且往右边走小于左边走第一个点 这样就找到我想要的点了,维护一下即可
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=1e5+10;
ll n,a[N],x[N],y[N],l1,l2;
ll f[40],ans;
void run(ll x[],ll y[],ll len1,ll len2)
{
rep(i,1,len1)
{
ll t=(x[i]+x[len1])/2;
ll mx=max(y[len2],x[len1]-t);
int now=1;
for(int k=27;k>=0;--k){
if(now+f[k]>len1) continue;
if(x[now+f[k]]>=t) continue;
now=now+f[k];
}
int l=1,r=now;
while(l<=r)
{
int mid=l+r>>1;
if(x[mid]>t-x[mid]) r=mid-1,now=mid;
else l=mid+1;
}
mx=max(mx,min(x[now],t-x[now]));
if(now-1>0) mx=max(mx,min(x[now-1],t-x[now-1]));
//printf("now:%d mx:%lld t:%lld\n",now,mx,t);
ans=min(ans,mx);
}
}
void solve()
{
cin>>n;
ans=l1=l2=0;
rep(i,1,n)
{
scanf("%lld",&a[i]);ans=max(ans,abs(a[i]));
if(a[i]<0) x[++l1]=-a[i];else if(a[i]>0) y[++l2]=a[i];
}
sort(x+1,x+1+l1);
sort(y+1,y+1+l2);
run(x,y,l1,l2);
run(y,x,l2,l1);
printf("%lld\n",ans);
}
int main()
{
f[0]=1;
for(int i=1;i<=28;++i) f[i]=f[i-1]*2;
int _;cin>>_;while(_--)
solve();
}
/*
10
2
4 6
3
2 6 8
3
6 10 12
5
-5 -3 2 5 7
1
2
3
3
1 6 9
*/
B-密码系统
做法:枚举每轮k 以及各个下标(j+=k的枚举)
然后通过二分 判断当前位置j 和当前最小位置i 找到相同的前缀len 通过判断j+len 与i+len 的字符 来维护答案。
官方做法好像是后缀数组,不太会。。
#include
using namespace std;
const int N = 1e6 + 10;
//base[i]进制
typedef long long ll;
ll h[3][N];
ll base[3]={43,47,41};
ll mod[3] = {1000000007,998244353,1000000009};
ll f[3][N];
int n,k,ans[N];
int getid(char c) {
return c-'a';
}
char s[N];
void init()
{
f[1][0]=f[0][0]=1;
for(int i=1;i>1;
ll t1, t2;
t1=getvalue(x,x+mid-1,0);
t2=getvalue(y,y+mid-1,0);
//for(int j=0;j<=1;++j)
if(t1==t2) l=mid+1,ans=mid;
else r=mid-1;
}
return ans;
}
int main()
{
init();
cin>>n>>k;
cin>>s+1;
for(int i=1;i<=n;++i) s[n+i]=s[i];
n=2*n;
for(int i=1;i<=n;++i){
for(int j=0;j<=1;++j) h[j][i]=(h[j][i-1]*base[j]%mod[j]+getid(s[i]))%mod[j];
}
//puts("***");
for(int i=1;i<=k;++i){
ans[i]=i;
for(int j=i+k;j<=n;j+=k){
int len=get(ans[i],j);
//printf("i:%d j:%d len:%d\n",i,j,len);
if(len==k) continue;
if(s[ans[i]+len]s[ans[i]+len]) id=ans[i];
}
for(int i=0;i C-牛牛的等差数列
线段树 的模板题了
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=2e5+10;
const ll mod=111546435;
ll sum[4*N],lazy[4*N],D[4*N],pre[N];
int mp[50];
ll input(){
ll x=0,f=0;char ch=getchar();
while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return f? -x:x;
}
ll a[N];
int n;
void add(ll &x,ll y)
{
x=(x+y)%mod;
}
ll gets(ll a1,ll n,ll d)
{
return (n*a1%mod+n*(n-1)/2%mod*d%mod)%mod;
}
ll getv(ll a1,ll n,ll d)
{
return (a1+n*d%mod)%mod;
}
void pushdown(int id,int l,int r)
{
if(lazy[id]){
int mid=l+r>>1;
ll len1=mid-l+1,len2=r-mid;
add(lazy[id<<1],lazy[id]);
add(D[id<<1],D[id]);
ll newval=lazy[id]+len1*D[id]%mod;
newval%=mod;
add(lazy[id<<1|1],newval);
add(D[id<<1|1],D[id]);
add(sum[id<<1],gets(lazy[id],len1,D[id]));
add(sum[id<<1|1],gets(newval,len2,D[id]));
lazy[id]=D[id]=0;
}
}
void up(int id,int l,int r,int ql,int qr,ll val,ll d)
{
if(ql<=l&&r<=qr){
ll t=getv(val,l,d);
add(lazy[id],t);
add(D[id],d);
add(sum[id],gets(t,r-l+1,d));
return ;
}
pushdown(id,l,r);
int mid=l+r>>1;
if(ql<=mid) up(id<<1,l,mid,ql,qr,val,d);
if(qr>mid) up(id<<1|1,mid+1,r,ql,qr,val,d);
sum[id]=(sum[id<<1]+sum[id<<1|1])%mod;
}
ll qu(int id,int l,int r,int ql,int qr)
{
if(ql<=l&&r<=qr) return sum[id];
pushdown(id,l,r);int mid=l+r>>1;
ll res=0;
if(ql<=mid) res=qu(id<<1,l,mid,ql,qr);
if(qr>mid) add(res,qu(id<<1|1,mid+1,r,ql,qr));
return res;
}
int main()
{
pre[0]=0;
n=input();rep(i,1,n) {a[i]=input();pre[i]=(pre[i-1]+a[i])%mod;}
int q;q=input();while(q--){
int op;op=input();
ll l,r,val,d;
l=input();r=input();val=input();
if(l>r) swap(l,r);
if(op==1){
d=input();up(1,1,n,l,r,(val-l*d%mod+mod)%mod,d);
}
else {
ll ans=(qu(1,1,n,l,r)+pre[r]-pre[l-1]+mod)%mod;
printf("%lld\n",ans%val);
}
}
}
E-牛牛与序列
官方题解:
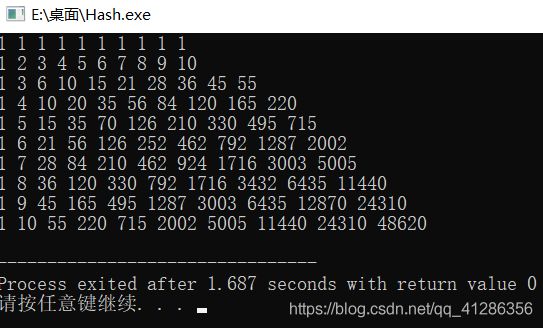
打表程序:
#includeusing namespace std; const int N=1e3+10; typedef long long ll; ll dp[N][N]; int n,k; int main() { n=10,k=10; for(int i=1;i<=k;++i) dp[1][i]=1; for(int i=2;i<=n;++i){ for(int now=1;now<=k;++now) for(int j=1;j<=now;++j){ dp[i][now]+=dp[i-1][j]; } } for(int i=1;i<=n;++i){ for(int j=1;j<=n;++j){ printf("%lld ",dp[i][j]); } puts(""); } }
打表结果:
典型的杨辉三角了。。
至于求组合数不能用lucas(我超时)原因是lucas的复杂度是log(n)*p p是模数,这里模数比较大,k比较小,考虑约分一下即可
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const ll p=998244353;
const ll mod=998244353;
const int N=1e6+10;
ll fac[N],inv[N],ifac[N];
ll C(int n,int m)
{
ll ans=1;
rep(i,1,m) ans=ans*(n-i+1)%mod;
return ans*ifac[m]%mod;
}
ll powmod(ll a,ll b,ll mod)
{
ll res=1;
for(;b;b>>=1){
if(b&1) res=res*a%mod;
a=a*a%mod;
}
return res;
}
void init()
{
fac[0]=inv[1]=ifac[0]=1;
rep(i,1,N-1) fac[i]=fac[i-1]*i%mod;
rep(i,2,N-1) inv[i]=inv[mod%i]*(mod-mod/i)%mod;
rep(i,1,N-1) ifac[i]=ifac[i-1]*inv[i]%mod;
}
int main()
{
init();
int _;cin>>_;while(_--)
{
ll n,k;
scanf("%lld%lld",&n,&k);
ll mi=min(k-1,n);
ll ans=((powmod(k,n,p)-2ll*C(n+k-1,mi)+p+p)%p+k)%p;
printf("%lld\n",ans);
}
}