DFS深度优先遍历理解

---

一、DFS

1.DFS原理

（1）DFS（Depth First Search）

从某个状态开始，不断地转移状态直到无法转移，然后退回到前一步的状态，继续转移到其他状态，如此不断重复。

树形图理解

1

2

3

4

5

6

7

8

9

10

11

1→2→3→4→无法转移→返回4的上一节点3（不是直接回1）→5→返回2→6→返回1→7→8→9→返回8→10→返回7→11

（2）与BFS

与 BFS 不同，更早访问的结点可能不是更靠近根结点的结点。因此，你在 DFS 中找到的第一条路径可能不是最短路径。

2.实现

（1）数据结构

这种操作方式很像栈，先进先出，后进后出（LIFO：Last In First Out）。所以我们使用stack栈。

PS：当我们递归地实现 DFS 时，有时似乎不需要使用任何栈。但实际上，我们递归调用DFS()函数就是调用栈（Call Stack）。

所以空间复杂度：

在最坏的情况下，维护系统栈需要 O(h)，其中 h 是 DFS 的最大深度。在计算空间复杂度时，还要考虑系统栈。

（2）伪代码

void dfs()//参数用来表示状态  
{  
    if(到达终点状态)  
    {  
        ...//根据题意添加  
        return;  
    }  
    if(越界或者是不合法状态)
    	...//越界处理
        return;  
    if(特殊状态)
    	...//剪枝
        return ;
    for(扩展方式)  
    {  
        if(扩展方式所达到状态合法)  
        {  
            修改操作;//根据题意来添加  
            标记；  
            dfs（）；  
            (还原标记)；  
            //是否还原标记根据题意  
            //如果加上（还原标记）就是 回溯法  
        }  
 
    }  
}  

3.剪枝

DFS是一种穷竭搜索，它会遍历所有的节点数据，当解空间非常大时，复杂度就会很高，容易超时。

我们就需要做一些优化，如果在进行深度优先遍历时，知道这个节点之后的路径都无法满足要求时，就不再进行这个结点之后所有的路径，这样就减少了遍历的规模。

我们从题目中找到可以优化的规律。比如下面部分和问题，如果限制条件变成0<=ai<=10^8（ai是非负数），意思是部分和只会不变或者递增，不会减小，那么只要sum部分和超过了目标数k的话，之后无论选择什么数都不会让sum等于k，所以就不用继续沿着此节点后的路径搜索。

在优化规律下剪掉

在优化规律下剪掉

1

2

3

不用算4

不用算5

6

7

8

9

10

11

二、树的DFS

1.部分和问题

DFS的简例解析：
https://blog.csdn.net/sandalphon4869/article/details/89361869

三、矩阵迷宫

1.方向向量

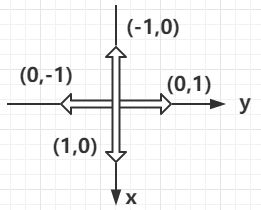
因为方向向量要和迷宫矩阵对应，所以不是随便定上下左右的，上下左右是用来在迷宫中行走的。

比如：我们以迷宫矩阵的左上角为起始坐标（0，0），那么往下走到达（1，0），变化（1，0）矢量；往右走到达（0，1），变化（0，1）矢量；往上走到达（-1，0），变化（-1，0）矢量；往左走到达（0，-1），变化（0，-1）矢量。

矢量（x，y）如下图所示。

int dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};
//四个方向:下，右，上，左

int dir[4][2] = {{1,0},{0,1},{-1,0},{0,-1}};
//下，右，上，左

2.基础

（1）DFS输出螺旋矩阵

灵活理解方向向量
https://blog.csdn.net/sandalphon4869/article/details/95458114

（2）输出迷宫的多条路径

DFS+回溯vis标记数组+stack+路径：
https://blog.csdn.net/sandalphon4869/article/details/89359096

3.进阶

（1）八联通

DFS+将各元素的vis逐渐标记
https://blog.csdn.net/sandalphon4869/article/details/89361903

---

参考：
https://blog.csdn.net/qq_40763929/article/details/81629800