团灭 LeetCode 股票买卖问题
转载自labuladong
作者labuladong
预计阅读时间: 12分钟
上篇文章 用递归的方法实现了一套简单易懂的可行解,但是时间复杂度略高,不能通过全部测试用例。
这篇文章用「状态机」的技巧给出最优解,可以全部提交通过。不要觉得这个名词高大上,文学词汇而已,实际上就是 DP table,等会儿一讲就明白了。
先随便抽一道题出来,看看别人发的解法:
能看懂吧?会做了吧?不可能的,你看不懂,这才正常。就算你勉强看懂了,下一个问题你还是做不出来。那为什么别人能写出这么诡异却又高效的解法呢?因为这类问题是有框架的,但是人家不会告诉你的,因为一旦告诉你,你十分钟就学会了,该算法题就不再神秘,变得不堪一击了。
本文就来告诉你处理这类问题的框架,拒绝奇技淫巧,稳扎稳打,以不变应万变。
这 6 道题目是有共性的,本文通过对第四道题的分析,逐步解决所有问题。因为第四题是一个最泛化的形式,其他的问题都是这个形式的简化。看下题目:
第一题是只进行一次交易,相当于 k = 1;第二题是不限交易次数,相当于 k = +infinity(正无穷);第三题是只进行 2 次交易,相当于 k = 2;剩下两道也是不限交易次数,但是加了交易「冷冻期」和「手续费」的额外条件,其实就是第二题的变种,都很容易处理。
如果你还不熟悉题目,可以去 LeetCode 或者上篇文章
一、穷举框架
首先,还是一样的思路:如何穷举?这里的穷举思路和上篇文章递归的思想不太一样。
递归其实是符合我们思考的逻辑的,一步步推进,遇到无法解决的就丢给递归,一不小心就做出来了,可读性还很好。缺点就是一旦出错,你也不容易找到错误出现的原因。比如上篇文章的递归解法,肯定还有计算冗余,但确实不容易找到。
而这里,我们不用递归思想进行穷举,而是利用「状态」进行穷举。
看看总共有几种「状态」,再找出每个「状态」对应的「选择」。我们要穷举所有「状态」,穷举的目的是根据对应的「选择」更新状态。看图,就是这个意思。
具体到当前问题,每天都有三种「选择」:买入、卖出、无操作,我们用 buy, sell, rest 表示这三种选择。
但问题是,并不是每天都可以任意选择这三种选择的,因为 sell 必须在 buy 之后,buy 必须在 sell 之后(第一次除外)。那么 rest 操作还应该分两种状态,一种是 buy 之后的 rest(持有了股票),一种是 sell 之后的 rest(没有持有股票)。而且别忘了,我们还有交易次数 k 的限制,就是说你 buy 还只能在 k > 0 的前提下操作。
很复杂对吧,不要怕,我们现在的目的只是穷举,你有再多的状态,老夫要做的就是一把梭全部列举出来。这个问题的「状态」有三个,第一个是天数,第二个是当天允许交易的最大次数,第三个是当前的持有状态(即之前说的 rest 的状态,我们不妨用 1 表示持有,0 表示没有持有)。
我们用一个三维数组 dp 就可以装下这几种状态的全部组合,用 for 循环就能完成穷举:
而且我们可以用自然语言描述出每一个状态的含义,比如说 dp[3][2][1] 的含义就是:今天是第三天,我现在手上持有着股票,至今最多进行 2 次交易。再比如 dp[2][3][0] 的含义:今天是第二天,我现在手上没有持有股票,至今最多进行 3 次交易。很容易理解,对吧?
我们想求的最终答案是 dp[n - 1][K][0],即最后一天,最多允许 K 次交易,所能获取的最大利润。读者可能问为什么不是 dp[n - 1][K][1]?因为 [1] 代表手上还持有股票,[0] 表示手上的股票已经卖出去了,很显然后者得到的利润一定大于前者。
记住如何解释「状态」,一旦你觉得哪里不好理解,把它翻译成自然语言就容易理解了。
二、状态转移框架
现在,我们完成了「状态」的穷举,我们开始思考每种「状态」有哪些「选择」,应该如何更新「状态」。
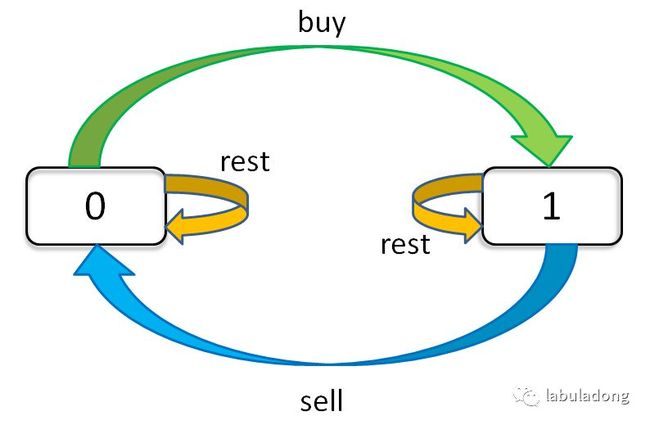
因为我们的选择是 buy, sell, rest,而这些选择是和「持有状态」相关的,所以只看「持有状态」,可以画个状态转移图。
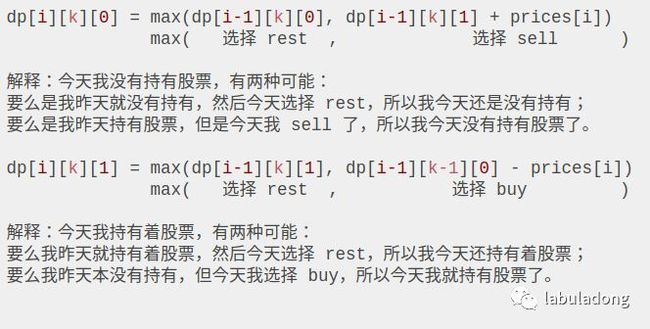
通过这个图可以很清楚地看到,每种状态(0 和 1)是如何转移而来的。根据这个图,我们来写一下状态转移方程:
这个解释应该很清楚了,如果 buy,就要从利润中减去 prices[i],如果 sell,就要给利润增加 prices[i]。今天的最大利润就是这两种可能选择中较大的那个。而且注意 k 的限制,我们在选择 buy 的时候,把最大交易数 k 减小了 1,很好理解吧,当然你也可以在 sell 的时候减 1,一样的。
现在,我们已经完成了动态规划中最困难的一步:状态转移方程。如果之前的内容你都可以理解,那么你已经可以秒杀所有问题了,只要套这个框架就行了。不过还差最后一点点,就是定义 base case,即最简单的情况。
把上面的状态转移方程总结一下:
读者可能会问,这个数组索引是 -1 怎么编程表示出来呢,负无穷怎么表示呢?这都是细节问题,有很多方法实现。现在整体框架已经完成,下面开始具体化。
三、秒杀题目
第一题,k = 1
直接套状态转移方程,根据 base case,可以做一些化简:
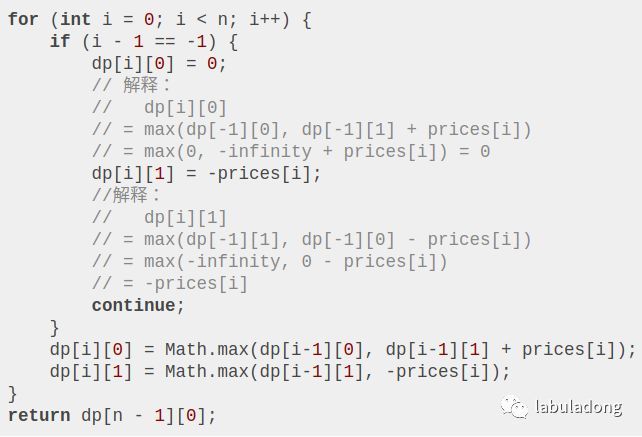
直接翻译成代码:
显然 i = 0 时 dp[i-1] 是不合法的。这是因为我们没有对 i 的 base case 进行处理。那就简单粗暴地处理一下:
第一题就解决了,但是这样处理 base case 很麻烦,而且注意一下状态转移方程,新状态只和相邻的一个状态有关,其实不用整个 dp 数组,只需要两个变量储存所需的状态就足够了,这样可以把空间复杂度降到 O(1):
两种方式都是一样的,不过这种编程方法简洁很多。但是如果没有前面状态转移方程的引导,是肯定看不懂的。后续的题目,我主要写这种空间复杂度 O(1) 的解法。
第二题,k = +infinity
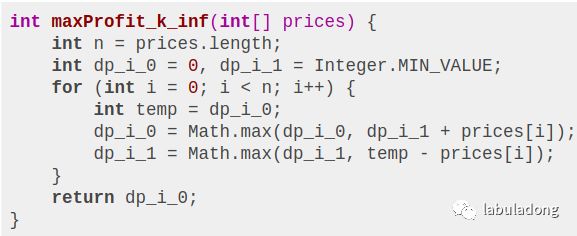
如果 k 为正无穷,那么就可以认为 k 和 k - 1 是一样的。可以这样改写框架:
直接翻译成代码即可:
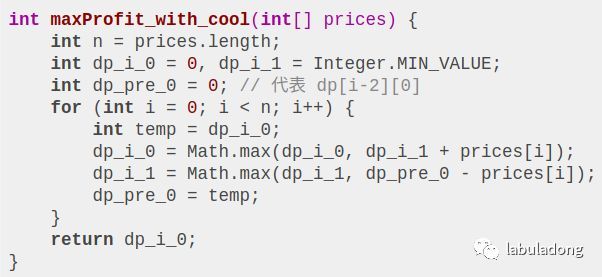
第三题,k = +infinity with cooldown
每次 sell 之后要等一天才能继续交易。只要把这个特点融入上一题的状态转移方程即可:
直接翻译成代码即可:
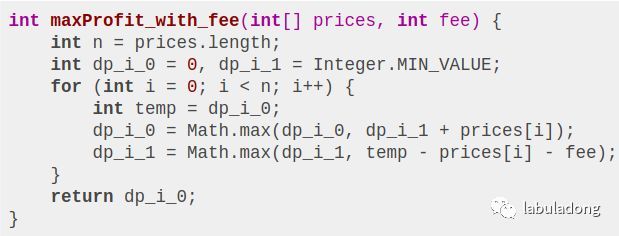
第四题,k = +infinity with fee
每次交易要支付手续费,只要把手续费从利润中减去即可:
直接翻译成代码即可:
第五题,k = 2
k = 2 和前面题目的情况稍微不同,因为上面的情况都和 k 的关系不太大。要么 k 是正无穷,状态转移和 k 没关系了;要么 k = 1,跟 k = 0 这个 base case 挨得近,最后也被消掉了。
这道题 k = 2 和后面要讲的 k 是任意正整数的情况中,对 k 的处理就凸显出来了。我们直接写代码,边写边分析原因。
按照之前的代码,我们可能想当然这样写代码(错误的):
为什么错误?我这不是照着状态转移方程写的吗?
还记得前面总结的「穷举框架」吗?就在强调必须穷举所有状态。其实我们之前的解法,都在穷举所有状态,只是之前的题目中 k 都被化简掉了,所以没有对 k 的穷举。比如说第一题,k = 1:
这道题由于没有消掉 k 的影响,所以必须要用 for 循环对 k 进行穷举才是正确的:
如果你不理解,可以返回第一点「穷举框架」重新阅读体会一下。
第二种解法:因为这里 k 取值范围比较小,所以也可以不用 for 循环,直接把 k = 1 和 2 的情况手动列举出来也是一样的:
有状态转移方程和含义明确的变量名引导,相信你很容易看懂。如我我们想故弄玄虚,可以把上述四个变量换成 a, b, c, d。这样当别人看到你的解法时就会大惊失色,一头雾水,不得不对你肃然起敬。
第六题,k = any integer
这题和 k = 2 没啥区别,可以直接套上一题的第一个解法。但是提交之后会出现一个超内存的错误,原来是传入的 k 值可以任意大,导致 dp 数组太大了。现在想想,交易次数 k 最多能有多大呢?
一次交易由买入和卖出构成,至少需要两天。所以说有效的限制次数 k 应该不超过 n/2,如果超过,就没有约束作用了,相当于 k = +infinity。这种情况是之前解决过的。
直接把之前的代码重用:
至此,6 道题目通过一个状态转移方程全部解决。
四、最后总结
本文给大家讲了如何通过状态转移的方法解决复杂的问题,用一个状态转移方程秒杀了 6 道股票买卖问题,现在想想,其实也不算难对吧?而这已经属于动态规划问题中较困难的了。
关键就在于找到所有可能的「状态」,然后想想怎么更新这些「状态」。一般用一个多维 dp 数组储存这些状态,从 base case 开始向后推进,推进到最后的状态,就是我们想要的答案。想想这个过程,你是不是有点理解「动态规划」这个名词的意义了呢?
具体到股票买卖问题,我们发现了三个状态,使用了一个三维数组,无非还是穷举 + 更新,不过我们可以说的高大上一点,这叫「三维 DP」,怕不怕?这个大实话一说,立刻显得你高人一等有没有?
所以给个在看/分享吧,鼓励一下我。