了解数据分析常用的基本概念

数据统计和数据挖掘

“ 统计 ”,对于大多数人来说不是很陌生,在“ 统计 ”、“ 挖掘 ”这两个概念中,可能大家往往会觉得“ 挖掘 ”更难理解。 统计和挖掘最大的差别在于:统计是事先设想好的一个动作,然后去验证它。 例如先假设销售收入和销售投入之间有关系,公司多投钱给推销人员去拜访客户,就能获得更多的用户和订单,销售收入就能上升,然后我们用统计的模型去验证它。 而数据挖掘是： 在数据中看不到一定的规律，然后从大量数据中通过各种方法（一些算法等）找出隐藏的规律信息。

平均值

平均值基本都明白他是如何计算的,但是平均值的功能是：在数据量大的情况下,平均值反映的是一个数据“ 应该 ”是什么。 例如 ：在一次考试结束后，平均成绩是75.6分，那么每个人就“应该”考到75.6分。

标准差

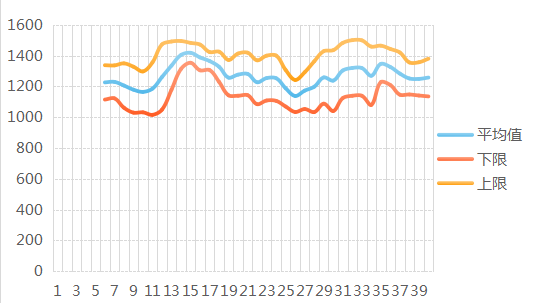
如果说平均值反映了数据的“中轴线”,那么标准差就反映了数据的波动情况,也就是说数据是波澜不惊还是起伏不定。 “ 平均值+标准差 ”仿佛就是一对结义兄弟,焦不离孟、孟不离焦,我们经常用这个组合来衡量数据的变动范围， 如下平均值和标准差的分布图。

正态分布

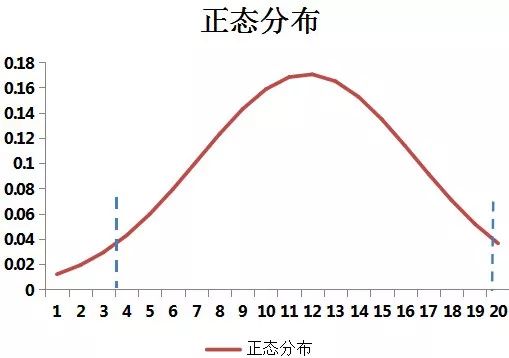
首先看一张图

从上图我们可以总结出规律： “ 中间是凸起的，两边是凹下的，像一个山峰”。

1.两边基本是对称的。

2.形状像一个的“钟”。

3.高峰在中间，越到中间，数据分布概率越大，越到两边，概率越小。

这个看上去很简单的正态分布,其实就是统计分析的重要基础,实际上很多统计规律都是建立在数据正态分布的基础上的。 或者说,如果数据不是正态分布的,那么很多统计规律则是不成立的。

峰度和偏度

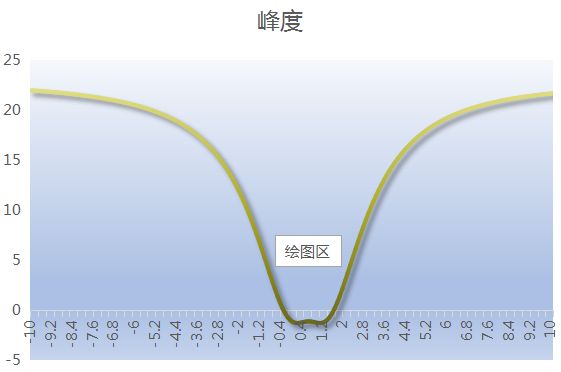
峰度和偏度是数据分析中比较专业的概念了，峰度反映的是数据中极值的情况, 看下图 ：

极值是-10的时候，KURT函数的结果是21.9569，然后看看当极值在-10到10之间的KURT 函数结果图 ：

可以看出,当极值与原值的取值范围比较接近的时候,峰值会接近于0,而极值与原值的范围差距比较大时,峰度值会变大,但是无论是正极值还是负极值,峰度的最大值都是22左右。

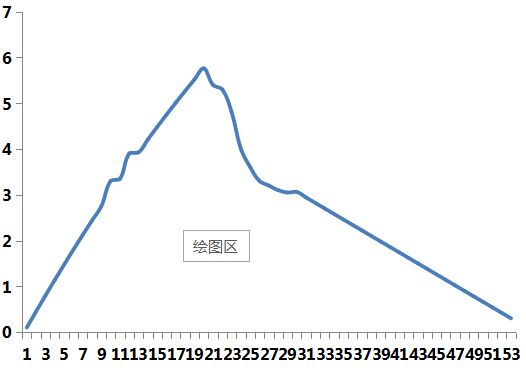
偏度 是衡量数据的对称性的 重要指标 ， Excel 中对应的函数是 SKEW ，它用于比较正态分布的曲线。

左偏度的图 ：

数据明显是偏左的，偏度是0.346382，然后看看右偏度 ：

数据明显右偏，数据的偏度为-0.098。 因此根据偏度值判断 数据

对称性 的规则如下:

• 数据服从正态分布,偏度为0。
• 数据左偏,偏度>0。
• 数据右偏,偏度<0。

连续和离散

连续变量 和 离散变量 是数据分析中经常遇到的， 所谓的连续变量就是变量是在一个区间里面可以任意变化 ，例如： 某个销售员的销售业绩在10w到20w之间，每个值都有可能取到。 离散变量就是只能去几个值，例如： 天气预报的雾霾等级是优、良、中、轻度污染、重度污染。

因变量和自变量

因变量 , 一般指的是我们研究和关心的变量,自变量一般就是其发生变化后会引起其他变量变化的变量 。因变量和自变量说起来很容易,但是在实际的数据分析中,往往会容易混淆。例如：“销售收入和销售费用”在判断因变量和自变量比较简单方法:时间上靠前的就是自变量,时间上靠后的就是因变量。在实际销售工作中,基本都是先有销售费用,然后才有销售收入的,因此销售费用是自变量,销售收入是因变量。