雷诺输运定理的证明
雷诺输运定理的证明
雷诺输运定理描述的是微分符号如何放到求导符号里面的问题,它的一个表述如下:
d d t ∫ Ω ( t ) f d V = ∫ Ω ( t ) ∂ f ∂ t d V + ∫ ∂ Ω ( t ) ( v ⋅ n ) f d A \frac{\mathrm{d}}{\mathrm{d} t} \int_{\Omega(t)} \mathbf{f} \mathrm{d} \mathrm{V}=\int_{\Omega(t)} \frac{\partial \mathbf{f}}{\partial t} \mathrm{d} \mathrm{V}+\int_{\partial \Omega(t)}\left(\mathbf{v} \cdot \mathbf{n}\right) \mathbf{f} \mathrm{d} \mathrm{A} dtd∫Ω(t)fdV=∫Ω(t)∂t∂fdV+∫∂Ω(t)(v⋅n)fdA
其中的 Ω ( t ) \Omega(t) Ω(t)是边界变化的一个区域,物理量 f \mathbf{f} f可以是向量或者标量, v \mathbf{v} v是某一点的速度, n \mathbf{n} n是区域表明的单位外法向量。
下面给一个简单的证明。
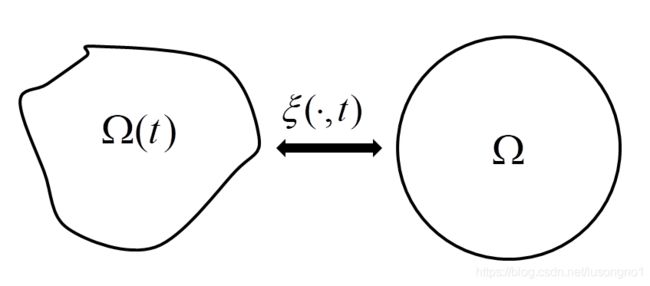
不妨假设 f \mathbf{f} f为标量,即令 f = ρ ( x , t ) \mathbf{f} = \rho(x,t) f=ρ(x,t)。我们可以通过一个变换,将时变的区域都变换到一个和时间无关的标准区域,即令 x = ξ ( x ~ , t ) x=\xi(\tilde x,t) x=ξ(x~,t), x ~ \tilde x x~是标准区域上的空间变量。这个标准区域长什么样子没有太大关系,因为变过去,最后还要变回来。
那么有(为了书写的简洁方便,可能在公式中会将雅克比行列式写为 J J J,以及省略掉比较明显的函数自变量):
d d t ∫ Ω ( t ) ρ ( x , t ) d x = d d t ∫ Ω ρ ( ξ ( x ~ , t ) , t ) ∣ ξ x ~ ∣ d x ~ = ∫ Ω d d t ( ρ ( ξ ( x ~ , t ) , t ) ∣ ξ x ~ ∣ ) d x ~ = ∫ Ω J d ρ d t + ρ d J d t d x ~ = ∫ Ω J ( ∂ ρ ∂ t + v ⋅ ∇ ρ ) + ρ ( ∇ ⋅ v ⋅ J ) d x ~ = ∫ Ω J ∂ ρ ∂ t + J ∇ ⋅ ( ρ v ) d x ~ = ∫ Ω ( t ) ∂ ρ ∂ t + ∇ ⋅ ( ρ v ) d x = ∫ Ω ( t ) ∂ ρ ∂ t d x + ∫ ∂ Ω ( t ) ( ρ v ⋅ n ) d s \frac{\mathrm{d}}{\mathrm{d} t} \int_{\Omega(t)} \rho(x,t)\mathrm{d} x=\frac{\mathrm{d}}{\mathrm{d} t} \int_{\Omega} \rho(\xi(\tilde x,t),t)|\xi_{\tilde x}|\mathrm{d} \tilde x = \int_{\Omega} \frac{\mathrm{d}}{\mathrm{d} t} ( \rho(\xi(\tilde x,t),t)|\xi_{\tilde x}|)\mathrm{d} \tilde x\\= \int_\Omega J\frac{\mathrm{d \rho}}{\mathrm{dt}}+ \rho\frac{\mathrm{d J}}{\mathrm{dt}}\mathrm{d} \tilde x= \int_\Omega J(\frac{\partial \rho}{\partial t}+\mathbf{v}\cdot \nabla \rho)+ \rho(\nabla \cdot \mathbf{v}\cdot J) \mathrm{d} \tilde x\\= \int_\Omega J\frac{\partial \rho}{\partial t}+J \nabla \cdot (\rho \mathbf{ v}) \mathrm{d} \tilde x= \int_{\Omega(t)} \frac{\partial \rho}{\partial t}+\nabla \cdot (\rho \mathbf{ v}) \mathrm{d} x = \int_{\Omega(t)} \frac{\partial \rho}{\partial t} \mathrm{d} x + \int_{\partial \Omega(t)} (\rho \mathbf{ v}\cdot \mathbf{n}) \mathrm{d} s dtd∫Ω(t)ρ(x,t)dx=dtd∫Ωρ(ξ(x~,t),t)∣ξx~∣dx~=∫Ωdtd(ρ(ξ(x~,t),t)∣ξx~∣)dx~=∫ΩJdtdρ+ρdtdJdx~=∫ΩJ(∂t∂ρ+v⋅∇ρ)+ρ(∇⋅v⋅J)dx~=∫ΩJ∂t∂ρ+J∇⋅(ρv)dx~=∫Ω(t)∂t∂ρ+∇⋅(ρv)dx=∫Ω(t)∂t∂ρdx+∫∂Ω(t)(ρv⋅n)ds
即证。
注意到,这个过程中,我们用到了物质导数以及对行列式求导的公式 d J / d t = ∇ ⋅ v ⋅ J {\mathrm{d}J}/{dt}=\nabla \cdot \mathbf{v}\cdot J dJ/dt=∇⋅v⋅J。
事实上,容易验证:
∂ J ( x ~ , t ) ∂ t = ∂ ∂ t ( det F ) = ( det F ) ( ∇ ⋅ v ) = J ( x ~ , t ) ∇ ⋅ v ( ξ ( x ~ , t ) , t ) = J ( x ~ , t ) ∇ ⋅ v ( x ~ , t ) \frac{\partial J(\mathbf{\tilde x}, t)}{\partial t}=\frac{\partial}{\partial t}(\operatorname{det} \boldsymbol{F})=(\operatorname{det} \boldsymbol{F})(\boldsymbol{\nabla} \cdot \mathbf{v})=J(\mathbf{\tilde x}, t) \boldsymbol{\nabla} \cdot \mathbf{v}(\xi(\mathbf{\tilde x}, t), t)=J(\mathbf{\tilde x}, t) \boldsymbol{\nabla} \cdot \mathbf{v}(\mathbf{\tilde x}, t) ∂t∂J(x~,t)=∂t∂(detF)=(detF)(∇⋅v)=J(x~,t)∇⋅v(ξ(x~,t),t)=J(x~,t)∇⋅v(x~,t)
F \mathbf{F} F为雅克比矩阵。