Redis跳跃表源码解析

跳跃表是一种有序的数据结构，支持平均O(logN)、最坏O(N)复杂度的节点查找。跳跃表应用在有序集合键和集群节点的场景上。本文参考Redis3.0版本的源码，注释参考了黄建宏的注释，并加上自己的理解。对于跳跃表和节点的定义是在redis.h中，而常用API的实现是在t_zset.c中。

定义：

/*
 * 跳跃表
 */
typedef struct zskiplist {

    // 表头节点和表尾节点
    struct zskiplistNode *header, *tail;

    // 表中节点的数量，不包含头节点
    unsigned long length;

    // 表中层数最大的节点的层数，不包含头节点
    int level;

} zskiplist;

/* ZSETs use a specialized version of Skiplists */
/*
 * 跳跃表节点
 */
typedef struct zskiplistNode {

    // 成员对象
    robj *obj;

    // 分值
    double score;

    // 后退指针
    struct zskiplistNode *backward;

    // 层
    struct zskiplistLevel {

        // 前进指针
        struct zskiplistNode *forward;

        // 跨度
        unsigned int span;

    } level[];

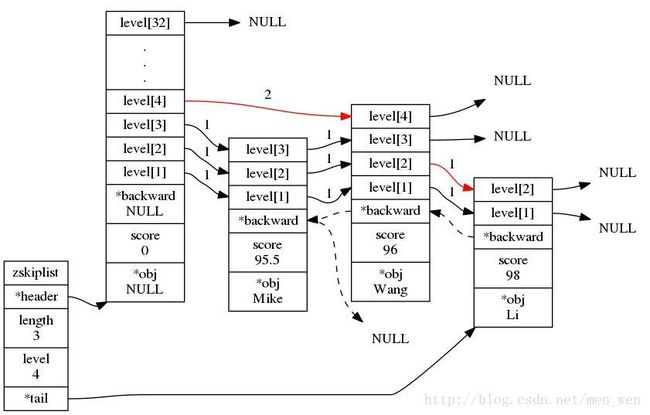
} zskiplistNode;

以下为一个可能的跳跃表示例：

新建：zslCreate

/*
 * 创建并返回一个新的跳跃表
 *
 * T = O(1)
 */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    // 分配空间
    zsl = zmalloc(sizeof(*zsl));

    // 设置高度和起始层数
    zsl->level = 1;
    zsl->length = 0;

    // 初始化表头节点
    // T = O(1)
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;

    // 设置表尾
    zsl->tail = NULL;

    return zsl;
}

/*
 * 创建一个层数为 level 的跳跃表节点，
 * 并将节点的成员对象设置为 obj ，分值设置为 score 。
 *
 * 返回值为新创建的跳跃表节点
 *
 * T = O(1)
 */
zskiplistNode *zslCreateNode(int level, double score, robj *obj) {
    
    // 分配空间
    zskiplistNode *zn = zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));

    // 设置属性
    zn->score = score;
    zn->obj = obj;

    return zn;
}

插入：最为核心的API

/*
 * 创建一个成员为 obj ，分值为 score 的新节点，
 * 并将这个新节点插入到跳跃表 zsl 中。
 * 
 * 函数的返回值为新节点。
 */
zskiplistNode *zslInsert(zskiplist *zsl, double score, robj *obj) {
    //这个update很巧妙，记录了离插入位置最近的那个节点，保存的是level[i].forward
    //如果在跳跃表上跟踪记录轨迹，则是竖折形状。
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x; //32
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    redisAssert(!isnan(score));

    // 在各个层查找节点的插入位置
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {

        /* store rank that is crossed to reach the insert position */
        // rank[i]用来记录第i层达到插入位置的所跨越的节点总数,也就是该层最接近(小于)给定score的排名 
        // rank[0]则是离插入位置最近的节点的rank，是前面每一层最终的累加值
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];

        // 沿着前进指针遍历跳跃表
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                // 比对分值
                (x->level[i].forward->score == score &&
                // 比对成员， T = O(N)
                compareStringObjects(x->level[i].forward->obj,obj) < 0))) {

            // 记录沿途跨越了多少个节点
            rank[i] += x->level[i].span;

            // 移动至下一指针
            x = x->level[i].forward;
        }
        // 记录将要和新节点相连接的节点
        update[i] = x;
    }

    /* we assume the key is not already inside, since we allow duplicated
     * scores, and the re-insertion of score and redis object should never
     * happen since the caller of zslInsert() should test in the hash table
     * if the element is already inside or not. 
     *
     * zslInsert() 的调用者会确保同分值且同成员的元素不会出现，
     * 所以这里不需要进一步进行检查，可以直接创建新元素。
     */

    // 获取一个随机值作为新节点的层数
    // T = O(N)
    level = zslRandomLevel();

    // 如果新节点的层数比表中其他节点的层数都要大
    // 那么初始化表头节点中未使用的层，并将它们记录到 update 数组中
    // 将来也指向新节点
    if (level > zsl->level) {

        // 初始化未使用层
        // T = O(1)
        for (i = zsl->level; i < level; i++) {
            rank[i] = 0;
            //初始化头节点中未触及到的区间[zsl->level,level)
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length; //这个没看明白
        }

        // 更新表中节点最大层数
        zsl->level = level;
    }

    // 创建新节点
    x = zslCreateNode(level,score,obj);

    // 将前面记录的指针指向新节点，并做相应的设置
    // T = O(1)
    for (i = 0; i < level; i++) {
        
        // 设置新节点的 forward 指针
        x->level[i].forward = update[i]->level[i].forward;
        
        // 将沿途记录的各个节点的 forward 指针指向新节点
        update[i]->level[i].forward = x;
        
        /* update span covered by update[i] as x is inserted here */
        // 计算新节点跨越的节点数量
        // 未插入前顺序：update[i]..update[0]   插入x后顺序: update[i]..update[0]..x  
        // rank[0]-rank[i]表示的是update[i]和update[0]之间的跨度span
        // update[i]->level[i].span表示的是update[i]与update[i]->level[i]->forward之间的span 
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);

        // 更新新节点插入之后，沿途节点的 span 值
        // 其中的 +1 计算的是新节点，表示时从update[i]->level[i]到x的span
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    }

    /* increment span for untouched levels */
    //如果新节点的level小于跳跃表的最大层数，未接触的节点的 span 值也需要增一，因为横跨在新节点上方，这些节点直接从表头指向新节点
    // T = O(1)
    for (i = level; i < zsl->level; i++) {
        update[i]->level[i].span++;
    }

    // 设置新节点的后退指针
    // 新节点可能直接插在头节点的后面，这种情况下update[0]为header
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    // 插入位置是否插入尾节点
    if (x->level[0].forward) 
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;

    // 跳跃表的节点计数增一
    zsl->length++;

    return x;
}

/* Returns a random level for the new skiplist node we are going to create.
 *
 * 返回一个随机值，用作新跳跃表节点的层数。
 *
 * The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
 * (both inclusive), with a powerlaw-alike distribution where higher
 * levels are less likely to be returned. 
 *
 * 返回值介乎 1 和 ZSKIPLIST_MAXLEVEL 之间（包含 ZSKIPLIST_MAXLEVEL），
 * 根据随机算法所使用的幂次定律，越大的值生成的几率越小。
 *
 * T = O(N)
 */
int zslRandomLevel(void) {
    int level = 1;

    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;

    return (level

特别注意的是，这个层数创建时是根据幂次定律来随机生成一个1-32之间的值。具体算法参见随机算法。

删除

/* Delete an element with matching score/object from the skiplist. 
 *
 * 从跳跃表 zsl 中删除包含给定节点 score 并且带有指定对象 obj 的节点。
 *
 * T_wrost = O(N^2), T_avg = O(N log N)
 */
int zslDelete(zskiplist *zsl, double score, robj *obj) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    // 遍历跳跃表，查找目标节点，并记录所有沿途节点
    // T_wrost = O(N^2), T_avg = O(N log N)
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {

        // 遍历跳跃表的复杂度为 T_wrost = O(N), T_avg = O(log N)
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                // 比对分值
                (x->level[i].forward->score == score &&
                // 比对对象，T = O(N)
                compareStringObjects(x->level[i].forward->obj,obj) < 0)))

            // 沿着前进指针移动
            x = x->level[i].forward;

        // 记录沿途节点
        update[i] = x;
    }

    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. 
     *
     * 检查找到的元素 x ，只有在它的分值和对象都相同时，才将它删除。
     */
    x = x->level[0].forward;
    if (x && score == x->score && equalStringObjects(x->obj,obj)) {
        // T = O(1)
        zslDeleteNode(zsl, x, update);
        // T = O(1)
        zslFreeNode(x);
        return 1;
    } else {
        return 0; /* not found */
    }

    return 0; /* not found */
}

内部删除：

/* Internal function used by zslDelete, zslDeleteByScore and zslDeleteByRank 
 * 
 * 内部删除函数，
 * 被 zslDelete 、 zslDeleteRangeByScore 和 zslDeleteByRank 等函数调用。
 *
 * T = O(1)
 * 输入update为与删除节点x相关的前置节点数组，与插入操作的中的update类似
 */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;

    // 更新所有和被删除节点 x 有关的节点的指针，解除它们之间的关系
    // 两种情况:
    // (1)与删除节点x直接相连的：相加减1
    // (2)横跨删除节点的：直接减1
    // T = O(1)
    for (i = 0; i < zsl->level; i++) {
        if (update[i]->level[i].forward == x) {
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        } else {
            update[i]->level[i].span -= 1;
        }
    }

    // 更新被删除节点 x 的前进和后退指针：非尾节点和尾节点分别处理
    if (x->level[0].forward) {
        x->level[0].forward->backward = x->backward;
    } else {
        zsl->tail = x->backward;
    }

    // 更新跳跃表最大层数（只在被删除节点是跳跃表中最高的节点时才执行）
    // T = O(1)
    // 遍历头节点的level数组，直到找到第一个前进指针不为NULL的
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;

    // 跳跃表节点计数器减一
    zsl->length--;
}

zslGetRank：

/* Find the rank for an element by both score and key.
 *
 * 查找包含给定分值和成员对象的节点在跳跃表中的排位。
 *
 * Returns 0 when the element cannot be found, rank otherwise.
 *
 * 如果没有包含给定分值和成员对象的节点，返回 0 ，否则返回排位。
 *
 * Note that the rank is 1-based due to the span of zsl->header to the
 * first element. 
 *
 * 注意，因为跳跃表的表头也被计算在内，所以返回的排位以 1 为起始值。
 *
 * T_wrost = O(N), T_avg = O(log N)
 */
unsigned long zslGetRank(zskiplist *zsl, double score, robj *o) {
    zskiplistNode *x;
    unsigned long rank = 0;
    int i;

    // 遍历整个跳跃表
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {

        // 遍历节点并对比元素
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                // 比对分值
                (x->level[i].forward->score == score &&
                // 比对成员对象
                compareStringObjects(x->level[i].forward->obj,o) <= 0))) {

            // 累积跨越的节点数量
            rank += x->level[i].span;

            // 沿着前进指针遍历跳跃表
            x = x->level[i].forward;
        }

        /* x might be equal to zsl->header, so test if obj is non-NULL */
        // x可能为空节点，需要进行非空判断。必须确保不仅分值相等，而且成员对象也要相等
        // T = O(N)
        if (x->obj && equalStringObjects(x->obj,o)) {
            return rank;
        }
    }

    // 没找到
    return 0;
}

参考文献：

https://blog.csdn.net/men_wen/article/details/70040026

https://blog.csdn.net/kisimple/article/details/38706729

http://makaidong.com/yongning99/1/88707_10585499.html