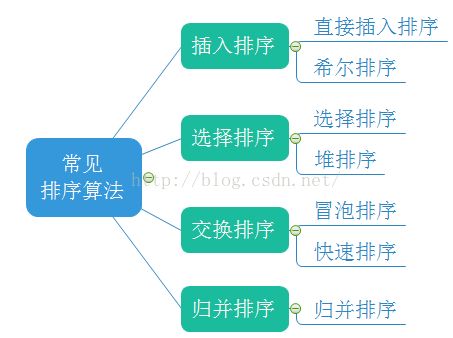
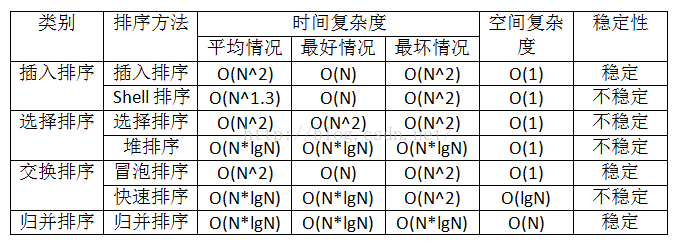
各类排序算法的对比及实现

这里所有的实现都是以升序为例，这里是探讨排序的算法，为了简洁，全部都用int,暂不考虑在定义类型

直接插入排序：

直接排序就是假定前面的数都是有序的，然后将一个数插入到前面有序的这个序列中，当从第一个开始时，就保证了这个数组要排序的数的前面的序列都是有序的

void InsertSort(int* a, size_t size)//直接插入函数
{
	assert(a);//参数入口检测
	for (size_t j = 1; j < size; j++)//循环条件保证了每个数都进行了插入
	{
		size_t i = 0;
		while (ia[i])//循环条件ii; index--)//将a[i]后面的从i到j整体向后踢动一位
		{
			a[index] = a[index - 1];
		}
		a[i] = tmp;//将啊a[j]放到它应该插入的位置
	}
}

希尔排序：

是直接插入排序算法的一种更高效的改进版本，希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

void ShellSort(int *a, size_t size)
{
	assert(a);
	int spilk = size;//增量定义
	while (spilk >1)//当增量大于1时，进入循环，增量最小为1
	{
		spilk = spilk / 3 + 1;//
		for (size_t i = 0; i < size; i++)//保证每个数都进行比较了
		{
			for (size_t j = 0; j + spilk < size; j += spilk)
			{
				if (a[j]>a[j + spilk])
				{
					swap(a[j], a[j + spilk]);
				}
			}
		}
	}
}

选择排序：

选择排序是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

void SelectSort(int *a,size_t size)
{
	assert(a);
	for (size_t i = 0; i < size; i++)//循环size次，确保每个数都被比较了
	{
		int cmp = 0;
		for (size_t j = 0; j < size-i; j++)//每次找到一个最大数放在size-1-i的位置
		{
			if (a[cmp] < a[j])
			{
				cmp = j;
			}
		}
		swap(a[size -1- i], a[cmp]);
	}
}

堆排序：

堆排序是指利用堆积树（堆）这种数据结构所设计的一种排序算法，用大 堆的方式每次找到一个做大的数即堆的第一个结点将它依次从后往前放

void AdjustDown(int *a, size_t k, int root)//下调，将小的数往小调，保证根节点的值为最大值         
{
	size_t parent = root;
	size_t child = parent * 2 + 1;
	while (child < k)
	{
		if (child + 1 < k && a[child] < a[child + 1])
		{
			child++;
		}
		if (a[child] > a[parent])
		{
			swap(a[child], a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapSort(int *a, size_t size)
{
	assert(a);
	for (int i = (size - 2) / 2; i >= 0;i--)
	{
		AdjustDown(a, size, i);//构建大堆
	}
	for (size_t i = 0; i < size; i++)
	{
		swap(a[0], a[size - 1 - i]);//将根依次从最后往前交换
		AdjustDown(a, size-1-i, 0);  //将a[0]进行下调
	}
}

冒泡排序：

比较相邻的元素。如果第一个比第二个大，就交换他们两个。对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。针对所有的元素重复以上的步骤，除了最后一个。持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

void BubbleSort(int *a, size_t size)
{
	assert(a);
	int count = 0;
	for (size_t i = 0; i < size-1; i++)//循环条件保证每个数都被比较
	{
		for (size_t j = 0; j < size -1- i; j++)//循环的次数根据i的变化而不同，每次-1
		{
			if (a[j]>a[j + 1])//比较相邻的两个数
			{
				swap(a[j], a[j + 1]);
				count++;
			}
		}
		if (count == 0)//当一次交换都没有的时候，序列有序，跳出循环
		{
			break;
		}
	}
}

快速排序：

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

//[]
int Getkey(int *a, size_t left,size_t right)
{
	assert(a);
	int mid = left + (right - left) / 2;  //取头，尾，中间三个进行比较，取中间的数返回
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])  // 条件：a[left] < a[mid] && a[mid] < a[right]
		{
			return mid;
		}
		else if (a[left] < a[right]) // 条件：a[left] < a[mid] && a[mid] > a[right] && a[left] < a[right]
		{
			return right;
		}
		else   // 条件：a[left] < a[mid] && a[mid] > a[right] && a[left] > a[right]
			return left;
	}
	else
	{
		if (a[left] < a[right])  //条件：a[left] > a[mid] && a[left] < a[right]
		{
			return left;
		}
		else if (a[mid]>a[right])//条件：a[left] > a[mid] && a[left] > a[right] && a[mid] > a[right]
		{
			return mid;
		}
		else   //条件：a[left] > a[mid] && a[left] > a[right] && a[mid] < a[right]
			return right;
	}
}
//[]
void quicksort(int *a, size_t left, size_t right)
{ 
	if (left < right)  //当数组a有一个是不进行排序与递归
	{
		int key = Getkey(a, left, right);//或取合理的key值
		swap(a[key], a[right]);
		size_t cur = left;
		int index = left;
		while (cur < right) //让cur从left开始往后走,遇到比key大的数就从left开始向后依次交换
		{
			if (a[cur] < a[right])
			{
				swap(a[index++], a[cur]);
			}
			cur++;
		}
		swap(a[index], a[right]);
		quicksort(a, left, index - 1);//左边递归
		quicksort(a, index + 1, right);//右边递归
	}
	else
	{
		return;
	}
}
void QuickSort(int *a, size_t size)
{
	quicksort(a, 0, size - 1);
}

归并排序：

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

void mergersort(int *a, size_t left, size_t right)
{
	size_t mid = left+(right-left) / 2;
	if (right-left>1)
	{
		mergersort(a, left,mid);
		mergersort(a, mid +1,right);
	}
	if (right - left <= 1)
	{
		if (a[left] > a[right])
		{
			swap(a[left], a[right]);
		}
	}
	else
	{
		size_t cur = left;
		size_t cmp = mid+1;
		int i = left;
		int *str = new int[right + 1];
		while (cur <= mid &&  cmp <= right)
		{
			if (a[cur] < a[cmp])
			{
				str[i++] = a[cur++];
			}
			else
			{
				str[i++] = a[cmp++];
			}
		}
		if (cur == mid+1)
		{
			while (cmp <= right)
			{
				str[i++] = a[cmp++];
			}
		}
		else
		{
			while (cur <= mid)
			{
				str[i++] = a[cur++];
			}
		}
		for (size_t i = left; i <= right; i++)
		{
			a[i] = str[i];
		}
		delete[] str;
	}	
}
void MergerSort(int *a, size_t size)
{
	mergersort(a, 0, size - 1);
}

非比较排序：

计数排序：

计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范

围），快于任何比较排序算法。

算法思想：

计数排序对输入的数据有附加的限制条件：

1、输入的线性表的元素属于有限偏序集S；

2、设输入的线性表的长度为n，|S|=k（表示集合S中元素的总数目为k），则k=O(n)。

在这两个条件下，计数排序的复杂性为O(n)。

计数排序的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确

定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位

置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。

void CountingSort(int *a,size_t size)
{
	assert(a);
	if (size < 1)
	{
		return;
	}
	int *countarr = new int[size];
	int *start = new int[size];
	memset(countarr, 0, size*4);
	memset(start, 0, size*4);

	for (size_t i = 0; i < size; i++)
	{
		countarr[a[i]]++;
	}
	for (size_t i = 1; i < size; i++)
	{
		start[i] = start[i - 1] + countarr[i - 1];
	}
	int cur = 0;
	for (size_t i = 0; i < size; i++)
	{
		countarr[start[a[i]]++] = a[i];
	}
	memcpy(a, countarr, size * 4);
	delete[]countarr;
	delete[]start;
}

基数排序：

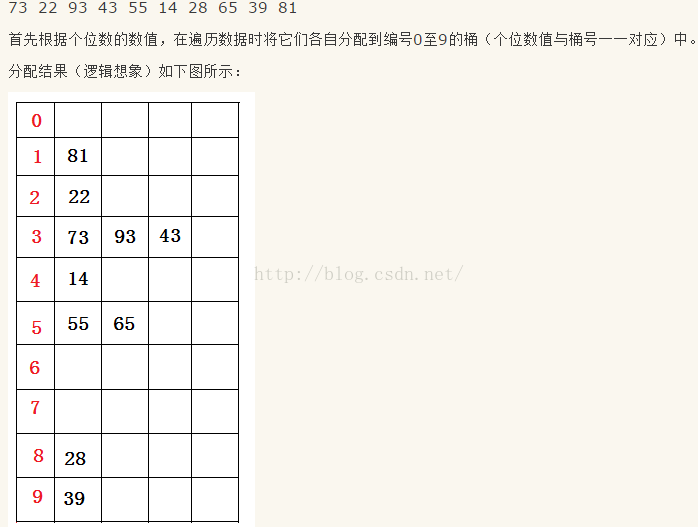
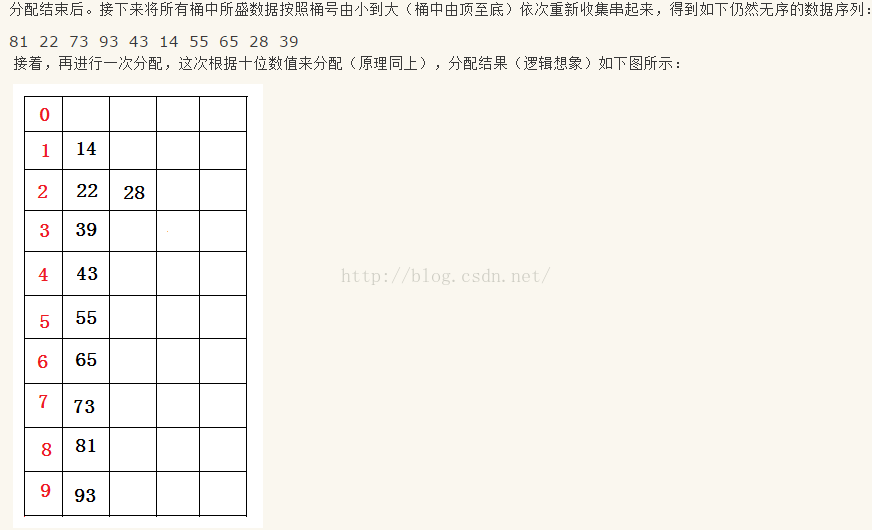
基数排序属于“分配式排序”，又称“桶子法”或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定

性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

算法分析：

代码：

void CountingSorttest()
{
	int a[] = { 5, 2, 4, 3, 9, 7, 6, 8, 1, 0 };
	CountingSort(a, sizeof(a) / sizeof(a[0]));
	display(a, sizeof(a) / sizeof(a[0]));
}

void RadixSort(int *a, size_t size)
{
	int *bucket[10];
	for (size_t i = 0; i < 10; i++)
	{
		bucket[i] = new int[size+1];
	}
	int count = 0;
	for (int i = 0; i < size; i++)
	{
		if (count < a[i])
		{
			count = i;
		}
	}
	int tmp = 0;
	while (count)
	{
		for (int i = 0; i < 10; i++)
		{
			memset(bucket[i], 0, (size+1) * 4);
		}
		for (int i = 0; i < size; i++)
		{
			if (tmp == 0)
			{
				bucket[a[i] % 10][bucket[a[i] % 10][0]++ + 1] = a[i];
			}
			else
			{
				bucket[(a[i] / 10) % 10][bucket[(a[i] / 10) % 10][0]++ + 1] = a[i];
			}
			
		}
		int cur = 0;
		for (int i = 0; i < 10; i++)
		{
			for (int j = 1; j <= bucket[i][0];j++)
			{
				a[cur++] = bucket[i][j];
			}
		}
		count = count / 10;
		tmp++;
	}
}