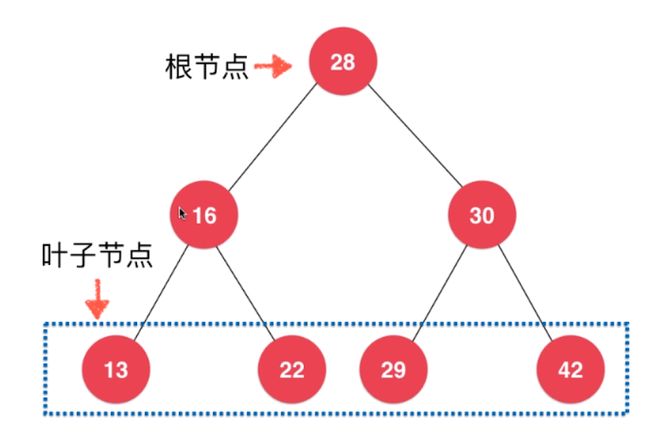
一.二叉树
- 和链表一样,动态数据结构
- class Node{
E e;
Node left;←左孩子
Node right;→右孩子
} - 二叉树具有唯一根节点
- 二叉树每个节点最多有两个子节点
- 每个子节点最多有一个父节点
- 没有子节点的节点称为叶子节点
- 唯一没有父节点的节点为根节点
- 二叉树具有天然的递归结构
- 如果左孩子也是一个二叉树的根节点,我们可以称它为左子树
- 如果右孩子也是一个二叉树的根节点,我们可以称它为右子树
- 每个节点的左子树也是二叉树
- 每个节点的右子树也是二叉树
- 二叉树不一定是满的
- 一个节点也可以看做二叉树
-
Null 空也可以看做二叉树
二. 二分搜索树
- 二分搜索树是二叉树。
- 二分搜索树的每个节点的值:
- 大于其左子树的所有节点的值
- 小于其右子树的所有节点的值
- 每一颗子树也是二分搜索树
- 储存的元素必须具有可比性
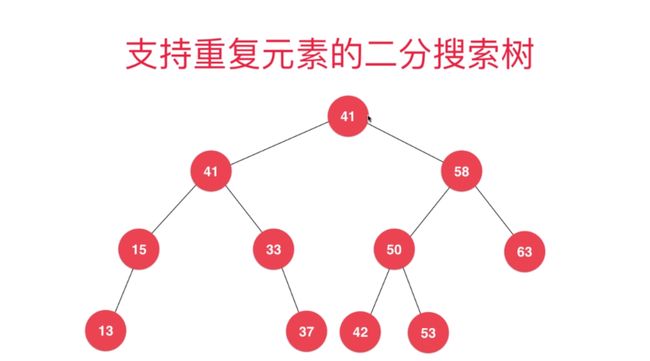
- 我们定义的二分搜索树不包含重复元素
-
如果想要包含重复元素,只需要定义左子树小于等于节点,或者右子树大于等于节点
-
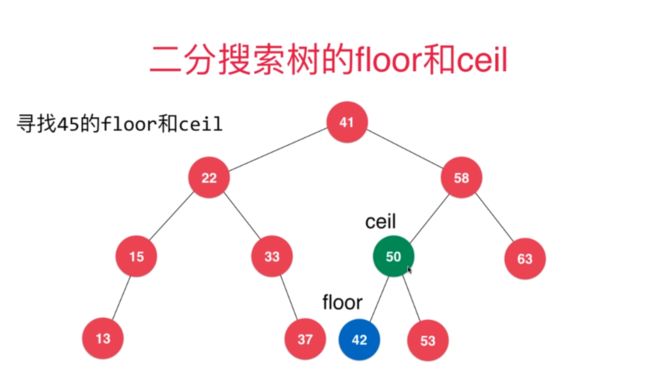
二分搜索树的floor和ceil:
45的floor:比45小的最大整数,45的ceil:比45大的最小整数
三.二分搜索树代码实现
package data_structure;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class BinarySearchTree> {
private int size;
private Node root;
public BinarySearchTree() {
this.size = 0;
this.root = null;
}
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
// public void add (E e){
// if(root==null){
// root=new Node(e);
// size++;
// }else {
// add(root,e);
// }
// }
/**
* 向二分搜索树插入元素
*/
public void add(E e) {
root = add2(root, e);
}
private void add(Node n, E e) {
if (n.e.compareTo(e) > 0) {
if (n.left == null) {
n.left = new Node(e);
size++;
} else {
add(n.left, e);
}
} else if (n.e.compareTo(e) < 0) {
if (n.right == null) {
n.right = new Node(e);
size++;
} else {
add(n.right, e);
}
}
}
/**
* 对add (Node n, E e) 简化 递归遍历插入
*/
private Node add2(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (node.e.compareTo(e) > 0) {
node.left = add2(node.left, e);
} else if (node.e.compareTo(e) < 0) {
node.right = add2(node.right, e);
}
return node;
}
/**
* 查看二分搜索树是否包含元素
*/
public boolean contains(E e) {
return contains(root, e);
}
/**
* 以node 为根的二分搜索树是否包含元素e,递归算法
*/
private boolean contains(Node node, E e) {
if (node == null) {
return false;
}
if (node.e.compareTo(e) > 0) {
return contains(node.left, e);
} else if (node.e.compareTo(e) < 0) {
return contains(node.right, e);
}
return true;
}
/** ------------------------------------------------------------------------深度优先遍历----------------------------------------------------------------- */
/**
* 前序遍历:遍历顺序规则为【根左右】
*/
public void preOrder() {
preOrder(root);
}
/**
* 前序遍历非递归遍历
*/
public void preOrderNR() {
Stack stack = new Stack<>();
if (root != null) {
stack.push(root);
} else {
return;
}
while (!stack.isEmpty()) {
Node curr = stack.pop();
System.out.print(curr.e + " ");
//栈先进后出所以先放右子树,再放左子树
if (curr.right != null) {
stack.push(curr.right);
}
if (curr.left != null) {
stack.push(curr.left);
}
}
}
private void preOrder(Node node) {
if (node == null) {
return;
}
//先对根操作
System.out.print(node.e + " ");
//再对左子树操作
preOrder(node.left);
//再对右子树操作
preOrder(node.right);
}
/**
* 中序遍历: 遍历顺序规则为【左根右】 输出的就是二分搜索树排序后的结果从小到大
*/
public void inOrder() {
inOrder(root);
}
private void inOrder(Node node) {
if (node == null) {
return;
}
inOrder(node.left);
System.out.print(node.e + " ");
inOrder(node.right);
}
/**
* 后序遍历:遍历顺序规则为【左右根】也就是说先处理完孩子节点再处理节点本身 其应用:释放内存(也是先释放子对象内存,后释放父对象内存)
*/
public void postOrder() {
postOrder(root);
}
private void postOrder(Node node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.print(node.e + " ");
}
/**--------------------------------------------------------------------------------------------------------------------------------------------------------- */
/**--------------------------------------------------------------------------广度优先遍历(层序遍历)----------------------------------------------*/
/**
* 层序遍历 能更快地找到想要找到的元素 常用于算法设计中:最短路径
*/
public void extentOrder() {
//使用的队列
Queue queue = new LinkedList<>();
if (root != null) {
queue.add(root);
} else {
return;
}
while (!queue.isEmpty()) {
Node curr = queue.remove();
System.out.println(curr.e);
//因为是队列所以先进先出,先放左子树再放右子树
if (curr.left != null) {
queue.add(curr.left);
}
if (curr.right != null) {
queue.add(curr.right);
}
}
}
/**--------------------------------------------------------------------------------寻找最小最大元素--------------------------------------------------------------*/
/**
* 找最小节点
*/
public E minimum() {
if (size == 0) {
throw new IllegalArgumentException("BinarySearchTree is Empty");
}
Node minimum = minimum(root);
return minimum.e;
}
/**
* 递归的查找左子树为null的节点,左子树为null的节点就是最小值
*/
private Node minimum(Node node) {
if (node.left == null) {
return node;
}
return minimum(node.left);
}
/**
* 非递归查找最小值
*/
public E minimumNR() {
if (size == 0) {
throw new IllegalArgumentException("BinarySearchTree is Empty");
}
Node curr = root;
while (curr.left != null) {
curr = curr.left;
}
return curr.e;
}
/**
* 移除最小节点
* @return
*/
public E removeMinimum(){
E minimum = minimum();
root=removeMinimum(root);
return minimum;
}
/**
* 移除最小节点 返回移除最小节点后的根节点
* @param node
* @return
*/
private Node removeMinimum(Node node){
if(node.left==null){
Node rightNode=node.right;
node.right=null;
size--;
return rightNode;
}
node.left=removeMinimum(node.left);
return node;
}
/**
* 查找最大值
* @return
*/
public E maximum() {
if (size == 0) {
throw new IllegalArgumentException("BinarySearchTree is Empty");
}
return maximum(root).e;
}
/**
* 递归查找最大节点,右子树为null的节点就是最大节点
* @param node
* @return
*/
private Node maximum(Node node) {
if(node.right==null){
return node;
}
return maximum(node.right);
}
/**
* 非递归查找最大节点
* @return
*/
public E maximumNR(){
if (size == 0) {
throw new IllegalArgumentException("BinarySearchTree is Empty");
}
Node curr=root;
while (curr.right!=null){
curr=curr.right;
}
return curr.e;
}
/**
* 删除最大节点
* @return
*/
public E removeMaximum(){
E max=maximum();
root=removeMaximum(root);
return max;
}
/**
* 递归删除最大节点
* @param node
* @return
*/
private Node removeMaximum(Node node){
if(node.right==null){
Node leftNode = node.left;
size--;
node.left=null;
return leftNode;
}
node.right=removeMaximum(node.right);
return node;
}
/**
* 删除值为e的节点
* @param e
*/
public void remove(E e){
if (size == 0) {
throw new IllegalArgumentException("BinarySearchTree is Empty");
}
remove(root,e);
}
/**
* 删除任一节点
* 分为三种情况:
* 1.该节点没有左子树,则用其右子树替代该节点
* 2.该节点没有右子树,则用其左子树替代该节点
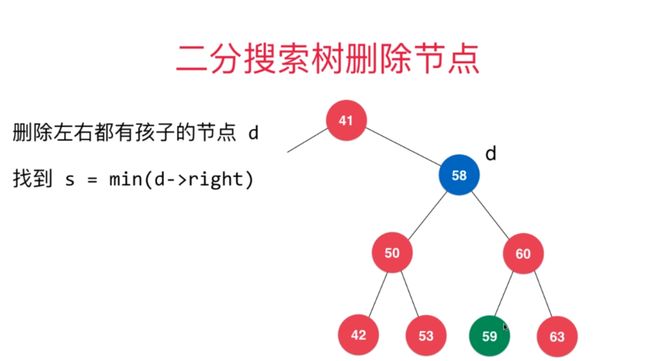
* 3.该节点既有左子树,又有右子树,可以用其左子树的最大节点替代该节点,并删除左子树最大节点(也就是该节点的前驱),
* 也可以用右子树的最小节点替代该节点,并删除右子树最小节点(也就是该节点的后继)
*这里使用了后继做给替换节点的方法
* @param node
* @param e
* @return
*/
private Node remove(Node node,E e){
if(node==null){
return null;
}
if(node.e.compareTo(e)==0){
if(node.left==null){//如果没有左子树,则直接将右子树作为根节点
Node right = node.right;
node.right=null;
size--;
return right;
} else if(node.right==null){//如果没有右子树,则直接将左子树作为根节点
Node left = node.left;
node.left=null;
size--;
return left;
}else{//如果左右子树都有,则将右子树的最小节点作为作为替代,并删除右子树的最小节点
Node minimum = minimum(node.right);
Node rightMinNode = removeMinimum(node.right);//做了size--
node.e=minimum.e;
node.right=rightMinNode;
return node;
}
} else if(node.e.compareTo(e)<=0){
node.right=remove(node.right,e);
}else {
node.left=remove(node.left,e);
}
return node;
}
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
generateBinarySearchTreeString(root, 0, builder);
return builder.toString();
}
private void generateBinarySearchTreeString(Node node, int depth, StringBuilder res) {
if (node == null) {
res.append(generateBinarySearchTreeDepthString(depth) + "null\n");
return;
}
res.append(generateBinarySearchTreeDepthString(depth) + node.e + "\n");
generateBinarySearchTreeString(node.left, depth + 1, res);
generateBinarySearchTreeString(node.right, depth + 1, res);
}
private String generateBinarySearchTreeDepthString(int depth) {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < depth; i++) {
builder.append("--");
}
return builder.toString();
}
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
int[] arr = {5, 6, 2, 3, 46, 14, 48, 1, 7,47,50};
for (int i : arr) {
tree.add(i);
}
/* 5
/ \
2 6
/ \ \
1 3 46
/ \
14 48
/
7
*/
// System.out.println(tree.contains(8));
// System.out.println(tree.toString());
// tree.preOrder();
// System.out.println();
// tree.preOrderNR();
// tree.extentOrder();
// Integer minimum = tree.minimum();
// Integer minimum = tree.minimumNR();
// System.out.println("minimum:" + minimum);
// Integer maximum = tree.maximum();
// Integer maximum = tree.maximumNR();
// System.out.println("maximum: "+maximum);
// System.out.println("remove minimum:"+tree.removeMinimum());
// tree.preOrder();
// System.out.println();
// System.out.println("remove maximum:"+tree.removeMaximum());
// tree.preOrder();
// tree.inOrder();
// tree.postOrder();
tree.preOrder();
System.out.println();
tree.remove(46);
tree.preOrder();
}
}
-
使用后继作为替换元素删除任一节点(右子树最小值)
-
也可以使用前驱作为替换元素删除任一节点(左子树最大值)