克鲁斯卡尔Kruskal 算法最小生成树

简介

Kruskal算法是一种用来查找最小生成树的算法，由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪心算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

应用场景

1. 公交站牌问题
2. 修路问题

概念

先构造一个只含 n 个顶点、而边集为空的子图，把子图中各个顶点看成各棵树上的根结点，之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，即把两棵树合成一棵树，反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直到森林中只有一棵树，也即子图中含有 n-1 条边为止。 [1]

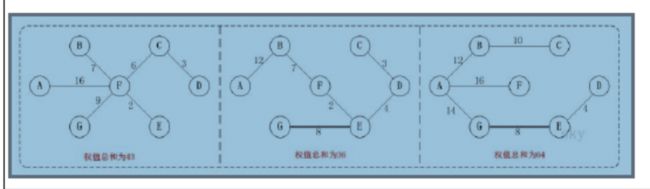
图解步骤

1. 先对数据进行排序
2. 将权值最小的放入结果集
3. 依次处理
4. 最重要的是不要出现闭环

避免闭环的解决思路

1. 记录顶点在最小生成树的终点（终点一定最小生成树最大的顶点）
2. 每次需要将一条边加入到最小生成树时，判断该边与两个顶点是否有重合
3. 如果有重合，则构成回路

代码实现

class Kruskal {

    /**
     * 边的个数
     *
     * @var integer
     */
    private $edgeNum = 0;

    /**
     * 顶点的数组
     *
     * @var array
     */
    private $vertexs = [];

    /**
     * 邻接矩阵
     *
     * @var array
     */
    private $matrix = [];    

    public static function factory(){
        //           0    1    2    3    4    5    6
        $vertexs = ["A", "B", "C", "D", "E", "F", "G"];
        $matrix = [
            //A   B   C   D   E   F    G
            [0,  12, -1, -1, -1, 16,  14], // A
            [12,  0, 10, -1, -1,  7,  -1], // B
            [-1, 10,  0,  3,  5,  6,  -1], // C
            [-1, -1,  3,  0,  4, -1,  -1], // D
            [-1, -1,  5,  4,  0,  2,   8], // E
            [16,  7,  6, -1,  2,  0,   9], // F
            [14, -1, -1, -1,  8,  9,   0]  // G
        ];

        $rs = new Kruskal($vertexs, $matrix);
    }

    public function __construct($vertexs, $matrix) {
        $vlen = count($vertexs);
        $this->vertexs = $vertexs;
        $this->matrix = $matrix;

        // 统计边的条数
        for ($i=0; $i<$vlen; $i++) {
            for($j=$i+1; $j<$vlen; $j++) {
                if ($this->matrix[$i][$j] != -1) {
                    $this->edgeNum++;
                }
            }
        }

        $this->kruskal1();
    }

    public function kruskal1() {
        $index = 0;
        $ends = array_fill(0, $this->edgeNum, 0);

        $rets = [];
        $edges = $this->getEdges();

        $sort = [];
        foreach($edges as $val) {
            $sort[] = $val->weight;
        }
        array_multisort($sort, SORT_ASC, $edges);


        for($i=0; $i<$this->edgeNum; $i++) {

            $p1 = $this->getPosition($edges[$i]->start);
            $p2 = $this->getPosition($edges[$i]->end);

            $m = $this->getEnd($ends, $p1);
            $n = $this->getEnd($ends, $p2);

            if ($m != $n) {
                $ends[$m] = $n;
                $rets[$index++] = $edges[$i];
            }
        }

        foreach($rets as $val) {
            echo sprintf("%s->%s=%s ", $val->start, $val->end, $val->weight);
        }

        echo "\n";
    }

    public function getEdges() {
        $index = 0;
        $edges = [];
        for($i = 0; $i < count($this->vertexs); $i++) {
            for($j=$i+1; $j < count($this->vertexs); $j++) {
                if($this->matrix[$i][$j] != -1) {
                    $edges[$index++] = new edata($this->vertexs[$i], $this->vertexs[$j], $this->matrix[$i][$j]);
                }
            }
        }
        return $edges;
    }

    public function getPosition($ch) {

        for($i=0; $ivertexs); $i++) {
            if ($ch == $this->vertexs[$i]) {
                return $i;
            }
        }
        return -1;
    }

    public function getEnd($ends, $i) {
        while($ends[$i] != 0) {
            $i = $ends[$i];
        }
        return $i;
    }
}

class edata {

    public $start;
    public $end;
    public $weight;

    public function __construct($start, $end, $weight) {
        $this->start = $start;
        $this->end = $end;
        $this->weight = $weight;
    }

    public function toString() {
        return "EData [<" + $this->start + ", " + $this->end + ">= " + $this->weight + "]";
    }

}

$rs = Kruskal::factory();

运行结果

E->F=2 C->D=3 D->E=4 B->F=7 E->G=8 A->B=12