二叉树原理及编程详解(二)红黑树|二叉搜索树
目录
一、红黑树
1.1 定义
1.2 性质
1.3 基本操作
左旋
右旋
变色
1.4 操作
查找
插入
直接插入
插入后需要变形与递归
1.5 一个插入实例
二、二叉搜索树
2.1 定义与性质
2.2 判断二叉搜索树
三、两道编程题及思路
3.1 是排序二叉树
3.2 带有指向父节点的指针
3.3 没有父指针
一、红黑树
1.1 定义
https://baike.baidu.com/item/%E7%BA%A2%E9%BB%91%E6%A0%91/2413209?fr=aladdin
红黑树(Red Black Tree) 是一种自平衡二叉查找树,典型的用途是实现关联数组。它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。
1.2 性质
https://www.jianshu.com/p/e136ec79235c
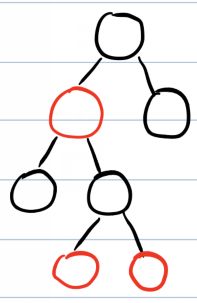
一层红,一层黑。也叫二叉查找树
- 性质1:每个节点要么是黑色,要么是红色。
- 性质2:根节点是黑色。
- 性质3:每个叶子节点(NIL)是黑色。(根与叶子必是黑色)
- 性质4:每个红色结点的两个子结点一定都是黑色。
- 性质5:任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
红黑树并不是一个完美平衡二叉查找树,例如上面,左子树比右子树高2,但是根据性质5,性质5:任意一结点到每个叶子结点的路径都包含数量相同的黑结点。所以我们叫红黑树这种平衡为黑色完美平衡。
1.3 基本操作
排序二叉树左旋或者右旋操作之后,依然是排序二叉树?是的。
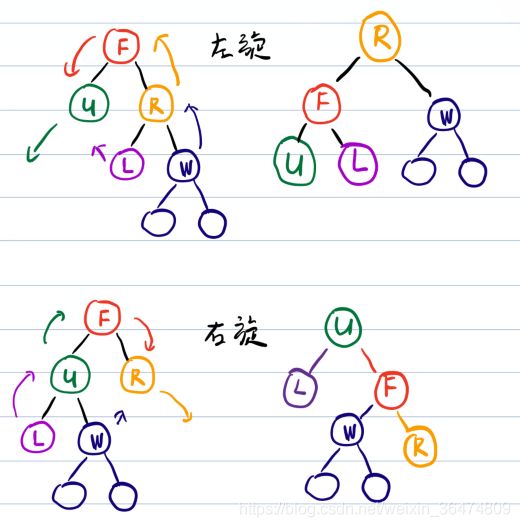
左旋
- 以某节点作为支点F
- F的右节点R变为支点的父节点
- 右子结点R的左子结点L变为旋转结点的右子结点
- 左子结点保持不变
右旋
- 以某个结点作为支点(旋转结点),
- 其左子结点变为旋转结点的父结点,
- 左子结点的右子结点变为旋转结点的左子结点,
- 右子结点保持不变。
左旋只影响旋转结点和其右子树的结构,把右子树的结点往左子树挪了。
右旋只影响旋转结点和其左子树的结构,把左子树的结点往右子树挪了。
变色
结点的颜色由红变黑或由黑变红。
1.4 操作
查找
因为红黑树是一颗二叉平衡树,并且查找不会破坏树的平衡,所以查找跟二叉平衡树的查找无异:
- 从根结点开始查找,把根结点设置为当前结点;
- 若当前结点为空,返回null;
- 若当前结点不为空,用当前结点的key跟查找key作比较;
- 若当前结点key等于查找key,那么该key就是查找目标,返回当前结点;
- 若当前结点key大于查找key,把当前结点的左子结点设置为当前结点,重复步骤2;
- 若当前结点key小于查找key,把当前结点的右子结点设置为当前结点,重复步骤2;
插入
直接插入
两步。1.查找插入位置。2.插入后的自平衡。
直接插入的情况:
- 空树:直接插入(不需自平衡)。
- 插入节点值已经存在:且插入节点父节点为黑色:直接插入(不需自平衡)。
插入后需要变形与递归
存在下面两种基本情况,此后的情况可根据下面两种进行变形。
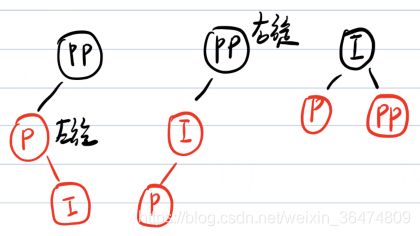
1. 插入节点父节点的父节点为红色,叔节点存在且为红色:
红黑树自底向上进行生长,所以插入节点为红,自底向上到祖父节点依次进行变色。(最复杂的情况,增加了路径中黑色节点的数目)
此时,相当于插入了祖父节点PP,往下递归。
2. 插入节点叔节点不存在:插入,自底向上父节点、祖父节点进行旋转操作(即可完成平衡,相对简单)。
详见:
https://www.jianshu.com/p/e136ec79235c
1.5 一个插入实例
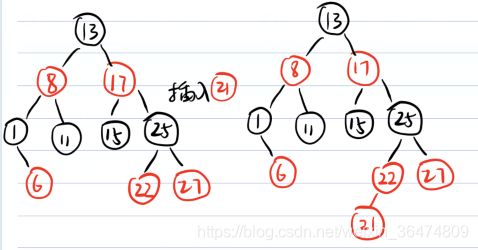
步骤1:需要插入21,相当于红色子节点的左子树。(叔节点存在且为红色)
步骤2:变色,插入之后,不能满足红色节点不能相邻,所以插入节点的父节点与祖父节点变色。
步骤3:变色后相当于在祖父位置插入节点25,节点25的叔节点存在且红节点,需要向上变色。
步骤4:变色后,根节点为红色,需要左旋转操作把根节点换位黑色。
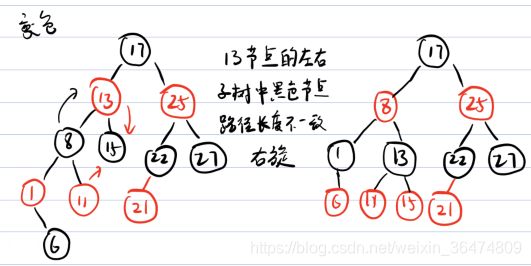
步骤5, 因为不满足一层红色一层黑色,向下递归一个节点右旋。
二、二叉搜索树
2.1 定义与性质
https://blog.csdn.net/hh66__66hh/article/details/82947113
二叉查找树(Binary Search Tree),也叫二叉排序树。
- 左子树节点均小于根节点,
- 右子树节点均大于根节点,
- 左右子树也构成儿叉搜索树。
最小值与最大值
查找最小值:因为二叉搜索树中,左节点比父节点小,故最小值肯定在树的左下角。从根节点开始,判断它的左节点存不存在。如果存在,继续找这个左节点的左节点,如此类推,直到找到某个节点的左节点不存在时,此节点就是最小值。
查找最大值:因为二叉搜索树中,右节点比父节点大,故最大值肯定在树的右下角。从根节点开始,判断它的右节点存不存在。如果存在,继续找这个右节点的右节点,如此类推,直到找到某个节点的右节点不存在时,此节点就是最大值。
2.2 判断二叉搜索树
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
class Solution {
public:
bool VerifySquenceOfBST(vector sequence) {
int vector_size = sequence.size();
if (vector_size < 1)return false;
int root = sequence[vector_size - 1];
int location = 0;
vector left_sequence, right_sequence;
while (sequence[location] < root){
left_sequence.push_back(sequence[location]);
location++;
}
while ((sequence[location] > root)){
right_sequence.push_back(sequence[location]);
location++;
}
if (location < vector_size - 1)
return false;
else{
bool left = true;
if (left_sequence.size()>1)left = VerifySquenceOfBST(left_sequence);
bool right = true;
if (right_sequence.size()>1)right = VerifySquenceOfBST(right_sequence);
return left&&right;
}
}
};
三、两道编程题及思路
剑指offer后面P345
题干:已经知道两个节点,如何求他们的公共祖先?
3.1 是排序二叉树
从根向下遍历,如果值介于两个节点值之间,则这个结点必然是两个值的公共祖先。
3.2 带有指向父节点的指针
则相当于判断两个链表的第一个公共节点的问题。
3.3 没有父指针
如果没有父指针:
找到根节点到通过的节点回归一个链表,然后找到两个链表的公共节点。
这个问题就转换成了两个问题:
- 如何从根节点找到到一个节点的路径?
- 如何找链表的最后公共节点?