流形学习(Manifold Learning)

流形学习(Manifold Learning)

流形学习是非线性降维的重要研究领域，

前言

PCA是目前应用最广泛的线性降维方法，采用线性投影的方法进行数据降维，使数据在给定方向上的投影得到最大的投影方差，当流形是一个线性流形时，PCA得到的结果是最优的，PCA无法有效处理非线性流形上的数据。

流行学习简介

流形： 流形(manifold)是一般几何对象的总称，包括各种维度的曲线与曲面等，和一般的降维分析一样，流形学习是把一组在高维空间中的数据在低维空间中重新表示。不同之处是，在流形学习中假设：所处理的数据采样与一个潜在的流形上，或者说对于这组数据存在一个潜在的流形。

流形上的点本身是没有坐标的，所以为了表示这些数据点，我们把流形放入到外围空间(ambient space)，用外围空间上的坐标来表示流形上的点，例如三维空间 R^3 中球面是一个2维曲面，即球面上只有两个自由度，但我们一般采用外围空间R^3 空间中的坐标来表示这个球面。

流行学习可以概括为：在保持流形上点的某些几何性质特征的情况下，找出一组对应的内蕴坐标(intrinsic coordinate)，将流形尽量好的展开在低维平面上，这种低维表示也叫内蕴特征(intrinsic feature)，外围空间的维数叫观察维数，其表示叫自然坐标，在统计上称为observation。

流形学习 = 微分流形 + 黎曼几何

主要的代表方法

1) Isomap (等距映射)

Isomap = MDS(Multidimensional Scaling)多维尺度变换 + 测地线距离

MDS： MDS是理论上保持欧式距离的一种经典方法，MDS最早用来做数据的可视化，MDS得到的低维表示中心在原地，所以又可以说是保持内积大小，MDS降维后的任意两点的距离（内积）与高维空间的距离相等或近似相等。

因此MDS在流形数据处理上，保持欧式距离不变的理论不可行（失效），Isomap就是改进的MDS方法，在流形非线性降维领域的应用方法。

Isomap的理论框架为MDS，放在流形的理论框架中，原始的高维空间欧氏距离换成了流形上的测地线距离。Isomap是把任意两点的测地距离(准确地说是最短距离)作为流形的几何描述，用MDS理论框架保持点与点之间的最短距离。

测地线的计算：在流形结构未知，数据采样有限的情况下， 通过构造数据点间的邻接图(Graph)，用图上的最短距离来近似测地线距离，当数据点趋于无穷多时，这个估计近似距离趋向于真实的测地线距离。

此算法是计算机系中常用的图论经典算法。

Isomap算法步骤：

1.构建近邻图G。如果样本点 i 和样本点 j 之间的距离小于设定的距离阈值（由于距离阈值较小，可用欧氏距离近似），或它们为K近邻，则连接样本点 i 与样本点 j ，为相邻点。

2.计算样本点两两之间的测地距离，邻近点的测地距离用欧氏距离近似表示，较远两点间的测地距离用图上两点间的最短距离近似表示（如下图红线表示最短距离，蓝线表示测地距离），建立测地距离矩阵 DG=dG(xi,xj) D G = d G ( x i , x j )

3.利用MDS算法构造内在d维子空间，最小化下式： E=∥τ(DG)−τ(DY)∥L2 E = ‖ τ ( D G ) − τ ( D Y ) ‖ L 2

矩阵变换算子 τ(D)=−HSH/2 τ ( D ) = − H S H / 2 将距离转换成MDS所需的内积形式，其中S是平方距离矩阵， Sxi,xj=D2xi,xj S x i , x j = D x i , x j 2 是集中矩阵， Hxi,xj=δxi,xj−1/N H x i , x j = δ x i , x j − 1 / N ，上式的最小值可以通过求解矩阵 τ(DG) τ ( D G ) 的d个最大特征值对应的特征向量来实现。

2) LLE(Locally Linear Embedding) 局部线性嵌入

LLE基本思想：

一个流形在很小的局部邻域上可以近似看成是欧氏的，即局部线性的。那么，在小的局部邻域中，一个点就可以用它周围的点在最小二乘意义下的最优线性来表示。LLE方法即是把这种线性拟合的系数当成这个流形的局部几何性质的描述。同样的，一个后的低维空间数据表示，也就应该具有同样的局部几何性质，所以利用同样的线性表示的表达式，最终写成一个二次型的形式 。

概括的来说就是：”流形在局部可以近似等价于欧氏空间“。

LLE算法步骤：

1.构建邻域图。对于原始空间中任一给定的样本点 xi x i ，用K近邻法得到它的一组邻域点 xj x j ；

2.计算权重。由局部线性假设，样本点 xi x i 可用K 个邻域点 xj x j 线性表示出来，即 xi≈∑Wi,jxj x i ≈ ∑ W i , j x j ，用权重描述出每一样本点与其邻域点之间的关系，权重 Wi,j W i , j 是使得样本点 xi x i 用其K个邻域点 xj x j 重构误差最小的解的系数：

ξ(W)=∑i|xi−∑jWi,jxj|2 ξ ( W ) = ∑ i | x i − ∑ j W i , j x j | 2

使 ξ(W) ξ ( W ) 的值为最小，则 Wi,j W i , j 即为各样本点最优的线性表示参数，即权重。

3.将这种局部线性结构嵌入低维空间。嵌入操作是通过最小化误差来尽可能多的保留原空间的性质：
ξ(y)=∑i|yi−∑jWi,jyj|2 ξ ( y ) = ∑ i | y i − ∑ j W i , j y j | 2
这里的 Wi,j W i , j 是第二步计算的权重值， yi y i 与 yj y j 是样本点在嵌入空间的投影。

Isomap 与LLE的比较：

1. Isomap与LLE从不同的角度出发来实现同一个目标，它们都能从某种程度上发现并在映射的过程中保持流形的几何特征。
2. Isomap希望保持任意两点间的测地线距离；LLE希望保持局部线性关系。
3. 从保持几何角度来看，Isomap保留了更多信息，然而Isomap方法的一个问题是要考虑任意两点之间的关系，这个数量随着数据点的增多而呈现爆炸性增长，从而增加计算负荷，在大数据时代，使用全局方法分析巨型数据结构正在变得越来越困难。
4. 因此，以LLE为开端的局部分析方法的变种和相关理论正在受到越来越多的关注。

3) LE (Laplacian Eigenmaps) 拉普拉斯特征映射

谱图理论：

拉普拉斯矩阵也叫导纳矩阵，基尔霍夫矩阵或离散拉普拉斯算子。主要应用在图论中，作为一个图的矩阵表示。

给定一个有n个顶点的图G，它的拉普拉斯矩阵定义为： L=(li,j)n×n L = ( l i , j ) n × n ， 定义为 L=D−W L = D − W ，

其中D 为图的度矩阵，是对角线元素为度数的对角阵； W为图的邻接矩阵，也叫权重矩阵，

如下例子所示：

度矩阵D ，在无向图中，对角线为每个元素的度数

邻接矩阵W，若俩顶点相连，则对应的元素为1 ，乘以权重 wi,j w i , j 即为权重函数

拉普拉斯矩阵L = D-W ，

对拉普拉斯矩阵 L=(li,j)n×n L = ( l i , j ) n × n ，

当 i=j i = j 时， li,j=deg(vi) l i , j = d e g ( v i ) ， deg(vi)为 d e g ( v i ) 为 顶点v_i 的度数；

当 i≠j i ≠ j 时，但顶点 vi v i 与顶点 vj v j 相连，则 li,j=−1 l i , j = − 1 ；

其他情况， li,j=0 l i , j = 0 ；

拉普拉斯矩阵为对称矩阵，每行或每列元素和为0 。

拉普拉斯矩阵的特征向量成了一组正交向量积，被大量用于学习问题。

LE基本思想：

使用一个无向有权图来描述一个流形，通过图的嵌入(graph embedding) 来找低维表示。其实就是保持图的局部邻接关系的前提下，把流形数据形成的图从高位空间映射在一个低维空间中。

LE希望保持流形中的近邻关系：将原始空间中相近的点映射成目标空间中相近的点。

主要思想的数学表达： 令样本集 X=(x1,x2...xn) X = ( x 1 , x 2 . . . x n ) ，投影后的样本集为 Y=(y1,y2...yn) Y = ( y 1 , y 2 . . . y n )

LE的目标是最小化目标函数： E(y)=∑ni,j(yi−yj)2Wi,j E ( y ) = ∑ i , j n ( y i − y j ) 2 W i , j ，为了使最小化问题解唯一，必须加上尺度归一化的限制条件，所以目标函数变为： argminyTDy=1yTLy a r g m i n y T D y = 1 y T L y

约束条件： yTDy=1 y T D y = 1 ，去除任意的缩放，即标准化为1

转化成一个特征向量问题：L y = \lambda D y

LE求特征向量的问题对应于连续的时候求拉普拉斯特征函数的问题，

LE算法步骤：

1. 构建近邻图
2. 计算每条边的权重，（不相连的边权重为0）： 热核权重： wi,j=exp(∥xi−xj∥2σ2) w i , j = e x p ( ‖ x i − x j ‖ 2 σ 2 ) ，将权重 wi,j w i , j 代入到拉普拉斯矩阵中得到拉式矩阵L ，
   （权重 wi,j w i , j 计算的另一种方法，节点相邻取为1，不相邻取为 0）
3. 求解特征向量方程： Ly=λDy L y = λ D y ，将点 xi x i 映射到 yi(y1(i),y2(i)...yd(i)) y i ( y 1 ( i ) , y 2 ( i ) . . . y d ( i ) ) ，

4) LPP (Locality Preserving Projection) 局部保留投影

LPP算法提出的目的是为了实现非线性流形的学习和分析，LPP可以提取最具有判别性的特征来进行降维，是一种保留了局部信息，降低影响图像识别的诸多因素的降维方法，这种算法本质上是一种线性降维方法，由于其巧妙的结合了拉普拉斯特征映射算法（LE）的思想，从而可以在对高维数据进行降维后有效地保留数据内部的非线性结构。

与其他非线性降维方法相比，LPP方法可以将新增的测试数据点，通过映射在降维后的子空间找到对应的位置，而其他非线性方法只能定义训练数据点，无法评估新的测试数据。LPP方法可以很容易地将新的测试数据点根据特征映射关系（矩阵），投影映射在低维空间中。

将 n 维原数据映射为 l 维数据，l<< n ；实现数据降维，样本个数为m ；

LPP算法步骤：

1.构建邻接图，可以得到度矩阵D ，邻接矩阵W ，以及拉普拉斯矩阵 L = D-W ；

2.计算每条边的权重，（不相连的边权重为0）： 热核权重： wi,j=exp(∥xi−xj∥2σ2) w i , j = e x p ( ‖ x i − x j ‖ 2 σ 2 ) ，将权重 wi,j w i , j 代入到拉普拉斯矩阵中得到拉式矩阵L ，

（简单权重 wi,j w i , j 计算方法：节点相邻取为1，不相邻取为 0）

3.求解特征向量方程： XLXTa=λXDXTa X L X T a = λ X D X T a ，即 ((XDXT)−1XLXT)a=λa ( ( X D X T ) − 1 X L X T ) a = λ a ；将解得的特征值 λ λ 按照从小到大的顺序排列，共有 n 个特征值，取其最小的 l l 个特征值， λ1<λ2<...<λl λ 1 < λ 2 < . . . < λ l ，对应的 l l 个特征向量组成的向量为矩阵 A=(a1,a2,...al) A = ( a 1 , a 2 , . . . a l ) ，

xi−>yi x i − > y i 的映射为： yi=ATxi,A=(a1,a2,...al) y i = A T x i , A = ( a 1 , a 2 , . . . a l )
A∈Rn×l A ∈ R n × l ；

xi∈Rn×1 x i ∈ R n × 1 ， AT∈Rl×n A T ∈ R l × n ， yi∈Rl×1 y i ∈ R l × 1 ，

推导过程：

Y Y 矩阵规格为 l×m l × m ；求得最佳的投影，将矩阵 Y Y 按行分为 l l 个行向量 yTi=gTi=(y1,y2,....ym) y i T = g i T = ( y 1 , y 2 , . . . . y m ) ；即 gTi g i T 有m个元素， gTi g i T 的规格为 1×m ；则根据投影关系可知， gTi=yT=aTX g i T = y T = a T X ；

也可以这样认为：当只有一个特征向量时，一个样本数据投影为一个一维空间上的点，原始数据矩阵投影为： yT=aTX y T = a T X ， yT y T 的规格为 1×m 1 × m ；

将原始矩阵 X 按列分为m个列向量 xi x i ，即为每个样本数据，则限制函数是外围欧氏空间的线性函数： f(xi)=yi=aTxi f ( x i ) = y i = a T x i ， a∈Rn×1 a ∈ R n × 1 为 A 中的一个特征向量； xi∈Rn×1 x i ∈ R n × 1 为一个原始样本数据 ； yi y i 为 gTi g i T 即 yT y T 的一个元素， 即为矩阵 Y Y 中的一个元素；

最小化目标函数 ∑i,j∥yi−yj∥2Wi,j ∑ i , j ‖ y i − y j ‖ 2 W i , j ； Wi,j W i , j 为一个数值，整个目标函数的值为一个数， yi=aTxi y i = a T x i ；

目标函数 f(x) 就是用设计变量来表示的所追求的目标形式，所以目标函数就是设计变量的函数，是一个标量，建立目标函数的过程就是寻找设计变量与目标的关系的过程，从工程意义讲，目标函数是系统的性能最优标准，

12∑i,j∥yi−yj∥2Wi,j=12∑i,j∥aTxi−aTxj∥2Wi,j=∑iaTxiDi,ixTia−∑i,jaTxiWi,jxTja=aTX(D−W)XTa=aTXLXTa 1 2 ∑ i , j ‖ y i − y j ‖ 2 W i , j = 1 2 ∑ i , j ‖ a T x i − a T x j ‖ 2 W i , j = ∑ i a T x i D i , i x i T a − ∑ i , j a T x i W i , j x j T a = a T X ( D − W ) X T a = a T X L X T a

Di,i=∑jWi,j D i , i = ∑ j W i , j ， L=D−W L = D − W

加上尺度归一限制： yTDy=1 y T D y = 1 ，得到 aTXDXTa=1 a T X D X T a = 1

即求在 aTXDXTa=1 a T X D X T a = 1 的条件下，使得 aTXLXTa a T X L X T a 的值最小。

即 arg minaTXDXaaTXLXTa m i n a T X D X a a T X L X T a

最终转化为求解如下广义特征向量问题： XLXTa=λXDXTa￥，其中 X L X T a = λ X D X T a ￥ ， 其 中 X = (x_1, x_2…x_n)$ 为数据矩阵。

等式两边同时左乘 (XDXT)−1 ( X D X T ) − 1 ，得到 (XDXT)−1XLXTa=λa ( X D X T ) − 1 X L X T a = λ a ，

且 XLXT X L X T 和 XDXT X D X T 是对称的半正定的，因此最小化目标函数转换为求解广义特征值问题。将特征值按从大到小的顺序排列，取最大的 l l 个特征值，即求矩阵 (XDXT)−1XLXT ( X D X T ) − 1 X L X T 的最大的 l l 个特征值 λ λ ， 和特征向量 a a 及其所张成的映射矩阵 S S ，（广义瑞利商）

其中 L 为拉普拉斯矩阵 L=D−W L = D − W ； D 为度矩阵（对角阵）；W 为邻接矩阵，也叫权重矩阵。

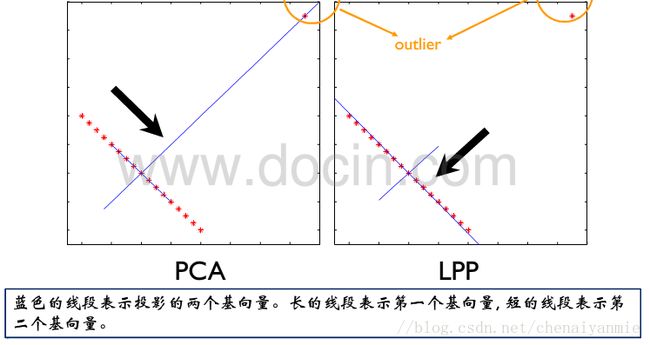
LPP与PCA、LDA比较：

PCA考虑的是全局信息，LPP是第一个考虑流形结构的线性方法。PCA对异常点或噪声点很敏感，分辨能力较弱，因此容易受到异常点对投影映射结果的影响，而LPP方法对异常点不敏感，因此受其干扰较小，具有较强的分辨力。

LPP与LDA方法有一些相似之处，也有许多不同之处，LPP是无监督的学习方法，LDA方法是基于监督的学习方法。LDA是为了是类间方差与类内方差的比值最大，从而达到“相同类的点紧密，不同类的点分散”的分类效果；LPP是为了使高维数据点间的距离远近关系在降维后，对应映射点的距离关系保持不变，即“高维空间点之间距离近的点，在低维空间映射点间的距离也很近”，即保持了高维流形数据的一种拓扑结构不变。