2018清北学堂普及组冲刺班6连考总结反思
DAY 1
Problem 1 A(A.cpp/c/pas)
【题目描述】
给出一个n*m的网格,其中小明初始站在(x,y)这个位置,网格内无障碍,小明可以向上下左右四个方向一步走一格,问小明最少走几步可以走出网格。
【输入格式】
输入文件A .in
第一行四个整数n,m,x,y。
【输出格式】
输出文件A.out
一行一个整数表示答案。
【样例输入】
3 3 2 2
【样例输出】
2
【数据范围】
对于 30% 数据 n,m<=3
对于 50% 数据 n,m<=1000
对于 100% 数据 n,m<=1000000000,1<=x<=n,1<=y<=m;
想法:很简单的一道题目,但是我想多了,广搜也会超时呀!!!
源代码
#include
using namespace std;
int dx[5]={0,0,-1,0,1};
int dy[5]={0,-1,0,1,0};
struct node
{
long x;
long y;
long ans;
}p,q;
long start_x,start_y,n,m;
int main()
{
freopen("A.in","r",stdin);
freopen("A.out","w",stdout);
cin>>n>>m>>start_x>>start_y;
if (start_x < 1 || start_y < 1 || start_x > n || start_y > m)
{
cout<<0;
return 0;
}
queue line;
p.x = start_x;
p.y = start_y;
p.ans = 0;
line.push(p);
while (!line.empty())
{
p = line.front();
// if (p.x == n && p.y == m)
// {
// cout< n || yy < 1 || yy > m)
{
cout< 我还是搜索写上头了QAQ
std:
#include
using namespace std;
int n,m,x,y,ans1,ans2;
int main()
{
cin>>n>>m>>x>>y;
//我也想到直接判断直线距离了呀 哎。。。可惜
ans1 = min(x,abs(x-n));
ans2 = min(y,abs(y-m));
cout< 反思:要注意审题,对合适的题型使用合适的算法,不要再犯这样坑爹的低级错误了
Problem 2 B(B.cpp/c/pas)
【题目描述】
Lucy家门前的大街上有n家店,lucy是一个喜欢收藏机械键盘的女孩子,这n家店中第i家店卖的键盘价格为V[i],lucy前前后后有q天心血来潮买电脑,其中第i次买电脑的预算是K[i],问每一次有多少店的键盘能供lucy选择,能选择当且仅当该店的键盘价格小于等于lucy的预算。
【输入格式】
输入文件B.in。
输入文件第一行两个整数n,q。
接下来一行n个整数,其中第i个整数为V[i]。
第q行每行一个整数K代表该次买电脑的预算。
【输出格式】
输出文件B.out。
输出文件q行,第i行表示第i次买电脑,能有多少家店可供选择。
【样例输入】
6 3
6 5 4 3 2 1
1
3
5
【样例输出】
1
3
5
【数据范围】
对于30%的数据,n,q<=1000。
对于另外30%的数据,n,q<=100000,0<=V[i],K[i]<=100000
对于100%的数据,
n<=100000,m<=100000,0<=V[i],K[i]<=10^9。
想法:自己上来就写了,没看清数据范围QAQ(看清了也写不来 ) 这题是二分呀!!!
源代码
#include
using namespace std;
long a[100009],n,q,k,b[100009];
long total;
int main()
{
freopen("B.in","r",stdin);
freopen("B.out","w",stdout);
cin>>n>>q;
if (n == 0)
{
for (int i = 1; i <= q; i++)
cout<<0<>a[i];
sort(a+1,a+n+1);
for (int i = 1; i <= q; i++)
cin>>b[i];
for (int i = 1; i <= q; i++)
{
total = 0;
for (int j = 1; j <= n; j++)
if (b[i] >= a[j]) total++;
else
break;
cout< std:
#include
using namespace std;
int n,q,k;
int a[100009];
int main()
{
cin>>n>>q;
for (int i = 1; i <= n; i++)
cin>>a[i];
sort(a+1,a+n+1);
for (int i = 1; i <= q; i++)
{
cin>>k;
int p = upper_bound(a+1,a+n+1,k)-a; //二分函数,找到大于的返回
cout< 反思:要注意看范围 要注意看范围 要注意看范围(重要的事情说3遍 ),要加强对二分的练习
Problem 3 C(C.cpp/c/pas)
【题目描述】
有一个无限范围的蜂窝状的网格,小明决定在这个网格中探险。
我们看一下这一张图,来看整个网格的坐标结构。

小明从(0,0)点出发,按照旋涡状移动(见下图),求移动n步后,小明所处的坐标。
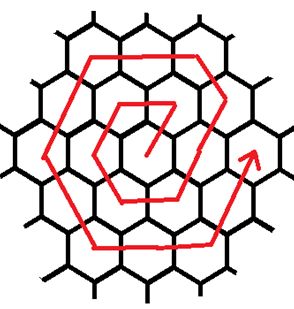
【输入格式】
输入文件C.in
输入一行一个整数n。
【输出格式】
输出文件C.out
输出一行两个整数x,y表示小明n步之后所处的坐标。
【样例输入1】
3
【样例输出1】
-2 0
【样例输入2】
7
【样例输出2】
3 2
【数据范围】
对于30%的数据,n<=30;
对于50%的数据,n<=500;
对于100%的数据,n<=10^18;
std:
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int up=577350270;
ll n,rest,x,y;
int main()
{
freopen("C.in","r",stdin);
freopen("C.out","w",stdout);
scanf("%I64d",&n);
if (n==0) {printf("0 0");return 0;}
int l=1,r=up,mid,ans;
while (l<=r)
{
mid=(l+r)>>1;
if (3ll*mid*(mid+1)>=n) ans=mid,r=mid-1;else l=mid+1;
}
rest=n-3ll*ans*(ans-1);rest--;
x=ans*2-1,y=2;
if (rest 2018.10.1
DAY 2
Problem 1 A(A.cpp/c/pas)
【题目描述】
初始有n个包子,第i个包子的大小为a[i],我们要把所有包子放在蒸笼里蒸熟。由于强迫症的原因,对于每一笼包子,包子的大小必须是相同的,在这个问题中我们假设一个蒸笼是无限大的,也就是可以放任意多个包子。
我们现在想知道,如何把给包子安排对应的蒸笼,使得蒸笼的数量最少。输出最少的蒸笼的数量,以及含包子最多的蒸笼的包子数量是多少。
【输入格式】
输入文件A.in。
第一行一个整数n。
第二行n个整数,其中第i个整数a[i]表示第i个包子的大小。
【输出格式】
输出文件A.out
一行两个整数分别表示最优方案下,包子最多的蒸笼的包子数量和最少蒸笼数量。
【样例输入1】
3
1 2 3
【样例输出1】
1 3
【样例输入2】
4
6 5 6 7
【样例输出2】
2 3
【数据范围】
对于 30% 数据 n,a[i]<=1000
对于 50% 数据 n<=100000,a[i]<=1000
对于 100% 数据 n,m<=100000,a[i]<=10^9
想法:长了上一次的教训,这次乖乖的写线性的算法了(拜拜二重for,拿走拿走不客气 ),觉得可以用队列的维护来写
源代码:
#include
using namespace std;
long a[100009],i,k,sum,total,n;
int main()
{
freopen("A.in","r",stdin);
freopen("A.out","w",stdout);
queue line;
cin>>n;
for (i = 1; i <= n; i++)
cin>>a[i];
sort(a+1,a+n+1);
i = 1;
k = 1;
sum = 1;
total = 1;
line.push(a[i]);
while (i < n) //维护队列,线性算法
{
i++;
if (a[i] != line.front())
{
total = max(total,sum);
k++;
line.pop();
line.push(a[i]);
sum = 1;
}
else
sum++;
}
total = max(total,sum);
cout< std:
#include
#include
#include 反思:多多注意对时间复杂度的减少,尽力写最优的算法
Problem 2 B(B.cpp/c/pas)
【题目描述】
定义n!为123……*n。
我们求现在要求(0!+1!+2!……+n!)对m取模的结果。
(提示:数学上定义0!为1。)
【输入格式】
输入文件B.in
第一行两个整数n,m。
【输出格式】
输出文件B.out
【样例输入】
4 100
【样例输出】
34
【数据范围】
对于30%的数据,n<=1000000
对于50%的数据,n<=10^9
对于100%的数据,n<=10^100,m<=1000000
想法:第一感觉高精度,然后就一口气写到底,然后。。。。。美妙的。。。。爆零了 QAQ ~~mmp我写了两个小时呀~~
源代码:
#include
using namespace std;
int a[40002]={0,1},s[40002]={0};
int i,n,alen=1,j,slen=1,k,l=1,v=1,m;
int main()
{
freopen("B.in","r",stdin);
freopen("B.out","w",stdout);
cin>>n>>m;
s[1] = 1;
for(k = 1; k <= n; k++) //算阶乘和
{
for(j = 1; j <= alen; j++)
a[j] *= l;
for(j = 1; j <= alen; j++)
if(a[j] >= 10)
{
a[j+1] += a[j] / 10;
a[j] %= 10;
v++;
}
alen++;
while(a[alen] >= 10)
{
a[alen+1] = a[alen] / 10;
a[alen] %= 10;
alen++;
v++;
}
l++;
slen=max(slen,alen);
for(i = 1; i <= slen; i++)
{
s[i] += a[i];
if(s[i] >= 10)
{
if(i == slen) slen++;
s[i] %= 10;
s[i+1]++;
}
}
alen=v;
}
for(i = slen; i >= 1; i--)
if(s[i] == 0 && slen > 1) slen--;
else
break;
unsigned long long x=0;
for(int i = slen; i >= 1; i--) //算余数
x = (x * 10 + s[i]) % m;
if (x == 0)
for (int i = slen; i >= 1; i--)
cout< //写了好久呀~~~(抑扬顿挫的哭声 ) QAQ
std:
#include
#include
#include
#include
#include
using namespace std;
typedef long long ll;
char str[1017];
int main()
{
freopen("B.in","r",stdin);
freopen("B.out","w",stdout);
int t;
ll m;
scanf("%s%I64d",str,&m);
ll len = strlen(str);
ll tmp = 1, tt = 0;
for(int i = 0; i < len; i++)
{
tt = tt * 10 + str[i]-'0';
if(tt >= m) break;
}
if(tt == 0)
{
printf("%I64d\n",1%m);
return 0;
}
if(tt == 1)
{
printf("%I64d\n",2%m);
return 0;
}
ll ans = 2;
for(int i = 2; i <= m && i <= tt; i++) tmp *= i,tmp %= m,ans += tmp,ans %= m;
printf("%I64d\n",ans);
return 0;
}
//这个真的是一个打表题呀QAQ(我还嘲讽了打表的dalao们 )
反思:看到题目了,还是得多想一想,得让草稿纸帮上忙
Problem 3 C(C.cpp/c/pas)
【题目描述】
小明是一个顶级的特工,有一天他得到了一个情报图,记录着敌军的各阵地的最短路径长度信息,情报局有一个网格第i行第j列a[i][j]表示第i个阵地到第j个阵地的最短路径距离。特工想得到一个完整的地图b[i][j]表示第i个阵地到第j个阵地直接连接的双向路的长度(两个阵地之间可以没有路),可能有许多的b[i][j]地图可以满足a[i][j]的最短路径的信息,我们要求路的长度的总长度最短的那个地图。
当然从a[i][j]的最短路径的信息,不一定能合法的地图来对应,如果有合法的地图输出路可能的最短总长度,否则无解输出-1。
【输入格式】
输入文件C.in
输入一行一个整数n表示敌军的阵地数量。
接下来n行,每行n个数,代表a数组,第i行第j列表示第i个城市和第j个城市间的最短路径。
【输出格式】
输出文件C.out
输出一行一个整数表示最短的路的总长度,没有合法方案输出-1。
【样例输入1】
3
0 1 3
1 0 2
3 2 0
【样例输出1】
3
【样例输入2】
3
0 1 3
1 0 1
3 1 0
【样例输出2】
-1
【样例输入3】
5
0 21 18 11 28
21 0 13 10 26
18 13 0 23 13
11 10 23 0 17
28 26 13 17 0
【样例输出3】
82
【数据范围】
对于30%的数据,n<=5;
对于100%的数据,n<=300;
i< >j时1<=a[i][j]=a[j][i]<=10^9;
i = j时a[i][j]=0;
std:
#include
#include
#include
#include
#include
using namespace std;
const int N=305;
int n;
int a[N][N],b[N][N];
int main()
{
freopen("C.in","r",stdin);
freopen("C.out","w",stdout);
scanf("%d",&n);
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++) scanf("%d",&a[i][j]),b[i][j]=(i==j)?0:1e9+1;
for (int i=1;i<=n;i++)
for (int j=i+1;j<=n;j++)
{
bool o=false;
for (int l=1;l<=n;l++)
if (l!=i&&l!=j)
{
if (a[i][l]+a[l][j] 2018.10.2
DAY 3
1.解密
(password.cpp)
(password.in/out)
时间限制:2s/空间限制:256MB
【题目描述】
z老师和w老师正在进行密码的破译工作,他们发现密码是用最基础的凯撒密码加密的,即对于除了‘a’和‘A’以外的字符,都往前推一个字母(如‘b’加密成‘a’,‘X’加密成‘W’),而对于‘a’直接加密成‘z’,‘A’加密成‘Z’。
现在他们打算写一个程序来进行解密,可是这对于他们来说也太简单了,所以他们并不打算自己写这个程序,而是交给你来实现。
【输入格式】
读入只有一行,即已经加密过的文字,是由好几个英文单词组成的句子,每个英文单词只由26个英文字母的大小写构成,词和词之间由空格隔开(可能有多个空格),句末由.结束。(保证没有其他标点符号)
【输出格式】
输出也只有一行,即解密后的文字,需要对格式进行一些整理。
对于多余的空格,请保持原样输出。
除了句首的字母,其他字母一律小写,句首字母强制大写。
【输入输出样例1】
password.in
Hello world.
password.out
Ifmmp xpsme.
【输入输出样例2】
password.in
xnt ITLO H itlo.
password.out
You jump i jump.
【数据规模约定】
对于100%的数据, 1≤n≤100000(N为句子长度)
想法:单纯的模拟题呀,但是我鬼畜的炸了QAQ
源程序
#include
using namespace std;
string str;
int main()
{
freopen("password.in","r",stdin);
freopen("password.out","w",stdout);
bool judge=true;
getline(cin,str);
for (int i = 0; i < str.size(); i++)
{
if (str[i] == 'A')
{
if (judge)
{
judge = false;
cout<<"Z";
}
else
cout<<'z';
}
else
if (str[i] == 'a')
{
if (judge)
{
judge = false;
cout<<"Z";
}
else
cout<<'z';
}
else
if ('A' < str[i] && str[i] <= 'Z' || 'a' < str[i] && str[i] <= 'z')
{
if (judge)
{
judge = false;
if (str[i] > 'a') cout< std:
#include
#include
#include
const int wordsize = 131072;
char words[wordsize];
int main() {
freopen("password.in", "r", stdin);
freopen("password.out", "w", stdout);
gets(words);
int len = strlen(words);
for (int i = 0; i < len; i++)
if (words[i] >= 'A' && words[i] <= 'Z')
words[i] = words[i] - 'A' + 'a';
words[0] = words[0] - 'a' + 'A';
for (int i = 0; i < len; i++)
if (words[i] == 'z')
words[i] = 'a';
else if (words[i] == 'Z')
words[i] = 'A';
else if (words[i] != ' ' && words[i] != '.')
words[i]++;
printf("%s\n", words);
fclose(stdin);
fclose(stdout);
return 0;
}
//但也还是 dalao呀,得orz
//说实话,(这个B的代码写的真丑 ) ,
反思:加强对题意的理解,特别是这种操蛋的题目 ,我还是太弱了呀
2.统计
(sum.cpp)
(sum.in/out)
时间限制:2s/空间限制:256MB
【题目描述】
小Z喜欢自己研究一些问题,今天老师上课讲了相反数,互为相反数的两个数的和为0,小 Z 现在在考虑三个数的情况,小 Z 现在命名三个互不相同且和为 0 的数为“相反数组”,两个相反数组相同当且仅当两个相反字数组的三个数都相同。
现在给定一组数字,求这组数中有多少个相反数组。
【输入格式】
本题读入为多组测试数据!
本题读入为多组测试数据!
本题读入为多组测试数据!
第一行为数据组数T
对于每组测试数据
第一行为数的个数 N
第二行为 N 个数,有正有负
【输出格式】
输对于每组测试数据,输出有多少个不同的相反数组
【输入输出样例1】
sum3.in
1
4
1 1 2 -3
sum3.out
1
【输入输出样例2】
sum3.in
1
3
1 1 -2
sum3.out
0
对于30%的数据,1≤T≤10,1≤N≤1000
对于50%的数据, 1≤T≤10,1≤N≤500
对于100%的数据, 1≤T≤50,1≤N≤1000
想法:三重循环玄学模拟(当然得超时呀,正解还是二分 )
源代码
#include
using namespace std;
long ans;
int a[1009],t,n;
int main()
{
freopen("sum.in","r",stdin);
freopen("sum.out","w",stdout);
cin>>t;
for (int z = 1; z <= t; z++)
{
memset(a,0,sizeof(a));
cin>>n;
for (int i = 1; i <= n; i++)
cin>>a[i];
sort(a+1,a+n+1);
for (int i = 1; i <= n; i++)
for (int j = i+1; j <= n; j++)
if (a[i] == a[j]) a[j] = 0;
else
break;
ans = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
if (a[i] + a[j] + a[k] == 0 && a[i] != a[j] && a[i] != a[k] && a[j] != a[k])
{
if (a[i] != 0 && a[j] != 0 && a[k] != 0)
{
ans++;
//a[i] = 0;
a[j] = 0; //玄学删数,自己都不知道为啥会对
//a[k] = 0;
}
}
cout< std:
#include
#include
const int numsize = 131072;
int T, N;
int a[numsize];
inline int getint() {
register int num = 0;
register char ch = 0, last;
do last = ch, ch = getchar(); while (ch < '0' || ch > '9');
do num = num * 10 + ch - '0', ch = getchar(); while (ch >= '0' && ch <= '9');
if (last == '-') num = -num;
return num;
}
int main() {
freopen("sum.in", "r", stdin);
freopen("sum.out", "w", stdout);
T = getint();
for (int i = 0; i < T; i++) {
N = getint();
for (int i = 1; i <= N; i++)
a[i] = getint();
std::sort(a + 1, a + N + 1);
int cnt = 0;
N = std::unique(a + 1, a + N + 1) - (a + 1);
for (int i = 1; i < N; i++) {// i -> A
int left = i + 1, right = N;
//left -> B, right -> C
while (left < right) {
if (a[i] + a[left] + a[right] == 0) {
left++;
cnt++;
}
if (a[i] + a[left] + a[right] > 0) right--;
if (a[i] + a[left] + a[right] < 0) left++;
}
}
printf("%d\n", cnt);
}
return 0;
}
//二分。。。。。。QAQ》》》》》》GG
反思:二分很重要,得好好练一练
3.恶龙的宝藏
(gold.cpp)
(gold.in/out)
时间限制:2s/空间限制:256MB
【题目描述】
太阳骑士杀死了贪婪魔龙,终于来到了魔龙身后的房间——黄金屋,里面整整齐齐地摆放着一块块山下王国供奉给魔龙的纯金。
黄金屋的平面图可以被看作是一个大小为 N * M 的平面网格图,每个格子里各放着一块黄金(包括起点和终点),黄金的大小不一,重量也有重有轻。魔龙所守护的入口,也就是太阳骑士现在所在的位置是屋子的左上角(1,1),而这间黄金屋的右下角(N,M)是这个屋子的出口,出口外是横跨深渊的龙息长桥,另一端直通山下王国。桥上终年燃烧的魔焰因为魔龙的死亡已经熄灭,可是蚀骨的瘴气依旧盘旋,没有铠甲的保护想通过那里仿佛痴人说梦。
但铠甲上的龙血正在诡异地慢慢渗入,太阳骑士知道这是龙的诅咒,他必须以最快速度回到山下王国的太阳祭坛净化龙血,一旦在黄金屋里浪费太长时间让龙血渗入皮肤,他就会变成下一条恶龙。
最后太阳骑士决定在黄金屋中只往下和往右走,这样通过黄金屋的速度最快,同时他可以顺手捡起经过格子上的黄金(当然也可以不捡起),毕竟不拿点战利品太阳骑士恐怕很难在短期内重新购置他的整套装备。
太阳骑士要考虑的最后一个问题,是负重,他所能携带的最大重量是 K ,时间不允许他估摸着把黄金切成两半,他经过一个格子的时候只能选择捡起或者舍弃,现在他想知道他最多能捡起多少黄金。
【输入格式】
本题读入为多组测试数据!
本题读入为多组测试数据!
本题读入为多组测试数据!
对于每组测试数据,第一行三个数
接下来一个 的矩阵,表示每个格子里的黄金重量
【输出格式】
每组测试数据输出一行答案,即太阳骑士能带走的最大重量的黄金
gold.in
1 1 15
7
3 3 10
6 12 6
6 8 13
2 6 6
3 4 16
5 12 11 7
10 14 10 12
13 10 14 6
gold.out
7
8
16
对于100%的数据, 1≤N,M,K≤100
一个测试点的测试数据组数不会太多,大家放心(cnmb )
想法:感觉可以用记忆化来写(应该也是正解的一种)
源代码
#include
using namespace std;
int dx[3]={0,0,1};
int dy[3]={0,1,0};
int a[109][109],n,m,k,ans,f[109][109];
void search(int x,int y,int sum)
{
if (x < 1 || y < 1 || y > m || x > n) return;
if (sum < f[x][y]) return;
f[x][y] = sum;
if (x == n && y == m)
{
ans = max(ans,sum);
return;
}
for (int i = 1; i <= 2; i++)
if (sum + a[x+dx[i]][y+dy[i]] <= k) search(x+dx[i],y+dy[i],sum+a[x+dx[i]][y+dy[i]]);
else
search(x+dx[i],y+dy[i],sum);
}
int main()
{
freopen("gold.in","r",stdin);
freopen("gold.out","w",stdout);
while(scanf(" %d %d %d",&n,&m,&k)!=EOF)
{
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin>>a[i][j];
memset(f,-1,sizeof(f));
ans = -1;
search(1,1,a[1][1]);
//search(1,1,0); 少了这一种呀。。。。不然就AC了》》QAQ
cout< std:
#include
#include
#include
#include
#include
using namespace std;
int N, M, K;
bool dp[2][105][105];
void solve(){
memset(dp, 0, sizeof(dp));
int pre = 0, cur;
for(int i = 0; i <= M; i++) {
dp[pre][i][0] = true;
}
int get;
for(int r = 0; r < N; r++) {
cur = 1- pre;
for(int i = 0; i <= M; i++)
for(int j = 1; j <= K; j++)
dp[cur][i][j] = false;
dp[cur][0][0] = true;
for(int i = 1; i <= M; i++) {
scanf("%d", &get);
dp[cur][i][0] = true;
for(int j = 0; j <= K; j++) {
if(dp[pre][i][j]) {
dp[cur][i][j] = true;
if(j + get <= K) dp[cur][i][j + get] = true;
}
if(dp[cur][i-1][j]) {
dp[cur][i][j] = true;
if(j + get <= K) dp[cur][i][j + get] = true;
}
}
}
pre = cur;
}
for(int ans = K; ans >= 0; ans--) {
if(dp[pre][M][ans]){
printf("%d\n", ans);
break;
}
}
}
int main(){
freopen("gold.in", "r", stdin);
freopen("gold.out", "w", stdout);
while(scanf("%d%d%d", &N, &M, &K) != EOF)
solve();
return 0;
}
//大佬DP
至今还记得老师发现我们没有写DP后的那一副眉开眼笑的嘴脸,双手挥舞
反思:加强自己的审题,端正态度,不宜以一时写出而装B
4.数组异或
(xorarray.cpp)
(xorarray.in/out)
时间限制:2s/空间限制:256M
【题目描述】
xor——异或,和 and 与or 一样,是一种重要的逻辑运算,他的运算规律是 0 xor 0 = 0,1 xor 1 = 0,1 xor 0 = 1,0 xor 1 = 1
两个整数之间的异或是将两个整数转化成二进制,对他们的每一位分别进行 xor 操作,例:6(110) xor 13(1101) = 11(1011)
现在我们要介绍一种新的操作——数组异或,将两个相同大小(假设都为n)的数组A、B异或成一个新数组C,则新数组必满足:
现在给你数组大小n,和两个数组A,B
求他们的异或数组C
由于最终答案可能过大,你需要对C的每个元素对109+7取模
【输入格式】(xorarray.in)
一共3行。
第一行一个正整数 。
接下来两行每行 个正整数,表示数组A、B。
【输出格式】(xorarray.out)
一共 行, 个正整数,表示数组C。
xorarray.in
7
20670 1316 25227 8316 21095 28379 25235
19745 6535 14486 5460 15690 1796 12403
xorarray.out
7583 52096 161325 276944 453024 675974 958287
对于50%的数据,N≤1000;
对于全部的数据, N≤10^5;
std:
#include
const int ARRSIZE = 131072;
const int mod = 1000000007;
int n;
int A[ARRSIZE], B[ARRSIZE];
int a[32][2], b[32][2];
long long C[ARRSIZE];
int main() {
freopen("xorarray.in", "r", stdin);
freopen("xorarray.out", "w", stdout);
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &A[i]);
for (int i = 1; i <= n; i++)
scanf("%d", &B[i]);
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= 30; j++) {
a[j][(A[i] >> j) & 1]++;
b[j][(B[i] >> j) & 1]++;
long long c = 1ll * a[j][0] * b[j][1] + 1ll * a[j][1] * b[j][0];
c = c % mod;
c = c * (1 << j) % mod;
C[i] = (C[i] + c) % mod;
}
}
for (int i = 1; i <= n; i++)
printf("%d ", C[i]);
putchar('\n');
fclose(stdin);
fclose(stdout);
return 0;
}
2018.10.3
DAY 4
1.RPG
(souls.cpp)
(souls.in/out)
时间限制:2s/空间限制:256MB
【题目描述】
小T最近沉迷于一款ACRPG已久,他发现这个ACRPG的伤害计算是十分复杂的一个系统,他想你设计一个程序方便他这个深度数据控计算伤害点数。
以下是简化后的伤害计算法则:
由于是简化版本所以只计算单一属性伤害,我们将给出你的攻击力和对面的防御力,首先你需要先计算攻防比 K = 你的攻击力 / 对面的防御力。
如果 K < 1 / 8,那么你造成的实际伤害为恒定值 2.
如果 1 / 8 <= K < 1 / 2,那么你造成的伤害为 0.125 * 你的攻击力
如果 1 / 2 <= K < 1,那么你造成的伤害为 0.333 * 你的攻击力
如果 1 <= K < 2,那么你造成的伤害为 你的攻击力 * sqrt(对手的防御力 / 你的攻击力)
如果 2 <= K < 8,那么你造成的伤害为 你的攻击力^2 / (2*对手的防御力)
如果 K >= 8,那么你造成的伤害为恒定的 8 * 你的攻击力
最终伤害如果有小数,全部按下取整
【输入格式】
读入为多组测试数据
第一行为测试数据组数 T
接下来 T 行有两个正整数,
第一个数为你的攻击力,第二个数为对面的防御力。
【输出格式】
输出一共为 T 行。
为你对对面的实际伤害,都是整数,请按下取整。
【输入输出样例1】
souls.in
2
5 5
1000 10
souls.out
5
8000
【输入输出样例2】
souls.in
3
591 345
953 706
814 61
souls.out
451
820
6512
【数据规模约定】
对于100%的数据,你的攻击力和对面的防御力都不超过 10 ^ 7。
想法:送分水题,我应该打小数的,不该打这种类似分数的东东。。。QAQ
源代码
#include
using namespace std;
double a,b,k,total;
int t;
int main()
{
freopen("souls.in","r",stdin);
freopen("souls.out","w",stdout);
cin>>t;
for (int i = 1; i <= t; i++)
{
cin>>a>>b;
k = a / b;
if (k < 1 / 8) total = 2;
else
if (1 / 8 <= k && k < 1 / 2) total = 0.125 * a;
else
if (1 / 2 <= k && k < 1) total = 0.333 * a;
else
if (1 <= k && k < 2) total = a * sqrt(b / a);
else
if (2 <= k && k < 8) total = a * a / (2 * b);
else
if (k >= 8) total = 8 * a;
cout< std:
#include
#include
int T;
int a, b, ans;
int main() {
freopen("souls.in", "r", stdin);
freopen("souls.out", "w", stdout);
scanf("%d", &T);
for ( ; T; T--) {
scanf("%d %d", &a, &b);
if (8 * a < b) ans = 2;
else if (2 * a < b) ans = int(0.125 * a);
else if (a < b) ans = int(0.333 * a);
else if (a < 2 * b) ans = int(a * sqrt(1.0 * b / a));
else if (a < 8 * b) ans = int(0.5 * a * a / b);
else ans = 8 * a;
printf("%d\n", ans);
}
return 0;
}
反思:学习到小数与这种写法的不同,加强改进,不能再犯这一种低级错误了
2.二次迭代数列
(sequence.cpp)
(sequence.in/out)
时间限制:2s/空间限制:256MB
【题目描述】
小 F 特别喜欢研究数列,并给各种各式各样的数列取个自己喜欢的名字。
最近老师上课讲到了二次函数的一般形式 F(x) = a * x ^ 2 + b * x + c
小 F 就想把二次函数和自己最新研究出的迭代数列组合一下。
迭代数列即通过一个函数 A(x) 和数列的初值a1得到整个数列:
am = A(an-1)
小 F 想如果 A(x) 是一个二次函数,那么就将得到的数列命名为二次迭代数列。
小 F 想研究这个数列的通项性质,但是他又不会计算这个数列。
现在他把这个数列的 a1、a、b、c 都告诉你,希望你能帮他计算这个数列的第 n 项。
不过小 F 是个很怕麻烦的人,不想对着太大的数字发呆,所以他希望你能告诉他最终答案 mod p后的结果,他可以研究 mod p 后的性质。
【输入格式】
读入一共一行,6 个整数
从左到右
a1 a b c n p
其中 n 和 p 一定是正整数
【输出格式】
输出一共一行,即答案,答案请不要出现负数。
【输入输出样例1】
sequence.in
2 2 2 2 10 127
sequence.out
2
【输入输出样例2】
sequence.in
3 3 3 3 10 127
sequence.out
123
【数据规模约定】
对于30%的数据,n不超过 10 ^ 7。
对于100%的数据,n 不超过 10 ^ 17,p 不超过 2 * 10 ^ 6。
想法:自己瞎写了一个线性的,然后不知为何鬼畜的WA了。。。QAQ
源代码
#include
using namespace std;
long long last,total;
long a,b,c,n,p;
int main()
{
freopen("sequence.in","r",stdin);
freopen("sequence.out","w",stdout);
cin>>last>>a>>b>>c>>n>>p;
for (int i = 2; i <= n; i++)
{
total = (a * last * last + b * last + c) % p;
if (total < 0) total += p;
last = total;
}
cout< STD
#include
#include
const int mod = 2097152;
int F(int x, int a, int b, int c, int p) {
long long ans = a;
ans = ans * x % p * x % p;
ans = (ans + b * x % p) % p;
ans = (ans + c) % p;
ans = (ans + p) % p;
return ans;
}
int a1, a, b, c, p;
long long n;
int f[mod];
int g[mod];
int main() {
freopen("sequence.in", "r", stdin);
freopen("sequence.out", "w", stdout);
scanf("%d %d %d %d %lld %d", &a1, &a, &b, &c, &n, &p);
a1 = (a1 % p + p) % p;
memset(g, 0, sizeof(g));
f[1] = a1, g[a1] = 1;
int point = 0;
for (int i = 2; true; i++) {
if (i > n) break;
f[i] = F(f[i - 1], a, b, c, p);
if (g[f[i]]) {
point = i;
break;
}
g[f[i]] = i;
}
if (!point)
printf("%d\n", f[n]);
else {
int m = g[f[point]] - 1, l = point - g[f[point]];
n -= m;
n %= l;
if (n == 0) n = l;
printf("%d\n", f[m+n]);
}
return 0;
}
//这是一道规律题呀!!!!
反思:没啥想说的但要加强自己的递推运算能力
.我去买个橘子
(square.pas/c/cpp)
(square.in/out)
时间限制:2s/空间限制:256MB
【题目描述】
“ 好玩吗?
会玩了吗?
还玩吗?”
张大喵有个正在上初中的表弟橘子哥,正如他的名字一样,这个人非常非常喜欢给自己买橘子。
这天,橘子哥同学正在学习因式分解,老师在课后写了好几个基本公式在黑板上要求同学们熟练掌握,第一个就是大家耳熟能详的 。橘子哥忽然又按捺不住秀的欲望,下课的时候他故意把黑板上的 改成了 。就在橘子哥沾沾自喜的时候,被回到教室的老师当场逮住。
老师很愤怒,于是他给橘子哥布置了额外的作业作为惩罚——橘子哥必须回答出有多少个数对 满足:
- ;
- 是一个完全平方数;
橘子哥——当然是完全不会做,但是他希望他能继续蒂花之秀。所以他求求你帮帮他,不然看热闹的同学们一定会对他进行疯狂的嘲讽(我去给你买个橘子),他就无法继续独秀下去。如果他成功给出答案,一定能得到同学们的夸奖(都是九年级义务教育,为啥你就这么优秀)所以你已经是他最后的救命稻草了。
【输入格式】
共一行,一行两个数,A、B
【输出格式】
共一行,一行数,即问题的答案
【输入输出样例1】
square.in
10 10
square.out
12
【输入输出样例2】
square.in
60 400
square.out
389
【数据规模约定】
对于30%的数据, 1≤A,B≤10^3
对于100%的数据, 1≤A,B≤10^6
想法:暴力(因为我只会暴力 )能搞到30分,很划算
源代码:
#include
using namespace std;
long ans;
int a,b;
int main()
{
freopen("square.in","r",stdin);
freopen("square.out","w",stdout);
cin>>a>>b;
for (int x = 1; x <= a; x++)
for (int y = 1; y <= b; y++)
{
long long sum = x * x + 2 * y + 1;
if (int (sqrt(sum)) * int (sqrt(sum)) == sum) ans++;
}
cout< STD
#include
#include
typedef long long llint;
int main()
{
llint A, B;
llint ans = 0;
freopen("square.in", "r", stdin);
freopen("square.out", "w", stdout);
scanf("%lld %lld", &A, &B);
for (llint i = 1; i <= A; i++)
for (llint j = i, k = 1; j <= B; j += (i << 1) + (k << 2), k++)
ans++;
printf("%lld\n", ans);
return 0;
}
这又是一个该死的数学题
反思:。。。。。。要注重草稿纸上的运算。。。用思维复杂度换时间与内存复杂度
4.宸独秀的约瑟夫
(killgame.cpp)
(killgame.in/out)
时间限制:2s/空间限制:256MB
【题目描述】
豹妹收到了灯妹的邀请,在国庆节前往非洲的尼古拉斯国游玩。
没想到这是一次灯妹的复仇计划,灯妹早就对豹妹在群中疯狂的无意识海豹行为十分嫉妒,于是她将豹妹带去了严禁晒卡的尼古拉斯国。
果然豹妹才刚到机场就因为无意识的海豹行为被尼古拉斯猎豹警察逮捕。
猎豹警察的顶头上司名为宸独秀,是个血统纯正的非洲人,拥有无上权力的他却永远出不了SSR,所以他恨透了海豹,他认为没有智商空有运气的海豹是导致社会不安定的毒瘤。所以他每次都会等被逮捕的海豹达到一定数量后和他们玩一个测试——即他自己发明的宸独秀的约瑟夫杀人游戏,只有最聪明的海豹才能站在最正确的位置活下来,这样他就证明了自己对社会的价值,就不会被处刑。
现在一共有 n 个人,这个杀人游戏和约瑟夫几乎没有区别:
第一轮,第一人从 1 开始报数,报到 1 就停止且那个人立刻出局
第二轮,出局者的下一人从 1 开始报数,报到 2 就停止且那个人立刻出局
第三轮,出局者的下一人从 1 开始报数,报到 3 就停止且那个人立刻出局
第四轮,出局者的下一人从 1 开始报数,报到 4 就停止且那个人立刻出局
……
以此类推,直到剩下最后一人为止。
豹妹一眼看穿了她是不能站在第一人的,但是她不清楚她站在哪个位置是最安全的,所以豹妹求助于你,你能帮帮她吗?
——海豹歌节选
小小海豹江中游,两件大事记心头,
如欲十连先预警,只需一宝必单抽,
自古多肝无益处,从来海豹不秃头,
…………………………
可怜楼上豹徘徊,应照非洲偷渡台,
一顿豹打打不尽,明天抽卡复还来。
【输入格式】
本题目为多组测试数据
第一行为数据组数 T
接下来 T 行,每行一个正整数 n
【输出格式】
输出一共 T 行
每行一个数字,即答案。
【输入输出样例1】
killgame.in
2
2
3
killgame.out
2
2
【输入输出样例2】
killgame.in
2
274
467
killgame.out
138
427
【数据规模约定】
对于30%的数据,T <= 5, n不超过 500。
对于100%的数据,T 不超过 5000,n 不超过 5000。
想法:本能打表,但是某个嘴贱的走漏了风声,被老师卡了,无奈暴力
源代码
#include
using namespace std;
bool a[5001]={0};
int T,m,f,t,s,n;
int main()
{
freopen("killgame.in","r",stdin);
freopen("killgame.out","w",stdout);
cin>>T;
for (int i = 1; i <= T; i++)
{
cin>>n;
m = 1;
f = 0;
t = 0;
s = 0;
memset(a,0,sizeof(a));
do
{
++t;
if(t > n) t = 1;
if(!a[t]) s++;
if(s == m)
{
s = 0;
a[t] = 1;
f++;
m++;
}
}
while(f < n);
cout< std
老师说,他的方法并不是非常好,让我们用一个dalao的算法来写:
{
a[1] = 1;
for (int i = 2; i <= 5000; i++)
{
ans = 0;
for (int j = 2; j <= i; j++)
ans = (ans + i - j + 1) % j;
a[i] = ans;
}
反思:。。。。。。。还是要多注意对数据的研究
2018.10.4
DAY 5
字符
【问题描述】
输入一个字符串, 输出一个字符串。
要求输出的字符串中每个位置上的字符,应当是输入串对应位置的字符的后
一个字符。
如 a->b gbd->hce ts->ut
保证输入没有 z
【输入格式】
一个小写字母组成的字符串
【输出格式】
答案字符串
【样例输入】
abcde
【样例输出】
bcdef
【数据规模和约定】
对于 30%的数据, 输入长度不超过 10
对于 100%的数据, 输入长度不超过 10^5
想法:水题
源代码
#include
using namespace std;
string str;
int main()
{
freopen("wr.in","r",stdin);
freopen("wr.out","w",stdout);
getline(cin,str);
for (int i = 0; i < str.size(); i++)
cout< std
#include
#include
#include
using namespace std;
char a[100500];
int main()
{
freopen("wr.in","r",stdin);
freopen("wr.out","w",stdout);
scanf("%s",a+1);
int len=strlen(a+1);
int i;
for(i=1;i<=len;i++)
putchar(a[i]+1);
return 0;
}
反思:**这一题虽然很简单,但是还是要注意这一种题目的细节,(太容易爆零了!!!笔者感同生受 )
阶乘
【问题描述】
输入 n 个正整数, a1,a2,…,an。
正整数 x 的阶乘是 x!=12…*x
求 a1!*a2!a3!…*an!
答案对 10^9+7 取模
【输入格式】
第一行一个数 n
第二行 n 个数 a1,a2,…,an
【输出格式】
一个数表示答案
【样例输入】
3
3 4 2
【样例输出】
288
【数据规模和约定】
对于 30%的数据, n<=10
对于 60%的数据, n<=1000
对于 100%的数据, n<=10^5, ai<=10^6
想法:*吸取了前几次的教训,发现了可以写线性的记忆化算法,很快,很好想到(我也是灵机一动) *
源代码
#include
using namespace std;
const int mod = 1000000007;
long long f[100009];
int a[100009],n;
long long ans;
int main()
{
freopen("fact.in","r",stdin);
freopen("fact.out","w",stdout);
cin>>n;
for (int i = 1; i <= n; i++)
cin>>a[i];
sort(a+1,a+n+1);
f[1] = 1;
for (int i = 1; i <= a[1]; i++)
f[1] = (f[1] * i) % mod;
ans = f[1];
for (int i = 2; i <= n; i++)
{
f[i] = f[i - 1];
for (int j = a[i - 1] + 1; j <= a[i]; j++) //存下前面的,后面直接用
f[i] = (f[i] * j) % mod;
ans = (ans * f[i]) % mod;
}
cout< //记忆化大法好!!!!
STD
#include
#include
using namespace std;
const int N = 1005000;
const int Mod = 1e9+7;
int xu[N];
int mul(int x,int y)
{
long long z=x;
z*=y;
z%=Mod;
x=z;
return x;
}
int main()
{
freopen("fact.in","r",stdin);
freopen("fact.out","w",stdout);
int i;
xu[0]=1;
for(i=1;i 反思:注意对自己程序如记忆化这种高度优化的练习,继续加油!!!
小球
【问题描述】
有 n 个小球, 编号为 1~n。
有 m 种颜色,编号为 1~m。
现在要给每个小球染一种颜色。要求每种颜色都要用到(即每种颜色的小球
都至少有一个)。
求方案数,对 x 取模。
【输入格式】
一行三个数, n、 m、 x
【输出格式】
一行一个数, 答案
【样例输入】
4 3 50
【样例输出】
36
【数据规模和约定】
对于 30%的数据, n<=20, m=3
对于 60%的数据, n<=20
对于 100%的数据, 1<=m<=n<=1000, 2<=x<=10^9
想法:*自己觉得是排列组合,但是正解是DP,mmp *
源代码
#include
using namespace std;
long n,m,mod;
long long ans = 1;
int main()
{
freopen("ball.in","r",stdin);
freopen("ball.out","w",stdout);
cin>>n>>m>>mod;
for (int i = 1; i <= m; i++)
ans = (ans * i) % mod;
if (m == n)
{
cout<= n-m+1; i--) //自己推的玄学递推式(搞到了10分)
ans = (ans * i) % mod;
cout< STD
#include
#include
using namespace std;
const int N = 1050;
int n,m,p;
int f[N][N];
//f[i][j] denotes the number of solutions to paint i balls with exactly j colors
//here colors are identical
int main()
{
freopen("ball.in","r",stdin);
freopen("ball.out","w",stdout);
scanf("%d%d%d",&n,&m,&p);
int i,j;
f[0][0]=1;
f[1][0]=0;
f[1][1]=1;
for(i=2;i<=n;i++)
{
f[i][0]=0;
f[i][1]=1;
for(j=2;j 反思:加强自己对玄学递推式的运算 DP还是的学呀。。。。
想法:*直接敲暴力,不啰嗦(因为我只会这个 ),同时判断一下素数(我从这个小细节了捞到30分,美滋滋 )
源代码
#include
using namespace std;
int x;
int ans = 0;
bool judge;
int main()
{
freopen("divisor.in","r",stdin);
freopen("divisor.out","w",stdout);
cin>>x;
for (int i = 2; i <= int(sqrt(x)); i++) //骗分神器,30分哈哈哈
if (x % i == 0)
{
judge = true;
break;
}
if (!judge)
{
cout<<3;
return 0;
}
else
for (int i = 1; i <= x; i++)
if (x % i == 0)
{
int ans1 = 0;
for (int j = 1; j <= i; j++)
if (i % j == 0) ans1++;
ans += ans1;
}
cout< STD
#include
#include
#include
using namespace std;
int main()
{
freopen("divisor.in","r",stdin);
freopen("divisor.out","w",stdout);
long long ans=1;
int n,i;
cin>>n;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
{
long long now=0;
while(n%i==0)
{
now++;
n/=i;
}
now=(now+2)*(now+1)/2;
ans*=now;
}
}
if(n>1)
ans*=3;
cout< 反思:我得死背数论式
2018.10.5
DAY 6
邮件
【问题描述】
有 n 个人, 他们两两之间互相发邮件, 问一共发了多少封邮件
【输入格式】
一个数 n
【输出格式】
一个数, 多少封邮件
【样例输入】
6
【样例输出】
30
【数据规模和约定】
对于 30%的数据, 1<=n<=1000
对于 60%的数据, 1<=n<=10^6
对于 100%的数据, 1<=n<=10^9
想法:简单的数学题,很容易推出公式
源代码
#include
using namespace std;
long long n,total;
int main()
{
freopen("mail.in","r",stdin);
freopen("mail.out","w",stdout);
cin>>n;
total = n * (n - 1);
cout< STD
#include
#include
#include
using namespace std;
int main()
{
freopen("mail.in","r",stdin);
freopen("mail.out","w",stdout);
int n;
cin>>n;
long long ans=n;
ans*=(n-1);
cout< 反思:加强自己对数学式子的推导能力
除法
【问题描述】
有一个游戏, 最初你有 n 个正整数。
每当你使用一个数,可以得到一些能量。如果你使用了数 a,而且你剩下的
数(包括正在使用的 a)中有 x 个数是 a 的约数,那么你能得到 x 点能量。使用
a 过后这个 a 就消失了。
你可以把 n 个数全部用完。
求最多获得多少能量。
【输入格式】
第一行 n
第二行 n 个数
【输出格式】
最大能量数
【样例输入】
5
1 3 5 9 3
【样例输出】
12
(用的顺序可以是: 9 3 3 5 1)
【数据规模和约定】
对于 30%的数据, n<=10
对于 60%的数据, n<=1000
对于 100%的数据, n<=10^6, 所有数不超过 10^6
想法:暴力,自己会也只会。。。。。。。。
源代码
#include
using namespace std;
long a[10000009];
int ans,n;
int main()
{
freopen("div.in","r",stdin);
freopen("div.out","w",stdout);
cin>>n;
for (int i = 1; i <= n; i++)
cin>>a[i];
sort(a+1,a+n+1);
for (int i = n; i >= 1; i--)
for (int j = 1; j <= i; j++)
if (a[i] % a[j] == 0) ans++;
cout< STD
#include
#include
#include
using namespace std;
const int N = 1e6+3;
int tot[N];
long long divs[N];
long long self[N];
long long ans;
int n;
int main()
{
freopen("div.in","r",stdin);
freopen("div.out","w",stdout);
int i,j;
scanf("%d",&n);
for(i=1;i<=n;i++)
{
int now;
scanf("%d",&now);
tot[now]++;
}
for(i=1;i<=n;i++)
self[i]=self[i-1]+i;
for(i=1;i 反思:。。。。(水过去吧。。。写不出来)
网络
【问题描述】
在计算机科学中,经常要通过分析变量之间的相关性来简化计算过程。变量
间的相关性可以用有向图 G=(V,E)来表示,图中的点表示变量,边表示变量间
的关系。这里 G 满足: G 中的所有边都从编号小的点指向编号大的点。
从图中选出一个点集 T⊆V,如果 T 中的任意两个点之间都有边(方向是编
号小的点指向编号大的点),则称 T 为团。特别地,空集也认为是一个团。
如果存在一个点,与 T 中的任意一个点之间都有边(方向是编号小的点指
向编号大的点),那么称 T 为可扩团。
如果一个团 S 不是可扩团,那么称它为极大团。
给出 G,求 G 有多少个不同的极大团。
这里 G 满足一个性质:对于 G 中任意一个点 i, 用 H[i]表示编号比 i 小的点
中所有与 i 有边相连的点的集合,那么 H[i]是一个团。
【输入格式】
第一行 n, m,表示点数和边数
接下来 m 行,每行两个数 a, b,表示有从 a 到 b 的边
注意可能有重边
保证输入的图满足问题描述中提到的性质。
【输出格式】
极大团数量
【样例输入】
4 5
1 2
1 3
2 3
2 4
3 4
【样例输出】
2
【数据规模和约定】
对于 30%的数据, n<=10
对于 60%的数据, n<=1000
对于 100%的数据, n,m<=1000000
STD
#include
#include
using namespace std;
const int N = 1000500;
struct Edge
{
int a,b;
}edge[N];
int last[N];
int tot[N];
bool inva[N];
int n,m;
bool cmp(Edge x,Edge y)
{
if(x.ay.a) return 0;
return (x.b=1;i--)
{
if(last[i])
{
if(tot[i]>tot[last[i]])
inva[last[i]]=1;
}
}
int ans=0;
for(i=1;i<=n;i++)
{
if(!inva[i])
ans++;
}
printf("%d\n",ans);
return 0;
}
线段
【问题描述】
数轴上有 n 条线段, 第 i 条线段的左端点是 a[i],右端点是 b[i]。
Bob 发现 1~2n 共 2n 个整数点,每个点都是某条线段的端点。
这些线段有如下两类特点:
1 a b,表示第 a 条线段和第 b 条线段相交
2 a b,表示第 a 条线段在第 b 条线段的左边,且它们不相交。
共有 m 个特点,每个特点都是如上两类之一。
Bob 想通过这些特点推理得到每条线段的端点。
【输入格式】
第一行两个正整数 n, m
接下来 m 行,每行三个正整数,描述线段的特点,格式见题目描述
【输出格式】
输出 n 行, 第 i 行两个正整数, 用空格隔开, 分别是 a[i]和 b[i]
可能有多种答案,输出字典序最小的答案。即先要求 a[1]最小,若仍有多解
再要求 b[1]最小,若仍有多解再要求 a[2]最小,若仍有多解再要求 b[2]最小,若
仍有多解再要求 a[3]最小……
如果无解输出“Wrong”(不输出引号)。
【样例输入】
3 2
1 2 3
2 1 3
【样例输出】
1 2
3 5
4 6
【数据规模和约定】
对于 30%的数据, 1<=n,m<=10
对于 60%的数据, 1<=n,m<=1000
对于 100%的数据, 1<=n,m<=100000
STD
#include
#include
#include
#include
#include
using namespace std;
const int N = 300500;
int point[N],to[N],next[N],cc;
int dui[N],dcc;
int ru[N];
int sc[N];
int n,m;
void AddEdge(int x,int y)
{
cc++;
next[cc]=point[x];
point[x]=cc;
to[cc]=y;
ru[y]++;
}
void Add(int x)
{
dcc++;
int now=dcc;
int next=now/2;
while(next && dui[next]dui[next])
next++;
while(nextdui[dcc])
{
dui[now]=dui[next];
now=next;
next=now*2;
if(next+1dui[next])
next++;
}
dui[now]=dui[dcc];
dcc--;
return val;
}
int main()
{
freopen("seg.in","r",stdin);
freopen("seg.out","w",stdout);
int i,j;
cin>>n>>m;
while(m--)
{
int a,b,c;
cin>>c>>a>>b;
if(c==1)
{
AddEdge(a*2,b*2-1);
AddEdge(b*2,a*2-1);
}
else
AddEdge(b*2-1,a*2);
}
for(i=1;i<=n;i++)
AddEdge(i*2,i*2-1);
n*=2;
for(i=1;i<=n;i++)
{
if(!ru[i])
Add(i);
}
for(i=n;i>=1;i--)
{
if(!dcc)
{
printf("Wrong\n");
return 0;
}
int now=Del();
int then=point[now];
while(then)
{
int tox=to[then];
ru[tox]--;
if(!ru[tox])
Add(tox);
then=next[then];
}
sc[now]=i;
}
for(i=1;i<=n;i++)
{
cout< 最后一次的模拟考了,7日国庆假期用来换这些绝妙的体验很值,也许在未来,这将化为更久远的回忆吧。。。。。。。。。
2018.10.6
