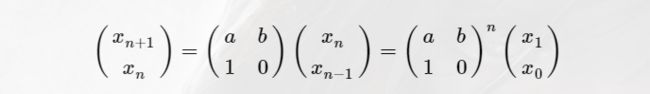2019牛客暑期多校训练营（第五场）B generator 1 十进制矩阵快速幂

传送门

题意：给你x0、x1 a、b、mod，根据  求出

思路：
​ 

用十进制

设  为res 则可得

我们再设

就是分解n为每一位，再去相乘。

例如 

讲计算出来的即可

#include
#include
#include
#include
#include
#define ll long long 
using namespace std;
struct mat
{
    ll m[10][10];
};
char n[1000100];
ll mod;
mat mul(mat x,mat y)
{
    mat c;
    for(int i=0;i<2;i++)
	{
		for(int j=0;j<2;j++)
		{
			c.m[i][j]=0;
		}
	}
    for(int i=0;i<2;++i){
        for(int j=0;j<2;++j){
            for(int k=0;k<2;++k){
                c.m[i][j] = (c.m[i][j]%mod + x.m[i][k]*y.m[k][j]%mod)%mod;
            }
        }
    }
    return c;
}
mat pow(mat x,int y)//矩阵快速幂
{
    mat ans;
    for(int i=0;i<2;i++)
	{
		for(int j=0;j<2;j++)
		{
			if(i==j)
			ans.m[i][j]=1;
			else
			ans.m[i][j]=0;
		}
	}
    while(y){
        if(y&1) ans = mul(ans,x);
        x = mul(x,x);
        y>>=1;
    }
    return ans;
}
mat pow10(mat A,char *s)
{
	int len=strlen(s)-1;
	mat B;
	for(int i=0;i<2;i++)
	{
		for(int j=0;j<2;j++)
		{
			if(i==j)
			B.m[i][j]=1;
			else
			B.m[i][j]=0;
		}
	}
	for(int i=len;i>=0;i--)
	{
		if(s[i]-'0'>0)
		{
			mat x=(pow(A,s[i]-'0'));
			B=mul(B,x);
		}
		A=pow(A,10);
	}
	return B;
}
int main()
{
	ll x0,x1,a,b;
	cin>>x0>>x1>>a>>b;
	mat mm;
	mm.m[0][0]=a,mm.m[0][1]=b;
	mm.m[1][0]=1,mm.m[1][1]=0;
	scanf("%s",n);
	cin>>mod;
	mm=pow10(mm,n);
	ll ans=((x1*mm.m[1][0])%mod+(x0*mm.m[1][1]%mod))%mod;
	printf("%lld\n",ans);
	return 0;
}