hdu-1016 Prime Ring Problem(素数环) DFS解法

Prime Ring Problem

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 42172    Accepted Submission(s): 18682

Problem Description

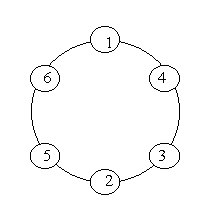
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.

Note: the number of first circle should always be 1.

 

Input

n (0 < n < 20).

 

Output

The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.

You are to write a program that completes above process.

Print a blank line after each case.

 

Sample Input

6 8

 

Sample Output

Case 1: 1 4 3 2 5 6 1 6 5 2 3 4 Case 2: 1 2 3 8 5 6 7 4 1 2 5 8 3 4 7 6 1 4 7 6 5 8 3 2 1 6 7 4 3 8 5 2

题目大意是输入一个n，n在0-20之间，将1-n所有数插入一个环中，使环内相邻元素相加为素数。可以将1固定在第一个位置，然后在进行dfs找出其他的可能，具体代码如下(代码有一些注释解释做法)：

//
//  main.cpp
//  hdu1016
//
//  Created by Morris on 16/7/20.
//  Copyright © 2016年 Morris. All rights reserved.
//

#include  
#include 

#define PRIME_SZ 40
#define VISIT_SZ 20

namespace {
    using std::scanf;
    using std::printf;
    using std::memset;
}

//数据量少，直接记录素数表就好了
int prime[PRIME_SZ] = {0,0,1,1,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,0,1,0,0};

//记录是否访问过该元素
int visit[VISIT_SZ] = { 0 };

//dfs之后得到的其中一种结果
int arr[VISIT_SZ - 1] = { 0 };

int n;

int is_prime(int num);
void dfs(int index);

int main(int argc, const char *argv[])
{
    int case_num = 0;
    while (~scanf("%d", &n)) {
        ++case_num;
        printf("Case %d:\n", case_num);
        
        //有多组测试数据，要注意visit数组每次都要重新赋值0
        memset(visit, 0, sizeof(visit));
        arr[0] = 1;
        dfs(1);
        printf("\n");
    }
    
    return 0;
}

void dfs(int num)
{
    //num == n时，说明素数环已填充到了最后一个位置，判断与开头位置是否满足条件，把判断放在这是因为开头固定死了是1
    //不满足条件则将回溯
    if (num == n && prime[arr[num - 1] + arr[0]] == 1) {
        int i;
        //满足条件之后，说明其中一种结果已经求出来了，将结果打印出来
        for (i = 0; i < num - 1; ++i) {
            printf("%d ", arr[i]);
        }
        
        printf("%d\n", arr[num - 1]);
    }
    else {
        int i;
        for (i = 2; i <= n; ++i) {
            //判断元素是否被访问过，避免结果中出现重复元素
            if (visit[i] == 0) {
                //判断当前访问元素与环中前一位置的元素和是否为素数
                if (prime[i + arr[num - 1]] == 1) {
                    //前进的过程
                    visit[i] = 1;
                    arr[num++] = i;
                    dfs(num);
                    
                    //回溯的过程，将标记消去
                    visit[i] = 0;
                    num--;
                }
            }
        }
    }
}