扫描线求矩形覆盖面积--入坑总结

扫描线思想：扫描线算法

被覆盖1次的区域面积

扫描线一个很经典的例题（HDU-1542-Atlantis）：在坐标轴上有若干个矩形，问他们覆盖的面积总和。
因为他们覆盖的面积有重复，于是就用到了神奇的扫描线算法。

扫描线一般就是平行于x轴或者y轴的直线。通过这些直线我们可以把这些矩形覆盖的区域分成若干个子区域分别求面积最后再求和，如下图的区域就被分成了5个子区域。（我是以x轴建的线段树）

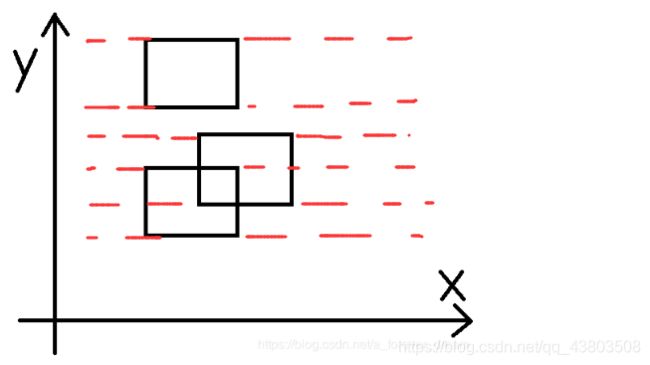
要求得这些子区间的面积，重点就在于求每个子区间被覆盖的区间长度和。扫描线向上移动每遇到一条矩形的边，就意味着一段连续的区间会被这个矩形覆盖，或者这段连续的区间不再被这个矩形覆盖。这样就变成了一个区间修改的问题。遇到矩形的下边，这段区间的覆盖次数就加一；遇到矩形的上边，这段区间的覆盖次数就减一，每次统计整段区间上被覆盖过的区间长度。

还有一点是，因为题目中的横坐标值比较大，且是浮点数，所以需要离散化一下。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define mid ((l + r)>>1)
#define chl root<<1
#define chr root<<1|1
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int manx=510;
double tree[manx<<2],X[manx<<1];
int cover[manx];
//tree维护的是1-n中被覆盖的区间长度和
//X存的是所有矩形顶点的横坐标，最后要离散化
//cove维护每个区间被覆盖的次数
struct node
{
    double y,lx,rx;
    int val;
    friend bool operator<(node a,node b)
    {
        return a.y<b.y;
    }
    //node(double a=0,double b=0,double c=0,int d=0):y(a),lx(b),rx(c),val(d){}
}line[manx<<1];
//存矩形上下边的信息，每条边会对应一次区间修改
void init()
{
    memset(tree,0,sizeof(tree));
    memset(cover,0,sizeof(cover));
}
void eval(int root,int l,int r)
{
    if(cover[root])
        tree[root]=X[r+1]-X[l];
    else tree[root]=tree[chl]+tree[chr];
}
void change(int root,int l,int r,int ll,int rr,int val)
{
//这里有些地方写的是l>=ll&&r<=rr的判断条件，他们的区别就在于一个是分的要查询的区间，一个是分的被查询区间(即1-n的区间)
//我分的是要查询的区间(ll-rr)，仔细看会发现这两种写法在下面else中的change里的传参是不一样的
    if(l==ll&&r==rr)
    {
        cover[root]+=val;
        eval(root,l,r);
        return;
    }
    if(rr<=mid)
        change(chl,l,mid,ll,rr,val);
    else if(ll>mid)
        change(chr,mid+1,r,ll,rr,val);
    else
    {
        change(chl,l,mid,ll,mid,val);
        change(chr,mid+1,r,mid+1,rr,val);
    }
    eval(root,l,r);
}
int main()
{
    int n,Cas=0;
    double x1,y1,x2,y2;
    while(scanf("%d",&n),n)
    {
        double ans=0;
        init();
        for(int i=1;i<=n;i++)
        {
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            line[i*2]=node{y1,x1,x2,1};
            X[i*2]=x1;
            line[i*2-1]=node{y2,x1,x2,-1};
            X[i*2-1]=x2;
        }
        sort(X+1,X+2*n+1);
        sort(line+1,line+2*n+1);
        int cnt=unique(X+1,X+2*n+1)-X-1;
        for(int i=1;i<2*n;i++)
        {
            int l=lower_bound(X+1,X+cnt+1,line[i].lx)-X;
            int r=lower_bound(X+1,X+cnt+1,line[i].rx)-X-1;
            double dy=line[i+1].y-line[i].y;
            change(1,1,cnt,l,r,line[i].val);
            ans+=tree[1]*dy;
        }
        printf("Test case #%d\nTotal explored area: %.2f\n\n",++Cas,ans);
    }
    return 0;
}

被覆盖2次的区域面积

例题：HDU-1255-覆盖的面积

（正解直接搬吧）hdu 1255 覆盖的面积

最开始写了一个假的线段树+扫描线算法过了，但是看代码跑出来的时间有点长。最后发现我把它写成了一个暴力的单点修改：当时我只用了一个tree数组维护被覆盖了2次的区间长度，cover数组维护区间段上被覆盖的最少次数，还维了一个lazy数组。后面又改了半天发现这个思路好像实现不了（我觉得是实现不了）。因为cover>=2的时候好说，可以直接计算长度，但是=1的时候去不能像上面的例题一样通过左右子区间求解，因为区间修改中push_down只能操作到我们要找的那个区间，就算push_down lazy的值也可能会遗漏计算被覆盖两次上的区间，除非push_down到叶子结点（可能这就是7.63的答案总是测出7.50的结果的原因吧）

所以还是得再开一个tree数组维护被覆盖了1次的区间长度。

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f
#define mid ((l + r)>>1)
#define chl root<<1
#define chr root<<1|1
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
const int manx=11000;
double tree[manx<<2],X[manx<<1],tree2[manx];//lazy[manx],
int cover[manx];
struct node
{
    double y,lx,rx;
    int val;
    friend bool operator<(node a,node b)
    {
        return a.y<b.y;
    }
    //node(double a=0,double b=0,double c=0,int d=0):y(a),lx(b),rx(c),val(d){}
}line[manx<<1];
void init()
{
    memset(tree,0,sizeof(tree));
    memset(cover,0,sizeof(cover));
    memset(tree2,0,sizeof(tree2));
}
void eval(int root,int l,int r)
{
    if(cover[root])
        tree[root]=X[r+1]-X[l];
    else if(l==r)
        tree[root]=0;
    else tree[root]=tree[chl]+tree[chr];
    if(cover[root]>=2)
        tree2[root]=X[r+1]-X[l];
    else if(l==r)
        tree2[root]=0;
    else if(cover[root]==1)
        tree2[root]=tree[chl]+tree[chr];
    else
        tree2[root]=tree2[chl]+tree2[chr];
}
void change(int root,int l,int r,int ll,int rr,int val)
{
    if(l==ll&&r==rr)
    {
        cover[root]+=val;
        eval(root,l,r);
        return;
    }
    if(rr<=mid)
        change(chl,l,mid,ll,rr,val);
    else if(ll>mid)
        change(chr,mid+1,r,ll,rr,val);
    else
    {
        change(chl,l,mid,ll,mid,val);
        change(chr,mid+1,r,mid+1,rr,val);
    }
    eval(root,l,r);
}
int main()
{
    int t,n;
    double x1,y1,x2,y2;
    while(scanf("%d",&t)!=EOF)
    {
        while(t--)
        {
            scanf("%d",&n);
            double ans=0;
            init();
            for(int i=1; i<=n; i++)
            {
                scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
                line[i*2]=node{y1,x1,x2,1};
                X[i*2]=x1;
                line[i*2-1]=node{y2,x1,x2,-1};
                X[i*2-1]=x2;
            }
            sort(X+1,X+2*n+1);
            sort(line+1,line+2*n+1);
            int cnt=unique(X+1,X+2*n+1)-X-1;
            //X[cnt+1]=X[cnt];
            for(int i=1; i<2*n; i++)
            {
                int l=lower_bound(X+1,X+cnt+1,line[i].lx)-X;
                int r=lower_bound(X+1,X+cnt+1,line[i].rx)-X-1;
                double dy=line[i+1].y-line[i].y;
                change(1,1,cnt,l,r,line[i].val);
                ans+=tree2[1]*dy;
            }
            printf("%.2f\n",ans);
        }
    }
    return 0;
}

之前还犯的一个数组越界的错，杭电上测出RE了，本来数组开的应该够大。。后面发现是eval函数里面最开始没有排除l== r的情况（即遍历到叶子节点时）导致继续访问叶子结点的“左右儿子”造成tree数组下标越界（因为看学长的模板时还感觉可以不用排除l==r的情况，就没有加）。但数组越界第一次在vj上测得的结果是wa，以前听学长说是因为有野指针。。。所以可能就给tree赋了一个随机数吧