深度学习吴恩达作业题（4）

2、深度神经网络用于图片识别应用

2.1包

dnn_app_utils提供了在此笔记本的“构建深度神经网络：逐步”中实现的功能。
np.random.seed（1）用于使所有随机函数调用保持一致。

import numpy as np
import matplotlib.pyplot as plt
import h5py
def sigmoid(Z):
   A = 1/(1+np.exp(-Z))
    cache = Z   
    return A, cache
def relu(Z):
     A = np.maximum(0,Z)    
    assert(A.shape == Z.shape)    
    cache = Z 
    return A, cache
def relu_backward(dA, cache):
    Z = cache
    dZ = np.array(dA, copy=True) # just converting dz to a correct object.   
    # When z <= 0, you should set dz to 0 as well. 
    dZ[Z <= 0] = 0   
    assert (dZ.shape == Z.shape)   
    return dZ
def sigmoid_backward(dA, cache):
    Z = cache   
    s = 1/(1+np.exp(-Z))
    dZ = dA * s * (1-s)   
    assert (dZ.shape == Z.shape)  
    return dZ
def load_data():
    train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
    test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
    classes = np.array(test_dataset["list_classes"][:]) # the list of classes    
    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))    
    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
def initialize_parameters(n_x, n_h, n_y):
   .random.seed(1)    
    W1 = np.random.randn(n_h, n_x)*0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h)*0.01
    b2 = np.zeros((n_y, 1)) 
    assert(W1.shape == (n_h, n_x))
    assert(b1.shape == (n_h, 1))
    assert(W2.shape == (n_y, n_h))
    assert(b2.shape == (n_y, 1))   
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}   
    return parameters     
def initialize_parameters_deep(layer_dims):
     np.random.seed(1)
    parameters = {}
    L = len(layer_dims)            # number of layers in the network
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) / np.sqrt(layer_dims[l-1]) #*0.01
        parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))      
        assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
        assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))       
    return parameters
def linear_forward(A, W, b):
     Z = W.dot(A) + b    
    assert(Z.shape == (W.shape[0], A.shape[1]))
    cache = (A, W, b)  
    return Z, cache
def linear_activation_forward(A_prev, W, b, activation):
     activation == "sigmoid":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = sigmoid(Z)   
    elif activation == "relu":
        # Inputs: "A_prev, W, b". Outputs: "A, activation_cache".
        Z, linear_cache = linear_forward(A_prev, W, b)
        A, activation_cache = relu(Z)    
    assert (A.shape == (W.shape[0], A_prev.shape[1]))
    cache = (linear_cache, activation_cache)
    return A, cache
def L_model_forward(X, parameters):
    es = []
    A = X
    L = len(parameters) // 2                  # number of layers in the neural network    
    # Implement [LINEAR -> RELU]*(L-1). Add "cache" to the "caches" list.
    for l in range(1, L):
        A_prev = A 
        A, cache = linear_activation_forward(A_prev, parameters['W' + str(l)], parameters['b' + str(l)], activation = "relu")
        caches.append(cache)    
    # Implement LINEAR -> SIGMOID. Add "cache" to the "caches" list.
    AL, cache = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], activation = "sigmoid")
    caches.append(cache)    
    assert(AL.shape == (1,X.shape[1]))           
    return AL, caches
def compute_cost(AL, Y):
      m = Y.shape[1]
    # Compute loss from aL and y.
    cost = (1./m) * (-np.dot(Y,np.log(AL).T) - np.dot(1-Y, np.log(1-AL).T))   
    cost = np.squeeze(cost)      # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
    assert(cost.shape == ())   
    return cost
def linear_backward(dZ, cache):
    rev, W, b = cache
    m = A_prev.shape[1]
    dW = 1./m * np.dot(dZ,A_prev.T)
    db = 1./m * np.sum(dZ, axis = 1, keepdims = True)
    dA_prev = np.dot(W.T,dZ)    
    assert (dA_prev.shape == A_prev.shape)
    assert (dW.shape == W.shape)
    assert (db.shape == b.shape)    
    return dA_prev, dW, db
def linear_activation_backward(dA, cache, activation):
    ar_cache, activation_cache = cache  
    if activation == "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)       
    elif activation == "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache) 
    return dA_prev, dW, db
def L_model_backward(AL, Y, caches):
     {}
    L = len(caches) # the number of layers
    m = AL.shape[1]
    Y = Y.reshape(AL.shape) # after this line, Y is the same shape as AL   
    # Initializing the backpropagation
    dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))   
    # Lth layer (SIGMOID -> LINEAR) gradients. Inputs: "AL, Y, caches". Outputs: "grads["dAL"], grads["dWL"], grads["dbL"]
    current_cache = caches[L-1]
    grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)] = linear_activation_backward(dAL, current_cache, activation = "sigmoid")   
    for l in reversed(range(L-1)):
        # lth layer: (RELU -> LINEAR) gradients.
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads["dA" + str(l + 2)], current_cache, activation = "relu")
        grads["dA" + str(l + 1)] = dA_prev_temp
        grads["dW" + str(l + 1)] = dW_temp
        grads["db" + str(l + 1)] = db_temp
    return grads
def update_parameters(parameters, grads, learning_rate):
    L = len(parameters) // 2 # number of layers in the neural network
    # Update rule for each parameter. Use a for loop.
    for l in range(L):
        parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
        parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]   
    return parameters
def predict(X, y, parameters):
    = X.shape[1]
    n = len(parameters) // 2 # number of layers in the neural network
    p = np.zeros((1,m)) 
    # Forward propagation
    probas, caches = L_model_forward(X, parameters) 
    # convert probas to 0/1 predictions
    for i in range(0, probas.shape[1]):
        if probas[0,i] > 0.5:
            p[0,i] = 1
        else:
            p[0,i] = 0  
    #print results
    #print ("predictions: " + str(p))
    #print ("true labels: " + str(y))
    print("Accuracy: "  + str(np.sum((p == y)/m)))       
    return p
def print_mislabeled_images(classes, X, y, p):
     a = p + y
    mislabeled_indices = np.asarray(np.where(a == 1))
    plt.rcParams['figure.figsize'] = (40.0, 40.0) # set default size of plots
    num_images = len(mislabeled_indices[0])
    for i in range(num_images):
        index = mislabeled_indices[1][i]       
        plt.subplot(2, num_images, i + 1)
        plt.imshow(X[:,index].reshape(64,64,3), interpolation='nearest')
        plt.axis('off')
        plt.title("Prediction: " + classes[int(p[0,index])].decode("utf-8") + " \n Class: " + classes[y[0,index]].decode("utf-8")

2.2数据集

您将使用与“逻辑回归作为神经网络”（分配2）中相同的“猫与非猫”数据集。 您建立的模型在对猫和非猫图像进行分类时具有70％的测试准确性。 希望您的新模型性能更好！
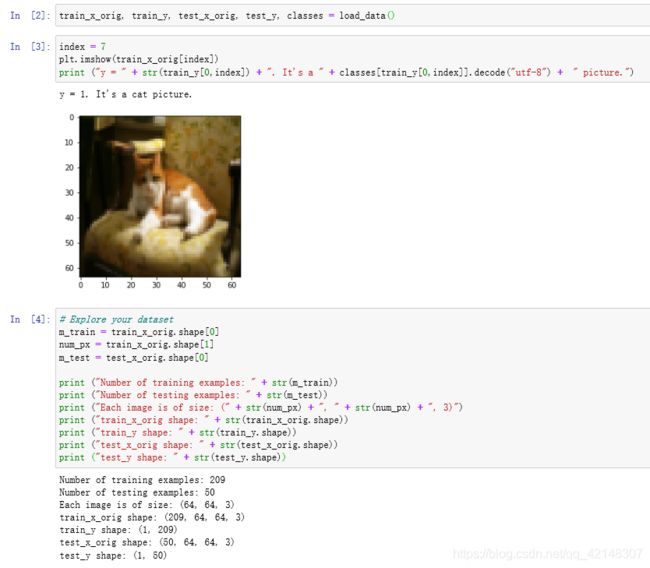
问题陈述：您将获得一个包含以下内容的数据集（“ data.h5”）：
-标记为cat（1）或非cat（0）的m_train图像的训练集
-标记为cat和non-cat的m_test图像的测试集
-每个图像的形状（num_px，num_px，3），其中3表示3个通道（RGB）。

2.3构建你的模型

与往常一样，您将遵循深度学习方法来构建模型：
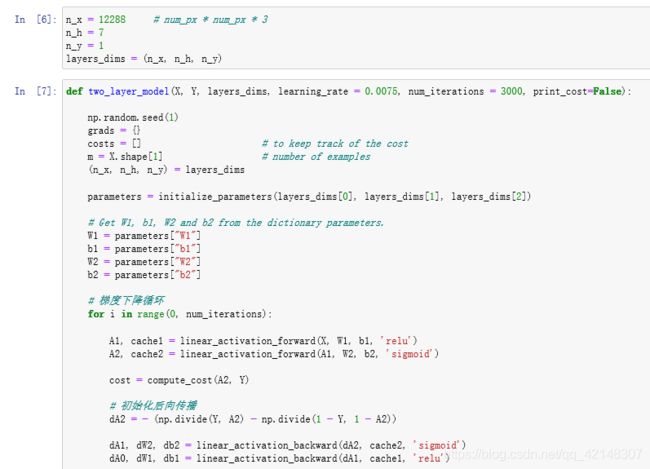
1.初始化参数/定义超参数
2.循环执行num_iterations：
正向传播
计算成本函数
向后传播
更新参数（使用参数和反向传播的渐变）
4.使用训练有素的参数来预测标签

2.4两层神经网络

2.5L层神经网络

2.6测试自己的图片