强化学习笔记+代码（六）：Policy Gradient结构原理和Agent实现(tensorflow)

本文主要整理和参考了李宏毅的强化学习系列课程和莫烦python的强化学习教程
本系列主要分几个部分进行介绍

1. 强化学习背景介绍
2. SARSA算法原理和Agent实现
3. Q-learning算法原理和Agent实现
4. DQN算法原理和Agent实现(tensorflow)
5. Double-DQN、Dueling DQN算法原理和Agent实现(tensorflow)
6. Policy Gradients算法原理和Agent实现(tensorflow)
7. Actor-Critic、A2C、A3C算法原理和Agent实现(tensorflow)

一、Policy Gradient

之前说的SARSA、Q-learning、DQN学习的都是在状态s下动作a的价值，属于value-based的方法。而Policy Gradient学习的是在状态s下每个动作a被选择的概率，属于policy-based的方法。

我们先说Policy Gradient的整体思想，之后将整体思想进行拆分，产生Policy Gradient每一步的流程。

Policy Gradient的网络要学习的是状态下动作输出的概率。按照常识来讲，可以获得越大的奖励的动作应该被选择的概率是越大的。需要注意的是这里所说的奖励并不是一个动作单步的奖励，而是当整个游戏结束时，这个动作整体所产生的价值，这个价值我们叫做advantage。因此我们的网络要学习的目标就是：按照每个动作的概率进行选择时，获得的奖励的期望值是最大的。

于是，我们有一个大致的Policy Gradient学习流程：先根据初始状态产生选择动作和到达的新状态，如此往复知道终点，我们可以得到一系列的状态和动作$(s_1,a_1),(s_2,a_2)...(s_n,a_n)$。由于每个动作$a_i$获得的奖励是知道的，因此我们我们可以获这个动作的advantage。于是我们可以训练我们的网络参数$\theta$，使网络的输出（即每个动作被选择概率）获得的奖励的期望值最大。

设我们有初始参数为$\theta$的网络，可知出现行动状态序列 $\tau$似于一阶马尔科夫过程，其概率为:

由于环境是给定不可以改变的，所以公式中只有$p_{\theta }(a_t|s_t)$与参数$\theta$有关。进一步还可以得到在此参数下网络获得奖励期望：

目标是奖励的期望的值最大，因此我们的重点是求出期望的梯度，并根据梯度的方向不断更新。原始的policy gradient算法如下：

上面算法图中的红框的部分就是期望的梯度，其中$v_t$是序列$\tau$的价值，即之前说的$R(\tau )$.
那么我们如何求期望的梯度呢？

由于$R(\tau )$与$\theta$是无关的。因此我们有：

又因为

所以我们可以得到期望的梯度的求解如下：

对于期望求梯度其实只需要对$log{p}_{\theta }()$求梯度（即神经网络的输出，普通神经网络的更新我们是熟悉的），于是我们可以通过所以sample出N个$\tau$ ，对每个$\tau$求 $R({\tau }^n)\nabla log{p}_{\theta }({\tau }^n)$ 再求和取平均。
具体的更新过程如下图：

我们根据网络产生需要序列$\tau$，利用$\tau$对网络进行训练。训完后后用最新的网络参数继续产生序列$\tau$，再对网络进行训练。如此往复即可达到强化学习的目的。

二、Policy Gradient的一些技巧

在使用Policy Gradient时我们可以使用一些技巧，是网络更加有效或者更快的学习。

1. 添加基准线b
   由于训练过程中采样是随机的，可能会出现某个行动不被采样的情况，这会导致采取该行动的概率下降；另外，由于采取的行动概率和为一，可能存在归一化之后，好的action的概率相对下降，坏的action概率相对上升的情况，因此需要引入一个基准线.
   
   添加基准线的方式十分简单，利用如下公式即可
   

2. 全局收益->累计收益
   
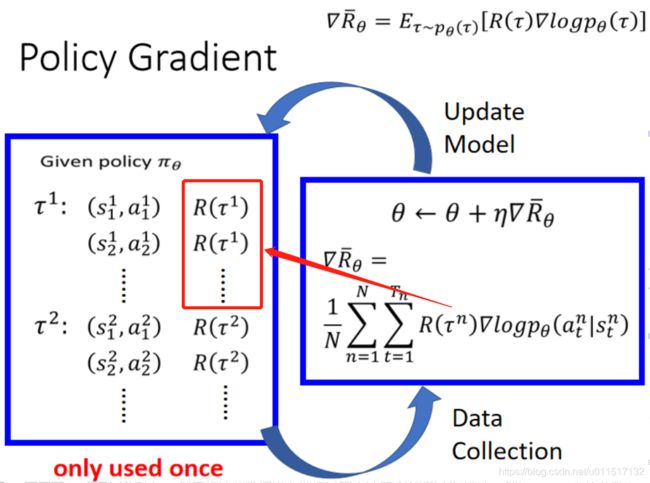
   由上图的学习方式中可以看到，不管其中的某个action是好是坏，都会乘上整个序列的奖励$R(\tau )$，这显然也是不公平的。如果我们的训练样本跟大，这种不公平性可能形象不大（但是学习可能会放缓），但是训练样本少的时候，影响就比较大了。因此我们将$R(\tau )$进行替换成语时间和动作有关的因子，即使用如下方式：
   
   其中t代表该动作执行的时刻，即把当前的 $r_{t^{\prime }}$为执行动作后每一步的奖励，$\gamma$为奖励传递的衰减系数

3. on-policy->off-policy
   有上面的流程可知，每次训练Policy Gradient都要用最新的网络与环境进行交互产生新的训练样本。交互过程无疑是浪费时间的。我们可以仿照DQN建立target network的思想。用一个较老的网络产生的样本重复使用，对网络进行训练。只是期望的梯度会发生变化，具体推导如下：
   
   
   
   
   除了上面这些技巧外，还有许多其他对网络训练的改进，比如在原来加入分布差异惩罚的PPO等方法。

二、Policy Gradient的Agent实现

此处使用加入基准线b,并且使用累积收益计算方式的Policy Gradient结构进行Agent编写

from maze_env_drl import Maze
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt

class PolicyGradient(object):
    
    def __init__(self, n_actions, n_features, learning_rate=0.01, reward_decay=0.95, output_graph=False):
        self.n_actions = n_actions
        self.n_features = n_features
        self.lr = learning_rate     # 学习率
        self.gamma = reward_decay   # reward 递减率
        
        #因为需要模拟整个回合才能得到最终奖励，才能进行网络学习，所以需要将达到终点点整个序列的状态、动作、奖励记录下来
        self.ep_obs, self.ep_as, self.ep_rs = [], [], []    #这是我们存储 回合信息的 list
        
        #下面与之前是一样的
        self._build_net()  #建立网络
        self.sess = tf.Session()
        
        if output_graph:
            tf.summary.FileWriter("logs/", self.sess.graph)
        
        self.sess.run(tf.global_variables_initializer())
        
    #与此前不同之前储存记忆利用的是replay buffer机制。存储内容分可能来自不同执行序列和不同参数的神经网络
    #此处只是为了储存达到终点前一个系列的动作
    def store_transition(self, s, a, r):
        self.ep_obs.append(s)
        self.ep_as.append(a)
        self.ep_rs.append(r)
    
    #构建网络，因为直接走到终点，奖励是可以观察的，不再需要target_work去求st+1的最大价值
    def _build_net(self):
        tf.reset_default_graph()  #清空计算图
        with tf.name_scope('input'):
            self.tf_obs = tf.placeholder(tf.float32, [None, self.n_features], name="observations")  #接收observation
            #标签维度为[batch_size, 1]。标签是具体动作，不是概率
            self.tf_acts = tf.placeholder(tf.int32, [None, ], name="actions_num")   # 接收我们在这个回合中选过的actions
            #接收每个state-action所对应的value(通过reward计算),注意此处不是单步的奖励，而是整个一些列动作的奖励,vt=本reward + 衰减的未来reward
            self.tf_vt = tf.placeholder(tf.float32, [None, ], name="actions_value")
        
        #权重初始化方式
        w_initializer = tf.random_normal_initializer(0.,0.3)  
        b_initializer = tf.constant_initializer(0.1)
        n_l1 = 10  #n_l1为network隐藏层神经元的个数 
        with tf.variable_scope("lay1"):
            w1 = tf.get_variable('w1', [self.n_features, n_l1], initializer=w_initializer)
            b1 = tf.get_variable('b1', [1, n_l1], initializer=b_initializer)
            l1 = tf.nn.tanh(tf.matmul(self.tf_obs, w1)+b1)
        with tf.variable_scope("lay2"):
            w2 = tf.get_variable('w2', [n_l1, self.n_actions], initializer=w_initializer)
            b2 = tf.get_variable('b2', [1, self.n_actions], initializer=b_initializer)
            output = tf.matmul(l1, w2)+b2
        
        #ploicy gradient求解在一个状态下每个动作的概率，因此使用softmax出动作概率
        self.all_act_prob = tf.nn.softmax(output)
        
        with tf.name_scope('loss'):
            #交叉熵作为损失函数,训练样本中选中的action即为我们的label,因为还没求出最终损失,此处用reduce_sum
            neg_log_prob = -tf.reduce_sum(tf.log(self.all_act_prob)*tf.one_hot(self.tf_acts, self.n_actions), axis=1)
            #可是视为当前这个局部损失*对应权重，可以看到state-action的value越大，权重越大
            #可以认为state-action的value越大，就越会顺着这个梯度下降，这个动作就越可信
            #若不加基准线b为如下方式：
            #loss = tf.reduce_mean(neg_log_prob * (self.tf_vt))
            
            #加入基准线b的损失
            loss = tf.reduce_mean(neg_log_prob * (self.tf_vt-tf.reduce_mean(self.tf_vt)))
            
        with tf.name_scope('train'):
            self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)
    
    #之前DQN根据最大动作价值选择动作，ploicy gradient根据网络输出的动作概率，依照概率选择动作
    def choose_action(self, observation):
        # 所有action的概率
        prob_weights = self.sess.run(self.all_act_prob, feed_dict={self.tf_obs: observation[np.newaxis, :]})
        #按照概率选择动作
        action = np.random.choice(range(prob_weights.shape[1]), p=prob_weights.ravel())
        return action
    
    #用于计算回合的state-action value
    def _discount_and_norm_rewards(self):
        #先计算单步的奖励，在逐步将后面的奖励逐步衰减加到前面
        discounted_ep_rs = np.zeros_like(self.ep_rs)
        running_add = 0
        
        #将后面的奖励逐步衰减加到前面
        for t in reversed(range(len(self.ep_rs))):
            running_add = running_add * self.gamma + self.ep_rs[t]
            discounted_ep_rs[t] = running_add
            
        #防止每个回合计算出的奖励量纲不同，进行正态标准化
        discounted_ep_rs = np.array(discounted_ep_rs,dtype=np.float) 
        discounted_ep_rs -= np.mean(discounted_ep_rs)
        discounted_ep_rs /= np.std(discounted_ep_rs)
        
        return discounted_ep_rs
    
    def learn(self):
        #因为训练时传入的不是动作单步奖励，执行完动作后的整体奖励，因此先计算执行完动作后的整体奖励
        discounted_ep_rs_norm = self._discount_and_norm_rewards()
        #np.vstack(self.ep_obs)的shape=[None, n_obs]，np.array(self.ep_as)的shape=[None,]，discounted_ep_rs_norm的shape=[None,]
        #每次的训练样本相当于一和完整流程状态和对应的动作以及对应奖励。
        self.sess.run(self.train_op, feed_dict={self.tf_obs: np.vstack(self.ep_obs),self.tf_acts: np.array(self.ep_as),self.tf_vt: discounted_ep_rs_norm})
        #次回合动作已经训练完，清空记忆。下次训练需要重新产生训练样本
        self.ep_obs, self.ep_as, self.ep_rs = [], [], []
        
        #返回这一回合的state-action value
        return discounted_ep_rs_norm  

def run_maze(RENDER):
    for episode in range(3000):
        # 初始化环境
        observation = env.reset()
        while True:
            if RENDER:
                # 刷新环境
                env.render()
            # DQN 根据观测值选择行为
            action = RL.choose_action(observation)
            # 环境根据行为给出下一个state, reward,是否终止
            observation_, reward, done = env.step(action)
            #存储记忆
            RL.store_transition(observation, action, reward)
            #知道获得最终奖励才能进行训练，这是MC的方法
            if done:
                ep_rs_sum=sum(RL.ep_rs)
                
                if 'running_reward' not in locals():
                    running_reward = ep_rs_sum
                else:
                    running_reward = running_reward * 0.99 + ep_rs_sum * 0.01
                
                if running_reward> DISPLAY_REWARD_THRESHOLD:
                    RENDER=True
                
                print("episode:", episode, "  reward:", int(running_reward))
                
                vt = RL.learn()
                
                if episode==0:
                    plt.plot(vt)    # plot这个回合的vt
                    plt.xlabel('episode steps')
                    plt.ylabel('normalized state-action value')
                    plt.show()
                break   #此次模拟完毕
                
            observation = observation_  #还没有获取奖励，去要继续执行模拟

if __name__=="__main__":
    RENDER=False
    DISPLAY_REWARD_THRESHOLD=300
    env = Maze() 
    
    RL = PolicyGradient(n_actions=env.n_actions, n_features=env.n_features, learning_rate=0.02, reward_decay=0.99, output_graph=True)
    run_maze(RENDER)