【前言】在很多计数问题中,常常要把所有计数的对象分成若干个不重复又不遗漏的类型,使得每类便于计数。但是实际的问题却往往较为复杂,而且容易混为一团,难以区分,而要准确无误的计算事物的个数,就得运用容斥原理,这类问题往往被称为重叠问题,也叫包含与排除问题。徐长青老师对能力的理解是:能用学过的知识,成功地解决陌生的问题。在课程中,与孩子们一起对重叠问题进行了探究和进一步拓展。并建构起数学与语文关联词“既……又……”的关系,还进一步利用手势反复建立和沟通已有认知和未知的联系,从而将头脑中已有的模糊感知转化成数学中的图形表达。做到了,会看,会说,会表达。
一、故事引入
1)故事导入
理发店来了客人,客人说:“叔叔,我和爸爸要剃头”,又来了客人,说:“师傅,给我和我父亲剃个头”。这时,理发店抬起头一看,很纳闷。
师:“你们猜猜理发师为什么纳闷呢?”
生:“因为两句话里本来应该有4个人,可是他看到的却只有三个人。”
2)初步感知重复问题
师:“那是哪三个人呢?”
生:“一个儿子和他的爸爸,还有一个是爷爷”
(引入手势嚓嚓嚓)
顺势问:“4个手指,怎么变成3个手指?”
生:“把两个手指叠在一起。”“为什么?”
生:“爸爸是儿子的爸爸,爸爸是爷爷的儿子。这样就只有三个人了”
引出关联词“既……又……”
(重复手势 嚓嚓嚓,将语文关联词与肢体语言结合起来)
二、游戏
1)抢椅子游戏
找两把椅子,再喊2个孩子上来。
师:“人都到了,为什么还有人举手?
生:“人和椅子一样多,一一对应,因此无法淘汰,需要加人。”
又有请4人。
生:“人太多了,只要3个人”。
师:“那现在怎么办?”
生:“减人”。
2)请后来上来的4名同学进行石头剪刀布(公平游戏),1人闯关晋级,淘汰3人。
三、深度体验
1)说明游戏规则
顺时针跑,听到停就抢板凳坐下,不坐腿,后坐下的淘汰。两轮游戏后,剩一名女生晋级冠军。
2)采访冠军
贯穿德育,引导女生感谢所有参与游戏的同伴,才有冠军的诞生。
3)请参与游戏的孩子们领荣誉
师:“站起来6个人,怎么少人了?面对荣誉不要推让。”
生:“猜拳的和抢椅子的都到了,裁判扮演了两个角色,所以看起来好像少了,但是所有人都到了。”
师:“那我们来算一算,猜拳的几个人?抢椅子的几个人?”
生:“4+3”
师:“等于7!还差一个人,请站起来。”
生:“6个人!”
师:“7个人!”
(通过师生对抗,引起认知冲突,体验新知)
4)呼啦圈套人
用一个呼啦圈代表抢椅子的3个人,一个呼啦圈代表猜拳的4个人,请孩子们入圈。
师:“还有一个人呢?"
(此时有个孩子不知所措,不知道该站哪边。)
师:“用事实说话,如果能让一个圈里有3个人,一个圈里有4个人,你们就赢了。”
(老师退场,越走越远。使孩子们减少对老师的依赖心理,自己想解决方案。学生茫然,经过一阵对峙,孩子们想到将两个呼啦圈组合到一起。然后让学生分别数数现在两个圈里的人数,已然满足3人和4人。,但是总共才6人。)
师:“我今天终于承认4+3=6”。
生:“不对!***既参加猜拳,又参加抢椅子,两个圈里都有他,其实是有2个他,但是我们只要一个他,所以要减去1。4+3-1=6”。
师:“那减去的1是谁?”
生:“***”
师:“那***先走得远一些,我们再数一数。出事了!减了1变成5了,看来减的1不是他,那减的1是谁呢?”
生:“我们先把两个他都算进去,再减去第一个多余的他,留下一个角色还给他。”
师:“如果他玩了3个游戏,要减去几个他?8个游戏?100个游戏呢?”
生:“2个,7个,99个”。
师:“也就是说,要留下一个角色给他,使得一一对应。这就是数学中的两环”。
(重复手势 嚓嚓嚓)
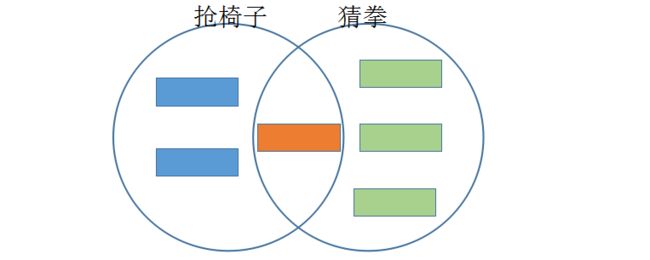
5)画图
师:“图应该怎么画?”
生:“要有一部分重叠”。
(此时学生在手势的结合下,已经能感知出不重复、完全重复和不完全重复的画法。)
师:“那这就是既……又……”。
6)贴名字条
抢椅子的3人贴完之后,师整理名字条,学生大呼“不要”。
(建立孩子们头脑中关于“既……又……”的关系图模型)
再请猜拳的4人上来贴名字条,那个“既……又……”的同学又贴了一次,紧接着他又拿走了自己名字条。
师:“为什么这个同学又拿走了自己的名字条?”
生:“因为第一次他已经贴过了,那个位置就是他的了,就不用再多贴一次了。”
师:“现在请***挑战一下,把你的两张名条都贴上。”
学生们纷纷出主意,让他把名条重叠在一起贴,有的用语言,有的用肢体示范,特别着急。
(现在孩子们对这样重复的量已经有更深层次的感觉了)
师:“所以在玩游戏时,需要一分为二,计算人数时,要合二为一。因为我们班只有一个***,应该减去他多余的角色,回到一一对应。”
(重复手势 嚓嚓嚓)
四、问题解决,运用新知
出示例题:三年级一班有女生19人,男生17人,全班多少人?
生:“19+17=36(人)”
师:“今天学的是重复,都要减去,你们怎么不减呢?”
生:“因为女生和男生是不一样的,不是同一类人,没有重复,所以男生加女生就是全部的人。”
师:“所以学过的不能用来解决所有的问题,数学要注意运用的环境、条件、规则。”
(教孩子们活用知识,而不是生硬地套用思维定势去解决问题。)
五、回归情景,拓展新知
小调查:爸爸抽烟、喝酒的情况(重复手势 嚓嚓嚓)
既吸烟又喝酒的孩子站起来。只吸烟不喝酒的孩子起立。只喝酒不吸烟的孩子站起来。
师:“13+17=30,是我们全部的同学吗?还有谁没站起来?”
生:“因为我爸爸既不抽烟,也不喝酒。”
师:“那这样的爸爸往哪儿放呢?”
生:“在外面加个长方形,把好爸爸放在韦恩图外面,长方形里面。”
师:“我们希望圈里的爸爸早点跳出来,做个好爸爸。”
(拓展了孩子们对集合的初步感知,为以后更高段的学习做些铺垫)
本节课的收获:
1)本节课学习了基本的重叠问题时,延伸了些关于集合方面的知识,实际上在初中的学习中也有很多与重复有关的知识,比如线段,角的重叠问题,在三角形全等的证明,求重复部分的面积,镶嵌等问题,都要遵循不重不漏的原则。因此本节课的内容对之后很多内容的学习都起到了举足轻重的作用。
2)为了让孩子们能顿悟重复的量,并且学会如何处理重复的量,徐老师设计的每一个环节层层递进,在游戏化学习中,让孩子们亲身体验,让孩子们在老师的追问中不断地反驳,构建自己的认知,由自己寻求答案,成功地掌握方法,并自行解决问题。在一个又一个游戏,一个又一个冲突的引领下,孩子们乐在其中,又在不知不觉中留下深刻印象。这样诙谐幽默,又贯穿着德育的课堂,都是我们也可以学着渗透进自己的教学中的精华。