OPENAI-Baeslines-详解(二)-DQN中文
Zee带你看代码系列
学习强化学习,码代码的能力必须要出众,要快速入门强化学习 搞清楚其中真正的原理,读源码是一个最简单的最直接的方式。最近创建了一系列该类型文章,希望对大家有多帮助。
传送门
另外,我会将所有的文章及所做的一些简单项目,放在我的个人网页上。
水平有限,可能有理解不到位的地方,希望大家主动沟通交流。
邮箱:[email protected]
Thanks for reading, and enjoy yourself
DQN
2013年,DQN算法被提出,奠定了深度学习与强化学习相结合的基础,此后各种DRL算法层出不穷。作为旷世之作,各种文章分析已经非常多,包括其变种算法:dueling DQN、Double DQN、continuous DQN。
比较推荐的2个教程:
莫凡周的DQN教程
CSDN的DQN博客
算法部分
Q Learing算法
Q_learning算法是值函数的经典算法之一,其利用估计动作值函数,然后选择最好的动作。该算法利用时序差分的方式来更新Q值函数:
DQN算法
DQN算法 利用神经网络去拟合Q函数,面临3个问题:RL样本不独立、RL分布变化、RL样本没标签。
主要靠2个Trick:
1、经验回放:从经验池中挑选出使得 RL样本 互相无关,并且可以学总体概率分布。
2、标签构造-传统训练神经网络的时候是一个监督学习过程,需要标签,DQN将标签构造为
R t + 1 + γ max a Q ( S t + 1 , a ) R_{t+1}+\gamma \max _{a} Q\left(S_{t+1}, a\right) Rt+1+γamaxQ(St+1,a)
利用一个网络main-net 去计算当前的 Q ( S t , a ) Q\left(S_{t}, a\right) Q(St,a) 用另一个网络target-net 去计算 Q ( S t + 1 , a ) Q\left(S_{t+1}, a\right) Q(St+1,a). 这样就可以得到神经网络的训练误差LOSS:
Q ( S t , a ) − ( R t + 1 + γ max a Q ( S t + 1 , a ) ) Q\left(S_{t}, a\right)-(R_{t+1}+\gamma \max _{a} Q\left(S_{t+1}, a\right)) Q(St,a)−(Rt+1+γamaxQ(St+1,a))
利用该误差去更新网络参数,最后求得准确的Q值。
target-net的更新都是利用mainnet的参数,更新方式有两种,一种是软更新,即:
Var_tar = ( 1 − α ) (1-\alpha) (1−α) Var_tar + α \alpha α Var_main
一种是硬更新,即在多少次迭代之后将Var_main 直接赋值给 Var_tar。
其中Var_tar 为target_net 的参数, Var_main为main_net的参数。
double DQN
double DQN 是为了解决神经网络过拟合的问题。
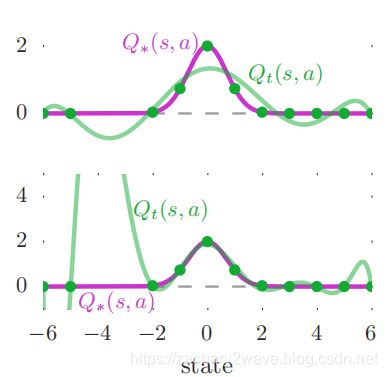
引用原论文中的例子,来简单说明一下过拟合。首先有一个函数 Q ∗ ( S t , a ) = 2 e x p ( − s 2 ) Q_*\left(S_{t}, a\right)=2exp(-s^2) Q∗(St,a)=2exp(−s2),我们通过与环境交互得到了一些状态和动作,假设我们已经知道这些Q值都是正确的Q值。 那么利用现在采样的数据去拟合Q函数,然后才可以得到其他状态下的Q值函数。如果尝试用分别用6阶多项式和9阶来进行拟合的时候,上图为6阶拟合 明显看出这里没有拟合好,下图为9阶拟合,可以看出过拟合的情况。
其实,神经网络是具有非线性激活函数的多项式。那么可以想到,面对一个环境是寻找一个合适的神经网络也是非常困难的。
所以针对这个问题,2015年 Deep Mind 的Hado van Hasselt 等几个人在 文章提出了double DQN网络。具体实现就是在选择 Q ( S t + 1 , a ) Q\left(S_{t+1}, a\right) Q(St+1,a)的时候不在利用target net动作a 而是利用main net 的动作a。这样很大程度上避免了 每次都选择最大的Q值动作。
更深层次的原理,请移步深度解读系列。
Y t Double Q ≡ R t + 1 + γ Q ( S t + 1 , argmax a Q ( S t + 1 , a ; θ t ) ; θ t ′ ) Y_{t}^{\text {Double } Q} \equiv R_{t+1}+\gamma Q\left(S_{t+1}, \underset{a}{\operatorname{argmax}} Q\left(S_{t+1}, a ; \boldsymbol{\theta}_{t}\right) ; \boldsymbol{\theta}_{t}^{\prime}\right) YtDouble Q≡Rt+1+γQ(St+1,aargmaxQ(St+1,a;θt);θt′)
Dueling DQN
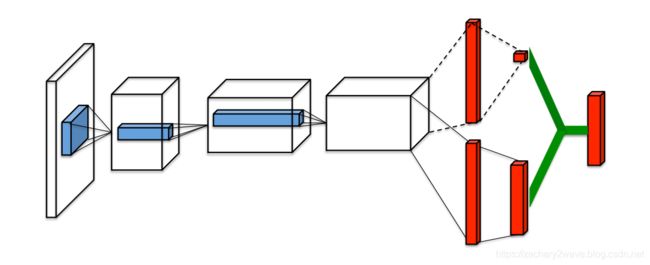
2016年Deep Mind 在此基础上又提出了 Dueling DQN,Dueling DQN的主要思路是在实际的环境中,没有必要估计每个操作Q值。所以Dueling DQN用一种更为直接的方式去解决了这个问题,就是用同一个网络的做多输出的状态,其中上面一个输出口作为状态的V值输出, 下面的输出口作为每一个动作的Q值输出。
Q ( s , a ; θ , α , β ) = V ( s ; θ , β ) + A ( s , a ; θ , α ) Q(s, a ; \theta, \alpha, \beta)=V(s ; \theta, \beta)+A(s, a ; \theta, \alpha) Q(s,a;θ,α,β)=V(s;θ,β)+A(s,a;θ,α)
上面的 θ \theta θ代表的是前面层网络的输出, α \alpha α β \beta β 分别是输出V值和A值的全连接网络层。
调用DQN
在OPENAI-Baeslines-详解(一)中已经有说明,这里具体说一下 DQN与其他的调用的不同。
参数方便,DQN有一些特殊的超参数,需要调整。
普通参数:
env, # 所要训练的环境 一般为env=gym.make('envID')
network, # 字符串 'mlp'等几个 ,或者自己建立的网络。
seed=None, # 随机种子
total_timesteps=100000, # 总训练步数
train_freq=1, # 总训练的频率,也就是每隔几步一训练
print_freq=100, # 在运行中多少步 输出一次训练结果
**network_kwargs # 网络构建参数
checkpoint_freq=10000, # 多少步保存一次网络参数
checkpoint_path=None, #
param_noise=False, # 参数噪声
callback=None, # 调用的callback
load_path=None, # 调用
算法超参数
lr=5e-4 # 学习率
exploration_fraction=0.1, # 探索退火率
exploration_final_eps=0.02, # 探索最小值
learning_starts=1000, # 从什么步数开始学习
gamma=1.0, # 公式(1)中的参数gamma
target_network_update_freq=500, # 硬更新的时候多少步更新一次
经验池参数
包含优先经验回放 (参考文章)[https://arxiv.org/abs/1511.05952]
batch_size=32, # 每次选用的batch 是多大
buffer_size=50000, # 训练池大小
prioritized_replay=False, # 优先经验回放
prioritized_replay_alpha=0.6,
prioritized_replay_beta0=0.4,
prioritized_replay_beta_iters=None,
prioritized_replay_eps=1e-6,
训练参数
除了上面呢些 还有一些 需要在deep单独的参数需要设定。 分别在下面程序部分进行说明。
DQN程序部分
DQN的程序主要是有以下几个部分:
-
Deepq: 主程序, 创建与环境交互循环,调用build_graph创建训练器 和
-
build_graph:由于策略固定,所以只需要DQN只包含一个神经网络用于估计Q值,然后直接输出动作,所以整个过程只需要一个actor 输入为 状态 输出为动作。根据这个过程需要创建几个函数不同的函数
- 总函数 build_train
- 子函数 build_act 创建不带噪声的动作
- 子函数 build_act_with_param_noise 创建带噪的动作
-
Models: 创建神经网络模型
-
replay_buffer: 经验池
整个流程是这样的的
一、Run 调用Deepq中的 learning 建立agent。
-
Learning 调用 deepq.model 建立神经网络 。
- deepq.model根据 common中models建立 神经网络的输入层和隐层,
- 利用 build_q_function 函数 建立输出层(这里可以增加duelingDQN)从而形成完整的神经网络。
-
利用build_grapgh 中的build_act函数建立 状态 到 action的映射函数actor,在这里将确定性的动作选择 变为 随机动作
-
反向传播的trainer ,在这里增加正则化和 double DQN
二、利用建立好的agent 进行训练(在learning内部)
三、测试
附:tf_util.function说明
function(inputs, outputs, updates=None, givens=None)
input、output都是tf.tensor updates是在输入input 之后 直接计算出 output 后 利用update提供的 loss 反向传播 更新 神经网络参数。
Deepq
193行 ,进行步骤一
202行, 调用子程序build_graph 建立agent
Models-build_q_func
network # 网络模型
hiddens=[32] # 隐层
dueling=True, # 是否利用dueling DQN
layer_norm=False # 隐层normalize
**network_kwargs # 其他网络参数
### deepq-learner
输入 :
make_obs_ph : 状态名称 用于创建 placeholder
q_func: Q函数的神经网络
num_actions: 状态数
optimizer : 优化器
grad_norm_clipping: 梯度剪裁
gamma: 公式1 中的 gamma
double_q: 是否利用 double Q算法
param_noise: 参数噪声
输出 :
act_f #动作输出函数
train #训练函数
update_target # target 更新函数
##### 正向传播 act_f 函数
act_f 函数 直接调用子函数 build_act 或者 build_act_with_param_noise 生成
```python
# 创建placeholder
# 177~183行in build_act 239 ~ 243 行 in build_act_with_param_noise
observations_ph = make_obs_ph("observation")
stochastic_ph = tf.placeholder(tf.bool, (), name="stochastic")
update_eps_ph = tf.placeholder(tf.float32, (), name="update_eps")
# 创建神经网络
q_values = q_func(observations_ph.get(), num_actions, scope="q_func")
# 选择动作 184行 in build_act 294行 in build_act
deterministic_actions = tf.argmax(q_values, axis=1) # 确定性动作
random_actions = tf.random_uniform(tf.stack([batch_size]), minval=0, maxval=num_actions, dtype=tf.int64)
chose_random = tf.random_uniform(tf.stack([batch_size]), minval=0, maxval=1, dtype=tf.float32) < eps
stochastic_actions = tf.where(chose_random, random_actions, deterministic_actions) # 随机性动作
# 网络更新 191 行 in build_act 301行 in build_act
output_actions = tf.cond(stochastic_ph, lambda: stochastic_actions, lambda: deterministic_actions)
update_eps_expr = eps.assign(tf.cond(update_eps_ph >= 0, lambda: update_eps_ph, lambda: eps))
# 利用function 更新 193 行 in build_act 308行 in build_act
_act = U.function(inputs=[observations_ph, stochastic_ph, update_eps_ph],
outputs=output_actions,
givens={update_eps_ph: -1.0, stochastic_ph: True},
updates=[update_eps_expr])
反向传播-train 函数
# 估计当前Q值
q_t = q_func(obs_t_input.get(), num_actions, scope="q_func", reuse=True) # reuse parameters from act
q_func_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope=tf.get_variable_scope().name + "/q_func")
# 估计目标Q值
q_tp1 = q_func(obs_tp1_input.get(), num_actions, scope="target_q_func")
target_q_func_vars = tf.get_collection(tf.GraphKeys.GLOBAL_VARIABLES, scope=tf.get_variable_scope().name + "/target_q_func")
q_t_selected = tf.reduce_sum(q_t * tf.one_hot(act_t_ph, num_actions), 1)
q_tp1_best = tf.reduce_max(q_tp1, 1)
q_tp1_best_masked = (1.0 - done_mask_ph) * q_tp1_best
# 公式 1
q_t_selected_target = rew_t_ph + gamma * q_tp1_best_masked
# LOSS 公式2
td_error = q_t_selected - tf.stop_gradient(q_t_selected_target)
# 创建 train
train = U.function(inputs=[
obs_t_input,
act_t_ph,
rew_t_ph,
obs_tp1_input,
done_mask_ph,
importance_weights_ph
],
outputs=td_error,
updates=[optimize_expr]
)
update_target = U.function([], [], updates=[update_target_expr])
q_values = U.function([obs_t_input], q_t)
DQN结果部分
在最后 会得到的文件中会记录 3个部分
| % time spent exploring | 80 |
| episodes | 100 |
| mean 100 episode reward | -200 |
| steps | 1.98e+04 |
分别代表多少个回合 平均 奖励 和总步数。