Neural Network Dynamics for Model-Based Deep Reinforcement Learning with Model-Free Fine-Tuning
文献目录
本文的思想较为简单,简而言之可分为以下四步:
- 首先通过智能体执行随机策略获取一定数量的样本用于建立动力学模型;
- 然后使用传统控制方法依托所学习的动力学模型进行规划,并得到专家轨迹;
- 使用模仿学习从专家轨迹中学习出一个参数化策略;
- 将学习得到的参数化策略作为无模型强化学习算法的起始策略。
文章目录
- 1. INTRODUCTION
- 2. PRELIMINARIES
- 3. MODEL-BASED DEEP REINFORCEMENT LEARNING
- A. Neural Network Dynamics Function
- B. Training the Learned Dynamics Function
- C. Model-Based Control
- D. Improving Model-Based Control with Reinforcement Learning
- 4. MB-MF: MODEL-BASED INITIALIZATION OF MODEL-FREE REINFORCEMENT LEARNING ALGORITHM
- A. Initializing the Model-Free Learner
- B. Model-Free Reinforcement Learning
- 5. EXPERIMENTAL RESULTS
- 6. DISCUSSION
1. INTRODUCTION
- Model-free方法具有很高的样本复杂度,而model-based方法要更有效率;
- 现有的model-based算法通常要么使用简单的函数逼近器,要么使用抗过拟合的贝叶斯模型,以便有效地使用较少的样本学习动态。这使得它们很难应用于范围广泛的复杂、高维的任务;
- 现有的使用大型、富有表现力的神经网络的model-based方法通常表现并不是很好,局限于相对简单的、低维的任务;
- 由于模型偏差,model-based方法的渐近性能通常比model-free方法差。model-free算法不受模型精度的限制,因此可以获得更好的最终性能,但代价是样本复杂度更高。
为解决上述问题,作者将神经网络与模型预测控制(MPC)相结合,提出一种高效的适用于解决高维、富接触问题的model-based算法,其中模型使用深度神经网络搭建,此外还提出了一种使用model-based学习器初始化model-free学习器以实现高回报并大幅降低样本复杂性的方法。
2. PRELIMINARIES
每一时间步的目标是采取最大化未来奖励的折扣总和的动作,由 ∑ t ′ = t ∞ γ t ′ − t r ( s t ′ , a t ′ ) \sum_{t'=t}^{\infty}\gamma^{t'-t}r(s_{t'},a_{t'}) ∑t′=t∞γt′−tr(st′,at′)给出,其中 γ ∈ [ 0 , 1 ] \gamma\in[0,1] γ∈[0,1]是优先考虑近期奖励的折扣因子。执行策略需要了解基础奖励函数 r ( s t , a t ) r(s_t,a_t) r(st,at)或从样本中估计奖励函数(IRL)。在这项工作中,我们假设已知基础奖励函数,在已学习的模型下我们将其用于规划行为。
在基于模型的强化学习中,动力学模型用于进行预测,即动作选择。设 f ^ θ ( s t , a t ) \hat f_{\theta}(s_t,a_t) f^θ(st,at)表示习得的离散时间动力学函数,其参数为 θ \theta θ,取当前状态 s t s_t st和动作 a t a_t at为输入,并在时间 t + △ t t+\bigtriangleup t t+△t输出下一状态的估计。 然后我们可以通过解决以下优化问题来选择操作:

实际上,通常希望在每个时间步求解上述优化问题,仅从输出的行为序列中执行第一个动作,然后在下一个时间步重新规划更新的状态信息。 这种控制方案通常被称为模型预测控制(MPC),并且已知可以很好地补偿模型中的错误。
3. MODEL-BASED DEEP REINFORCEMENT LEARNING
A. 详细描述 f ^ θ ( s t , a t ) \hat f_{\theta}(s_t,a_t) f^θ(st,at)的细节;
B. 如何训练动力学函数;
C. 如何用习得的动力学函数提取策略;
D. 如何利用强化学习进一步提高我们学习的动力学函数。
A. Neural Network Dynamics Function
动力学函数 f ^ θ ( s t , a t ) \hat f_{\theta}(s_t,a_t) f^θ(st,at)被参数化一个权重为 θ \theta θ的深度神经网络。一个简单的参数化是以当前状态 s t s_t st和动作 a t a_t at为输入,输出预测的下一个状态 s ^ t + 1 \hat s_{t+1} s^t+1。然而当 △ t \bigtriangleup t △t很小的时候 s t s_t st和 s t + 1 s_{t+1} st+1区别很小,状态差异并不能很好地说明潜在的动态,进而导致action的选择对输出没有什么影响,模型难以收敛。
为解决这一问题,作者将输出从 s t + 1 s_{t+1} st+1修改为 s t + 1 − s t s_{t+1}-s_t st+1−st。请注意,增加 △ t \bigtriangleup t △t会增加每个数据点的可用信息,并且不仅可以帮助学习动态学习,还可以帮助规划使用习得的动力学模型(第C节)。然而,增加 △ t \bigtriangleup t △t也会增加潜在连续时间动态的离散化和复杂性,这可能使学习过程更加困难。
B. Training the Learned Dynamics Function
-
Collecting training data:
从起始配置中 s 0 ∽ p ( s 0 ) s_0\backsim p(s_0) s0∽p(s0)采样,在每一时间步执行随机策略,记录长度为 T T T的轨迹 τ = ( s o , a 0 , . . . , s T − 2 , a T − 2 , s T − 1 ) \tau=(s_o,a_0,...,s_{T-2},a_{T-2},s_{T-1}) τ=(so,a0,...,sT−2,aT−2,sT−1)。可以看出这些轨迹与训练好的模型最终规划的轨迹区别很大,这显示了基于模型的方法从off-policy数据中学习的能力。 -
Data preprocessing:
将轨迹 { τ } \{ \tau \} {τ}切分为训练数据 ( s t , a t ) (s_t,a_t) (st,at)以及相应的输出标签 s t + 1 − s t s_{t+1}-s_t st+1−st。然后对数据进行标准化,并添加0均值的高斯噪声以增强模型鲁棒性。 -
Training the model:
定义训练集为 D D D,验证集为 D v a l D_{val} Dval。
损失函数定义如下:

虽然这个误差提供了我们所学习的动力学函数在预测下一个状态时的估计能力,但我们实际上想知道我们的模型在预测未来时的能力,因为我们最终将把这个模型用于更长远的控制(参见第C节)。因此,我们通过将学习到的动力学函数向前传播 H H H次来计算 H H H步验证误差,从而进行多步开环预测。对于来自 D v a l D_{val} Dval的每个给定的真实动作序列 ( a t , . . . , a t + H − 1 ) (a_t,...,a_{t+H-1}) (at,...,at+H−1),我们将相应的ground-truth状态 ( s t + 1 , . . . , s t + H ) (s_{t+1},...,s_{t+H}) (st+1,...,st+H)与动力学模型的多步状态进行比较预测 ( s ^ t + 1 , . . . , s ^ t + H ) (\hat s_{t+1},...,\hat s_{t+H}) (s^t+1,...,s^t+H),计算方式为
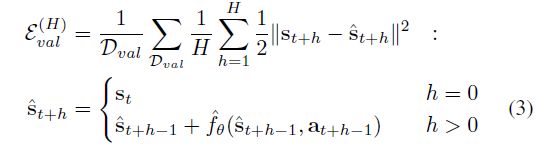
这个 H H H-step验证用于分析我们的实验结果,但在训练中没有使用。
C. Model-Based Control
为了使用习得的模型 f ^ θ ( s t , a t ) \hat f_{\theta}(s_t,a_t) f^θ(st,at),以及对某一任务编码的奖励函数 r ( s t , a t ) r(s_t,a_t) r(st,at),我们设计了一个基于模型的控制器,该控制器在计算上易于处理,并且对学习的动力学模型中的不精确性是鲁棒的。我们首先在有限的长度上优化动作的序列 A t ( H ) = ( a t , . . . , a t + H − 1 ) A_t^{(H)}=(a_t,...,a_{t+H-1}) At(H)=(at,...,at+H−1),用习得的动力学模型来预测未来状态:

由于动力学和奖励函数是非线性的,因此计算上式的精确最优是困难的,但是存在许多技术用于获得足以在期望任务中成功的有限时域控制问题的近似解。在这项工作中,我们使用一种简单的随机抽样shooting method,其中随机生成K个候选动作序列,使用学习的动力学模型预测相应的状态序列,计算所有序列的奖励,并使用选择最高预期累积奖励。与让策略在开环中执行此操作序列不同,我们使用模型预测控制(MPC):策略仅执行第一个操作 a t a_t at,接收更新的状态信息 s t + 1 s_{t+1} st+1,并在下一时间步重新计算最佳操作序列。请注意,对于更高维度的动作空间和更长的视界,使用MPC进行随机抽样可能不够,并且在未来的工作中研究其他方法可以提高性能。
注意,这种结合动力学预测模型和控制器的方法有利于模型只训练一次,但是通过简单地改变奖励函数,我们可以在运行时实现各种目标,而无需执行特定任务的重新训练的情况。
D. Improving Model-Based Control with Reinforcement Learning

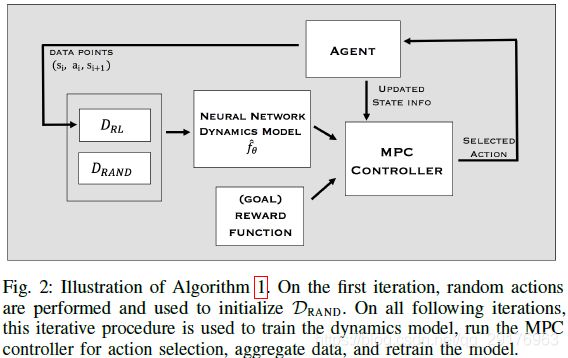
为了提高基于模型的学习算法的性能,我们通过交替使用当前模型收集数据和使用聚合数据重新训练模型来收集附加的on-policy数据。这种on-policy数据聚合(即强化学习)通过减少数据的状态-动作分布和基于模型的控制器分布之间的不匹配来提高性能。算法1和图2概述了我们基于模型的强化学习算法。我们在实验中评估了与数据聚合相关的设计决策(第5-A节)。
4. MB-MF: MODEL-BASED INITIALIZATION OF MODEL-FREE REINFORCEMENT LEARNING ALGORITHM
与无模型算法相比,上述基于模型的强化学习算法可以使用非常少的样本来学习复杂的步态。但是,在基准测试任务中,其最终性能仍然落后于无模型算法。很自然的,我们可以通过使用基于模型的学习器来初始化无模型学习者,将基于模型和无模型学习的优势结合起来。我们提出了一种简单但高效的方法,通过训练模拟我们已学习的基于模型的控制器,然后使用生成的模仿策略作为初始化,将基于模型的方法与现成的无模型方法相结合。
A. Initializing the Model-Free Learner
我们首先根据3-C中所述方法收集MPC控制器生成的示例轨迹,该控制器使用学习到的动力学函数 f ^ θ \hat f_{\theta} f^θ,该函数使用我们基于模型的强化学习算法(算法1)进行训练。我们将轨迹收集到数据集 D ∗ D^* D∗中,然后我们训练神经网络策略 π ϕ ( a ∣ s ) \pi_{\phi}(a|s) πϕ(a∣s)以匹配 D ∗ D^* D∗中的这些“专家”轨迹。我们将 π ϕ \pi_{\phi} πϕ参数化为条件高斯策略 π ϕ ( a ∣ s ) ∼ N ( μ ϕ ( s ) , ∑ π ϕ ) \pi_{\phi}(a|s)\thicksim N(\mu_{\phi}(s),\sum_{\pi_{\phi}}) πϕ(a∣s)∼N(μϕ(s),∑πϕ),其中均值由神经网络 μ ϕ ( s ) \mu_{\phi}(s) μϕ(s)参数化, 并且协方差 ∑ π ϕ \sum_{\pi_{\phi}} ∑πϕ是固定矩阵。 使用行为克隆目标训练此策略的参数
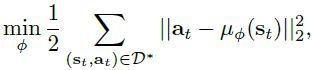
我们使用随机梯度下降进行优化。 为了实现所需的性能并解决数据分布问题,我们应用了DAGGER算法。
B. Model-Free Reinforcement Learning
在初始化之后,我们可以使用策略 π ϕ \pi_{\phi} πϕ作为无模型强化学习算法的初始策略,该策略是由我们基于模型的控制器生成的数据训练的。具体来说,我们使用信任区域策略优化(TRPO);这种策略梯度算法是无模型微调的一个很好的选择,因为它们不需要任何评论家或值函数进行初始化,当然我们的方法也可以与其他model-free RL算法结合使用。
TRPO也是我们考虑的基准任务的常见选择,它为我们提供了一种自然的方式来将纯无模型学习与基于模型的预初始化方法进行比较。使用我们学习的专家策略 π ϕ \pi_{\phi} πϕ初始化TRPO就像使用 π ϕ \pi_{\phi} πϕ作为TRPO的初始策略一样简单,而不是标准的随机初始化策略。虽然这种结合基于模型和无模型的方法非常简单,但我们在实验中证明了这种方法的有效性。
5. EXPERIMENTAL RESULTS
6. DISCUSSION
- 提出了一种基于模型的强化学习算法,该算法能够使用少量样本学习复杂模拟运动任务的神经网络动力学函数(能够解决现有model-based算法难以解决的复杂问题);
- 我们描述了许多有效且高效地训练神经网络动力学模型的重要设计决策,并且我们提出了评估这些设计参数的详细实验。并且该模型可以应用于运行时跟随任务的不同轨迹;
- 基于模型的算法本身并不总能达到极高的奖励,但它通过允许成功提取复杂和逼真的步态提供实际用途。一般而言,我们基于模型的方法可以很快胜任任务,而无模型方法需要大量数据,但可以成为专家;