强化学习知识总结

概览

之前学习了李宏毅老师深度学习中，关于深度强化学习的相关知识，感觉虽然推导公式基本都已经了解了，但是印象却不是十分深刻，因此，在这里写下来用作复习。
本次内容主要关注的是model-free的部分，对于model-base的内容，在这次就不进行深入的探讨了。这个博客会首先从policy-base的方法开始讲起，然后过渡到value-base的方法。最后再讲讲比较著名的A3C是如何将两者结合起来进行使用的。值得注意的是老师在课程的最后向同学们介绍了模仿学习(imitation learning)，但是在这篇文章中我们不会探讨这个问题，我之后会专门开一个新的系列来讲一讲我认识中的模仿学习以及其中的反向强化学习（inverse reinforcement learning）
补充：在全部写完之后，补充一下on-policy 和 off-policy 两种不同的训练方法（参数更新）

强化学习的基本分类

model-based approach

在这个方法下面，机器会对环境有一个详细的认知，也就是可以在不打开游戏的环境下进行模拟，我们称之为simulator

model-free approach

policy-base 用奖励梯度来表示策略梯度，直接更新策略 $\pi$

value-base 不直接更新策略 $\pi$，而是更新未来预期函数Q来间接影响策略 $\pi$

Policy based approach

1.基本定义

1. $a=\pi (s)$
   $\pi$表示策略，$\theta$是这个策略的参数（如果线形表示的话，那么实际上$a=\theta s$），它的输入是状态s，输出是动作a

2. $\pi (s,a)=\pi (a|s)=P(a|s)$
   在状态s下进行动作a的概率也可以表示称这种形式

3. $R_{\theta }={\sum }_{t=1}^T{r}_t$
   我们将从游戏从开始到结束，agent得到的奖励成为total reward

4. $\tau =\{s_1,a_1,r_1.......,s_T,a_T,r_T\}$
   我们将这个有序列表称为trajectory

5. $P(\tau |\theta )=P(s_1){\prod }_{t=1}^{T}p(a_t|s_t,\theta )p(r_t,s_{t+1}|s_t,a_t)$
   在策略$\theta$下选择路径$\tau$的概率不难理解可以表示为左边的等式，但是值得注意的是，这个公式的第一项和第三项都和你的actor无关，都是只取决于environment的。

6. $\overline{R_{\theta }}={\sum }_{\tau }R(\tau )P(\tau |\theta )\approx \frac{1}{N}{\sum }_{n=1}^{N}R(\tau )$
   我们将这个称为策略$\theta$的奖励期望，也是我们在求奖励梯度时会着重使用的公式

7. on-policy:真正进行学习的agent和与环境互动的agent是同一个agent
   off-policy:真正进行学习的agent和与环境互动的agent不是同一个agent

   我们现在来深入思考一下为什么会有off-policy的存在。on-policy需要我们在每一次$\theta$更新之后，重新进行采样，这样的话算法效率过低，因此我们引入off-policy来解决这个问题。

2.主要方法

我们主要通过求上面奖励期望对$\theta$微分来表示我们的策略梯度，然后我们对这个进行梯度上升（gradient ascent），用这个方法不断逼近理想中的最佳策略$\theta$，而在深度学习当中，我们会把这个$\theta$写成一个神经网络的形式。

2.1公式推导

1. problem statement: ${\theta }^{\ast }=argmax\overline{R_{\theta }}$

2. gradient ascent: ${\theta }_{new}={\theta }_{old}+\eta \nabla \overline{R_{{\theta }_{old}}}$

3. calculate about the gradient$\nabla \overline{R_{\theta }}$:
   $\nabla \overline{R_{\theta }}={\sum }_{\tau }R(\tau )\nabla P(\tau |\theta )$
   $={\sum }_{\tau }R(\tau )P(\tau |\theta )\frac{\nabla P(\tau |\theta )}{P(\tau |\theta )}$
   $={\sum }_{\tau }R(\tau )\nabla log(P(\tau |\theta ))$
   $\approx \frac{1}{N}{\sum }_{n=1}^{N}R({\tau }^n)\nabla log(P(\tau |\theta ))$
   然后在这里我们将微分算符后面的内容展开，表示形式如下：
   $log(P(\tau |\theta ))=log(p(s_1))+{\sum }_{t=1}^T(log(p(a_t|s_t,\theta ))+p(r_t,s_{t+1}|s_t,a_t))$

   观察这个式子我们不难发现，第一项和第三项军事由environment决定的，也就是说不包含我们的微分对象$\theta$，所以在微分后就会消失，由此我们可以将策略梯度表示成如下的形式：
   $\nabla \overline{R_{\theta }}=\frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T^n}R({\tau }^n)\nabla log(P(a_t^n|s_t^n,\theta ))$

   那么我们不妨在这个位置，理解一下策略梯度的具体含义，从这个式子我们不难看出，当我们的一条路径收获正向的奖励的时候，我们进行这个路径中的行为的概率就会被增加，这种增加会表现在参数$\theta$的增加上面。

   甚至，我们可以再进一步的思考一下，深度强化学习种的policy based方法和图像的classfication究竟有什么样的相似之处。通过观察两者的梯度公式，我们不难发现，其实a就是我们的图像分类中的标签，而奖励不过只是一种我们添加上的权重而已。

   但是，这时候我们会发现，这个更新的方法似乎存在一个问题，那就是在一个得到正向奖励的路径当中，所有的行为进行的概率都会增加，但是事实上，正向奖励的路径中并不一定所有的动作都具有正向的奖励。同时，当环境所有的奖励都是正向的时候，而且如果我们在进行更新的时候采样不足的话，那就可能会出现一种情况，我们大量采样了那些不算十分成功的动作，从而导致了更好动作发生的概率相对来说发生了下降。（但是之后我们会介绍一种算法来解决这个问题）

2.2PPO

PPO全称是proximal policy optimization，是目前openAI的baseline的重要算法，其实就是在原先的策略梯度上面加上了KL散度。但是在正式开始之前，我们需要先解决上面公式推导中所提出的问题(两个小tips)，之后在解释我们是如何把KL散度加上去的。

Tip one:add a baseline

$\nabla \overline{R_{\theta }}=\frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T^n}(R({\tau }^n)-b)\nabla log(P(a_t^n|s_t^n,\theta ))$
$b=E(R(\tau ))$

Tip two:assign a suitable credit to replace $R({\tau }^n)$

$\nabla \overline{R_{\theta }}=\frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T^n}({\sum }_{t^{,}=t}^{T^n}{\gamma }^{t^{,}-t}{r}_t^n-b)\nabla log(P(a_t^n|s_t^n,\theta ))$

$A^{\theta }(s_t,a_t)={\sum }_{t^{,}=t}^{T^n}{\gamma }^{t^{,}-t}{r}_t^n-b)$

这时我们将定义一个新的函数$A^{\theta }(s_t,a_t)$。这个函数会告诉我们在$s_t$的情况下，采取行动$a_t$究竟和其他动作相比，是好还是坏,$\gamma$是折扣系数（0<$\gamma$<1）。

2.2.1如何导出PPO

我们想要在策略梯度的原函数上添加KL散度来帮助我们改善原本的性能不足，那么我们首先就需要推导，如何能得出策略梯度的原函数。那么我们这里就不得不介绍一下一个重要的采样方式（importance sampling）,同时由于PPO本身是off-policy的，我们还需推导一下on-policy究竟是如何变成off-policy

importance sampling

假设存在一个问题，要求我们求解函数f(x)在未知分布P上的期望，那么我们就可以引入一个已知的分布Q来“映射到”分布P上来解决这个问题（即x采样自分布q）。
$E_{x\sim p}[f(x)]=\int f(x)p(x)dx=\int f(x)\frac{p(x)}{q(x)}q(x)dx=E_{x\sim p}[f(x)\frac{p(x)}{q(x)}]$
但是我们需要注意的是，虽然这两个分布这样计算的时候，他们的期望是一样的，但是事实上，他们两者的方差只有在sample的数量足够多的情况下才相等，感兴趣的话可以用方差的定义自行推导一下，这里就不赘述了

From gradient to Primitive

$gradient=E_{(st,at)\sim {\pi }_{{\theta }^{,}}[A^{\theta }(s_t,a_t)\nabla log(P_{\theta }(a_t^n|s_t^n))]}$
$=E_{(st,at)\sim {\pi }_{{\theta }^{,}}[A^{{\theta }^{,}}(s_t,a_t)\frac{p_{\theta }(s_t^n,a_t^n)}{p_{{\theta }^{,}}(s_t^n,a_t^n)}\nabla log(P_{\theta }(a_t^n|s_t^n))]}$
$=E_{(st,at)\sim {\pi }_{{\theta }^{,}}[A^{{\theta }^{,}}(s_t,a_t)\frac{p_{\theta }(a_t^n|s_t^n)p_{\theta }(s_t^n)}{p_{{\theta }^{,}}(a_t^n|s_t^n)p_{{\theta }^{,}}(s_t^n)}\nabla log(P_{\theta }(a_t^n|s_t^n))]}$
$=E_{(st,at)\sim {\pi }_{{\theta }^{,}}[A^{{\theta }^{,}}(s_t,a_t)\frac{p_{\theta }(a_t^n|s_t^n)}{p_{{\theta }^{,}}(a_t^n|s_t^n)}\nabla log(P_{\theta }(a_t^n|s_t^n))]}$

这里我们将$p_{\theta }(s_t^n)$和$p_{{\theta }^{,}}(s_t^n)$同时去掉的原因，老师只从很直观的角度进行了解释，具体的解释应该恨数学，我们这里就不谈了。从直观的角度来看，因为从MP过程的角度来看，你进入这个状态的概率和你采取什么样的策略无关，因此两者在这个地方其实是相同的，因此可以同时消去。

根据$\nabla f(x)=f(x)\nabla logf(x)$,我们可以得到原函数(object function)：

$J^{{\theta }^{,}}(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }^{,}}}[A^{{\theta }^{,}}(s_t,a_t)\frac{p_{\theta }(a_t^n|s_t^n)}{p_{{\theta }^{,}}(a_t^n|s_t^n)}]$

而对于PPO而言，这里用一个折扣系数乘上KL散度，来作为全新的原函数（object function）：

$J_{ppo}^{{\theta }^{,}}(\theta )=J^{{\theta }^{,}}(\theta )-\beta KL(\theta ,{\theta }^{,})$

$\{\begin{array}{r}ifKL(\theta ,{\theta }^{,})>K{L}_{max}\upharpoonleft \beta \\ ifKL(\theta ,{\theta }^{,})>K{L}_{max}\downharpoonleft \beta \end{array}$

值得注意的是，这里面$\theta$和${\theta }^{,}$的KL散度不是两个参数分布上的差异，而指的是以state为横轴，action为纵轴的分布之间的距离。而当KL散度过大时，说明目标分布和我们已知道预设分布差异较大，说明这个惩罚项效果不明显，因此应该加大$\beta$，但是当KL散度较小的时候，说明目标分布和和我们已知道的预设分布差异较小，说明效果过强，因此需要减少$\beta$。

补充：PPO2

老师在最后，介绍了PPO的简化实现版本，效果不错，也比较好理解，这里就不详细来写了，感兴趣的话可以点这个链接进去了解（原文地址）

value based approach

1.基本定义

1. Critic:评价者并不会真的决定采取什么样的action，我们会在一个给定的actor（换言之，一个给定的策略）下面来评估这个actor的好坏程度。
2. state-value function($V^{\pi }(s)$):在一个给定的actor $\pi$ 的情况下，我们在观察到状态s之后，累积的期望奖励就是我们的$V^{\pi }(s)$。
3. state-action value function($Q^{\pi }(s,a)$):当我们使用actor $\pi$ 的时候,在观察到s，并给定动作a的情况下累积预期奖励的值（scalar）就是$Q^{\pi }(s,a)$。

2.如何估计$V^{\pi }(s)$：

1）monte-carlo based approach:
critic观察actor游玩这个游戏的全过程，在输入一个一个状态s之后，输出的是预计的累积奖励($V^{\pi }(s)\leftrightarrow G_a$)。

S

值函数的神经网络

Ga

2)Temporal difference(TD) approach:
这个方法主要用在一个难以结束的游戏上面，比如模拟人类的行走等任务。我们在这种情况下，智能获得一部分的互动过程,表示如下：
$V^{\pi }(s_t)=r_t+V^{\pi }(s_{t+1})$

St

值函数的神经网络

V_t-V_t+1

St+1

值函数的神经网络

DQN

1.基本的Q学习流程

${\pi }^{,}(s)=argma{x}_a{Q}^{\pi }(s,a)$

我们可以这样理解这个式子，Q会对所有当前的（s,a）给出一个Q值，选择可以使得这个Q值最大的动作，而这个动作也就是我们的策略所会在这个state下选择的action。

并且${\pi }^{,}$不会含有额外的参数，它完全依赖于Q。且不适用于连续情况，因为Q矩阵的大小是有限的。

2.Target network

我们现在知道了要求解Q(s,a)的最大值，但是具体求解流程还不是十分明晰，这里以一张图片的形式来介绍我们具体训练的方法。

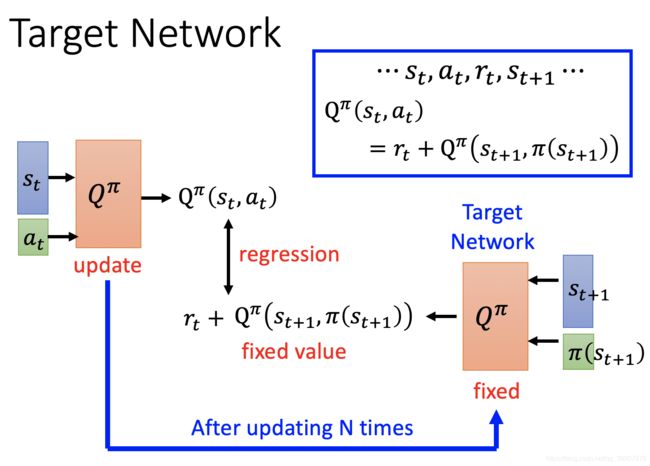
目标网络和训练网络是不同的Q网络，这个网络的参数是固定的，因此给出的target的也是固定的，可以让regression的时候label固定，更加稳定。因此在实际训练的过程当中，（最开始的时候是一样的两个网络）我们一般都是训练几次之后更新一次目标网络，之后继续训练，在一段时间之后再更新目标网络。

3.Exploration

我们都知道Q学习的基本操作方法是${\pi }^{,}(s)=argma{x}_a{Q}^{\pi }(s,a)$，但是事实上这并不是一个对数据很好的方法，因为我们得到的情况动作组合会十分有限，无法遇到足够多的特殊情况，从而导致agent的性能并不是十分很好，因此我们需要有一种方法可以让我们的agent进行一些对环境空间的探索。

$a\{\begin{array}{r}argmaxQ(s,a)withprobability1-ϵ\\ randomwithprobabilityϵ\end{array}$

但是上面的这种基本的探索方法存在一个问题，就是探索并不会基于当前的state和action给出，是完全随机的，从一般思维的角度来看，其实还是用类似于GA那种轮盘赌方法来选择探索会效果更佳，我们在这里称之为Boltzmann Exploration:

$p(a|s)=\frac{exp(Q(s,a)}{{\sum }_a(Q(s,a))}$

4.Reply Buffer

我们会把每次和环境互动的记录存放在一个经验回放的buffer里面，每次我们都会从中随机选出一部分数据，用来进行训练，更新我们的Q网络。经验回放会存放不同policy留下的经验，但是当buffer充满的时候，我们会丢弃最老的经验。

5.Typical DQN

注：因为这个算法中的Q是一个神经网络，因此这其实是一个DQN的算法

6.DQN存在的问题

我们观察目标网络会发现，每一次我们的目标值实际上都是我们猜测出来的，并且因为TD的关系，我们每次都会取最大值，这就会导致实际上我们的估测目标值永远偏大，导致结果不好，因此我们会有很多方法解决这个问题（double-DQN,duel-DQN等等，这里感兴趣的话可以自行查询）
同时我们应该注意到我们目前的DQN无法应对动作连续的情况，因此我们在这里特别给出解决连续动作问题的DQN。

DQN for continuous action

这里面除了$\sum (s)$都十分好理解其含义，且教授并没有解释$\sum (s)$，因此这里就当它是一个matrix，不管含义的直接用好了。

Actor-Critic

当我们将policy based和 value based结合起来之后，就是最近几年比较流行的算法A3C(Asynchronous advantage actor critic)了。

Advantage actor critic

上面这个是A2C，比较好理解的是，原本的策略梯度下降当中的baseline和累积奖励，变成了V的形式。但对于A3C来说，会像鸣人影分身修行一样，不同的子网络各自训练，但是都会更新在一个全局网络上（gobal network）

注：微分算符写错了

Pathwise Deviate Policy Gradient

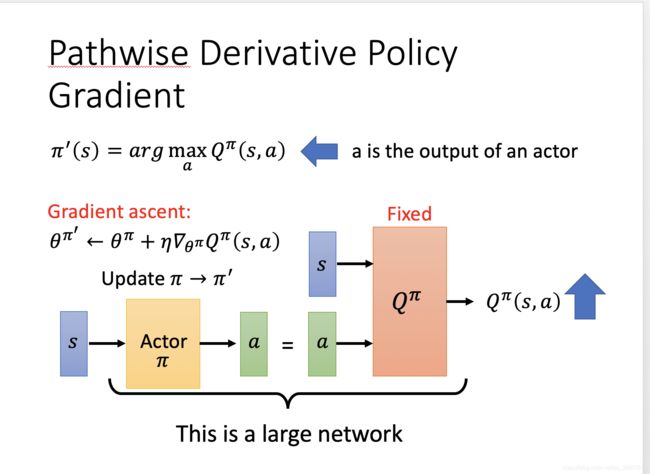
网络结构如图所示，我们在训练的时候，先训练后半部分的Q网络，之后固定住这个网络，再训练我们的actor。在某种程度上，这个和GAN有些类似，但是GAN在训练的时候是同时的，而这个网络的训练是异步的。

Sparse reward and imitation learning

老师在这里简单介绍了四个小tips来解决稀疏奖励的问题，imitation learning可以用来解决甚至是完全无法获得奖励的任务。由于我的目前的研究防线是模仿学习下的反向强化学习，因此在未来我还会结合代码来认真分析一下反向强化学习的结构和原理。

1. reward shaping
2. curiosity(intrinsic curiosity module)
3. curriculum learning and reverse curriculum generation.
4. Hierarchical reinforcement learning

future work

接下来，我会试着结合代码谈一谈反向强化学习，以及GAIL等比较新的模仿学习的模仿学习领域的算法以督促自己好好读论文写代码。