【深度】Dual Representation | 强化学习前沿

今天，你AI了没？

关注：决策智能与机器学习，学点AI干货

对偶理论是研究线性规划中原始问题与对偶问题之间关系的理论。 对偶形式是解决优化问题的一种有效办法，即每一个线性规划问题（称为原始问题）有一个与它对应的对偶线性规划问题（称为对偶问题），在求出一个问题解的同时，也给出了另一个问题的解。可以说是优化求解中四两拨千斤的方法。

本文讨论的就是强化学习问题的对偶形式求解问题。

友情提示：技术深度解读，文中大量公式，公式恐惧症的同学慎入。

原文下载，请在公众号回复：20190620

特色

考虑找到MDP上的最优策略使得累积奖励最大，如果已知 dynamics（P）和 reward（R）那么该问题是一个动态规划问题（DP），又称作规划问题（planning problem）；如果这两者未知只能通过和环境交互得到，那么该问题是一个强化学习问题（RL），又称作学习问题（learning problem）。相应的动态规划问题可以表示为一个线性规划问题（LP，可以参见我导师的讲义），相应地，该问题就其对偶形式。前面讲到的 successor representation （SR）就实际上是在解相应的对偶问题。本文给出了 DP 和 RL 问题的相应对偶形式，具体地，给出了对偶形式的 policy evaluation、policy iteration、TD evaluation、SARSA、Q-learning。

过程

这篇文章都是矩阵-向量表示形式，需要注意符号定义，特别是维度。

1. 线性规划及其对偶问题

考虑一个规划问题，它可以写为 LP 的形式

其中  是初始状态分布，  ，  ，  。要证明它的解是规划问题的解，只需要证明相应的  满足 Bellman equation  。对于任意一个状态  ，只要  ，我们都可以只减小  的值并且不与其他的约束条件冲突，考虑到  ，这样的操作一定使得目标函数更优。反复这样操作可以得到 。

相应的最优策略可以写为

简要地来说，转化为对偶问题的步骤是，先写出 LP 的拉格朗日函数  ，然后令  对原变量求导为零，把拉格朗日乘子作为新的变量。相应的对偶关系可以说明对偶问题的最优解和原问题最优解之间的关系。下面就按照这些步骤来做。

其拉格朗日函数可以写为

其中  为拉格朗日乘子，  只含有0和1，只是把原问题里面的约束条件表示为矩阵形式。

拉格朗日函数对  求导并且令其为零，可以得到

将其代回拉格朗日函数，可以得到相应的对偶问题

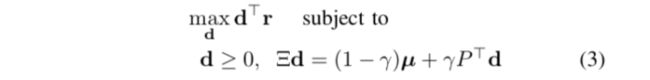
对偶问题里面的约束条件要求  是一个在 state action 上的概率分布，即

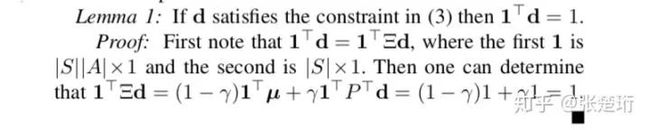
根据对偶关系，最优策略和对偶问题的最优解有如下关系

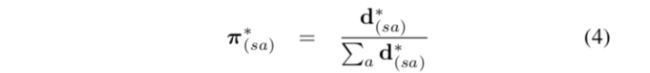
对偶问题的最优解其实就是从规定初始状态开始、遵循最优策略，相应得到的 discounted state-action visits。

2. Policy evaluation （state value function / V function）

给定一个策略，把它表示为一个  的矩阵

考虑到  是一个  的矩阵，由此  表示在相应策略下的一步状态转移矩阵，  表示在相应策略下的一步 state-action 转移矩阵。

V函数可以表示为

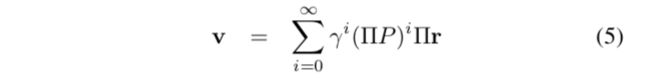
也可以表示为  。

如果令（即前面所说的 successor representation，不过相差了一个常系数  ）

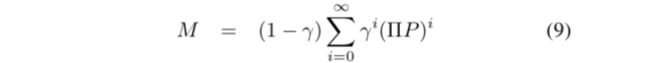
那么V函数就可以由它表示出来：  。

3. Policy evaluation （state action value function / Q function）

Q函数可以表示为

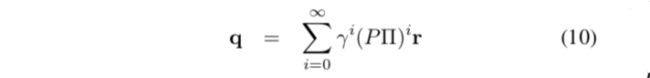
它满足如下递归关系  ，和相应V函数之间满足关系  。

令（state-action形式下的 successor representation）

那么Q函数就可以由它表示出来：  。同时，它和SR有如下关系  。

4. Policy iteration

Policy iteration 包含 policy evaluation 和 policy improvement，前者在前面两个部分已经说明了，policy improvement 需要每次采取使当前状态下Q函数最大的行动，或者采取一个行动使得其到达的下一个状态有更大的V函数值。即

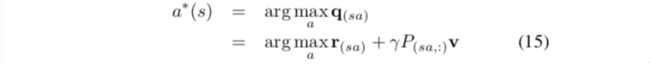
写成对偶形式有

最后可以得到对偶形式下的policy iteration。

5. TD evaluation / SARSA / Q-learning

前面都是考虑 planning 的情形，现在考虑 learning 的情形。不难得到，SR 可以通过 TD-learning 的方式来学习。

SARSA 分为 policy evaluation 和 policy improvement，其中 policy evaluation 步骤更新估计 on-policy 的 SR，可以写为如下形式

Q-learning 在更新的过程中隐含了 policy improvement 步骤，可以写为

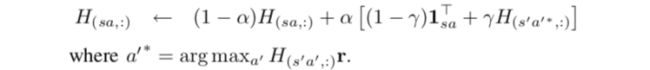
作者 | 张楚珩（清华大学 交叉信息院博士在读）

来源 | 知乎专栏：强化学习前沿

原文地址 | https://zhuanlan.zhihu.com/p/69697253

经作者授权转载

相关推荐

• 【重磅】《演化学习：理论与算法进展》| 南大周志华、俞扬、钱超重要成果
  

• 强化学习 | 基于强化学习的机器人自动导航技术

• 深度强化学习的经典入门课程（附链接） | 课程地图

• 干货 | 深度强化学习国际顶会ICML-2019最新进展速览—论文PDF打包下载

• 最新 | 用深度强化学习打造不亏钱的交易机器人（附代码）

   交流合作

商务合作以及加入微信群，请添加微信号：yan_kylin_phenix

注意：请务必说明您的意向，注明姓名+单位+从业方向+地点，否则不予通过，请多谅解。