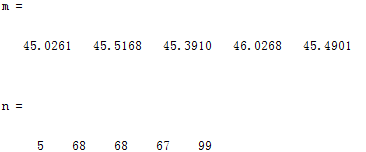matlab多项式计算与数据处理

1．掌握数据统计和分析的方法
2．掌握数值插值与曲线拟合的方法及其应用
3．掌握多项式的常用运算

（多项式必须保证对应长度相等才能相加减）
有3个多项式试进行下列操作：
（1）求P(x)=p1(x)+p2(x)p3(x)。
（2）求P(x)的根。
（3）当x取矩阵A的每一元素时，求P(x)的值。其中：

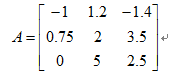
（4）当以矩阵A为自变量时，求P(x)的值。其中A的值与第（3）题相同。*

n次多项式中将其系数从最高阶到0阶依次组合，写成向量形式，即P0=[…… a3 a2 a2 a0]。

p0=[1 2 4 0 5];
pq=[1 2];
pw=[1 2 3];
syms x;
p1=poly2sym(p0)
p2=poly2sym(pq)
p3=poly2sym(pw)

后面的按着写就行，这种类型的题注意点就是维度必须要保持一样

已知lgx在[1，101]区间10个整数采样点的函数值如实验1所示

试求lgx的5次拟合多项式p(x)。其中lgx所用到的函数为log10(x)。

x=1:10:101;
y=log10(x);
polyfit(x,y,5);

3、 利用MATLAB提供的randn函数生成符合正态分布的10*5随机矩阵A，进
行如下操作：
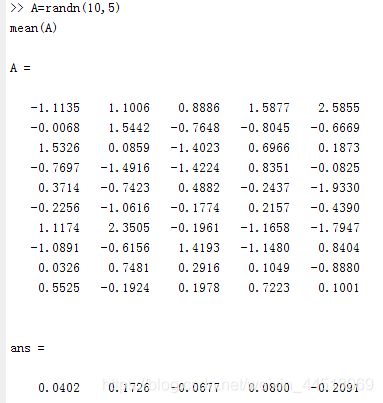
（1）A各列元素的平均值

A=randn(10,5)
mean(A)

（2）A的最大元素和最小元素。

max(max(A))
min(min(A))

（3）求A每行元素的和以及全部元素之和。用sum()函数

sum(A,2) 或sum(A’)
sum(sum(A))

（4）分别对A的每列元素按升序、每行元素按降序排序。

sort(A)
-sort(-A,2)

4、 将100个学生5门功课的成绩存入矩阵P中，进行如下处理：
（1） 分别求每门课的最高分，最低分及相应学生序号。
（2） 分别求每门课的平均分。教材P58中表3-2。
（3） 5门课总分的最高分、最低分及相应学生序号。
（4） 将5门课总分按降序存入zcj中，相应学生序号存入xsxh。
提示：上机调试时，为避免输入学生成绩的麻烦，可用取值范围在[45，95]之间的随机矩阵来表示学生成绩。

P=45+(95-45)*rand(100,5);
(1)[x,y]=max(P);[m,n]=min(P)

(2)mean(P)

(3)[x,y]=max(sum(P,2)); [x1,y1]=min(sum(P,2))

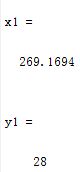
(4)[zcj,xsxh]=sort(-sum(P,2));zcj=-zcj

5、 某气象观测站测得某日6:00~18:00之间每隔2h的室内外温度（℃）如实验表2所示

试用三次样条插值分别求出该日室内外6:30~17:30之间每隔2h各点的近似温度

 h=6:2:18;
t1=[18 20 22 25 30 28 24];
t2=[15 19 24 28 34 32 30];
h1=6.5:2:17.5
z1=interp1(h,t1,h1,'nearest')
z2=interp1(h,t2,h1,'spline')
subplot(1,2,1)
plot(h,t1,'o',h1,z1,'-')