Codeforces Round #665 (Div. 2)A-D题解

** Codeforces Round #665 (Div. 2)A-D题解**
//写于rating值2075/2184
//下午刚补的题，28号之前都要练科三，这段时间的比赛应该都要鸽了

比赛链接:https://codeforces.com/contest/1401
A题
简单思维

题意为在x轴上有一个点A位于（n,0），现在给定一个值k，你需要找到一个点B位于（m,0）满足m<=n，使得原点（0，0）到B的距离与A到B的距离的差的绝对值等于k。（n,m,k均为整数）
如果无法找到这样的点，我们可以对点A进行任意次操作，每次操作我们可以使n的值增大或减小1。
现在需要你输出最小的操作次数，使得我们可以找到满足要求的点B。

首先当n=k的情况下，我们可以选择B点为（0，0），这样的情况下OB长度为0，AB长度为n=k，两段距离差值为k满足要求，需要操作次数为0。

如果n

如果n>k的话，此时并不是说必定不需要操作的。还需考虑n和k的奇偶性。假设OB长度为L1,AB长度为L2，且L1>L2，由于n,m,k都必须是整数，因此L1和L2的长度也为整数。
已知L1+L2=n，L1-L2=k，得L1=L2+k
得2$\times$ L2=n-k，也就是说n-k必须是偶数。
因此当n-k不为整数时，我们还需要对n进行一次+1的操作。

#include
#define ll long long
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
int32_t main()
{
    IOS;
    int t;
    cin>>t;
    while(t--)
    {
        ll n,k;
        cin>>n>>k;
        if(k<n) cout<<(n-k)%2<<endl;
        else cout<<k-n<<endl;
    }
}

B题
分类，贪心，简单思维

现在有两个数列只包含0，1，2，两个数列长度相等。
第一个数列有a1个0，b1个1，c1个2。
第二个数列有a2个0，b2个1，c2个2。

现在你需要对这两个数列的数字两两配对，
设第一个数列中选出的数字为x，第二个数列中选出的数字为y
当x=y时，累加0到答案上
当x>y时，累加x$\times$ y到答案上
当x$\times$ y到答案上

现在需要你输出最终答案可能的最大值。

这道题每个数列中只有0,1,2三种数字，且存在0，最后的计算又是乘法。我们直接讨论下9种情况很容易发现，
只有当x=2,y=1的时候，会对最终答案有正增加，
只有当x=1,y=2的时候，会对最终答案有负增加，
其他情况对答案的增加都是0。

而正增加和负增加的两种选择是不冲突的，我们直接贪心选取最多对数的正增加和最少对数的负增加即可。

我们能增加的最多对数的x=2,y=1，为第一个数列中2的个数和第二个数列中1的个数的最小值。
在这之后我们希望x=1,y=2的对数尽可能少，那么我们让第二个数列中的2尽可能先与第二个数列中的0和2配对，剩下的只能与1配对，这种情况下即为最少配对数。

#include
#define ll long long
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
int32_t main()
{
    IOS;
    int t;
    cin>>t;
    while(t--)
    {
        ll a1,b1,c1,a2,b2,c2;
        cin>>a1>>b1>>c1>>a2>>b2>>c2;
        ll ans=0;
        ll temp=min(c1,b2);//考虑我们增加的2*1的对数最多有多少
        ans+=temp*2;c1-=temp;//累加到答案上，并且减去使用掉的第一个数列中的2的个数
        temp=max(0ll,c2-c1-a1);//考虑减少的1*2的对数最少有多少
        //我们尽可能让第二个数列的2与第一个数列的2或者0配对，剩下的无可奈何只能与1配对
        //这里要和0取个max，因为c2-c1-a1可能为负数。
        ans-=2*temp;
        cout<<ans<<endl;
    }
}

C题
排序，整体思维

给定一个长度为n的数列，其中最小的数字为Min，你每次可以选择这个数列中两个下标不同的数字x和y满足gcd（x,y）=Min，交换这两个数字的位置。
现在询问你是否可以通过任意次上述操作后，使得数列变为从小到大排序的数列。

首先要认识到一点，原数列中，数值无法整除Min的，代表其因子中根本不含有Min，那么它与其他数字的gcd必定不为Min，因此它的位置是不可改变的。

那么原数列中 ，排除掉无法整数Min的数，剩下的那些可以整除Min的数字，我们又可以通过题意给定的操作把它们排序到什么程度呢?
数列中必然有一个数字是等于Min的，Min与任何一个可以整除它的数字的gcd必然等于Min，也就是说Min这个数字是可以与任意其他剩下的数字交换位置的。
一旦有一个数字满足了上述的可以与任意其他位置的数字交换位置，我们就可以通过这个数字进行类似插入排序的过程，把整个数列都排序完毕。

也就是说，数值无法整除Min的数字们，我们是无法改变它们的位置的，而可以整除Min的数字们，我们是可以将他们按照从小到大排序好的。

由此我们直接对原数列排序，注意数值相等的时候要按照下标从小到大排序，因为无法整除Min的数字可能数值相等，而他们的位置是不可改变的，也就是原数列中的先后顺序应当被保留。因此我们不可以直接使用不稳定的快速排序。检测一下无法整除Min的数字，它们排序后所在的位置下标是否都与原位置下标相同，如果不同则代表无法构造。

#include
#define ll long long
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
#define llINF 9223372036854775807
const ll maxn=1e5+7;

struct Node
{
    ll data,tar;
};

ll n,Min;//Min为数列中的最小值
vector<Node>node;

bool cmp(Node a,Node b)//数值为第一排序关键字，数值相等时按照原下标从小到大排序
//即一个稳定的快速排序
{
    if(a.data!=b.data) return a.data<b.data;
    else return a.tar<b.tar;
}

int32_t main()
{
    IOS;
    int t;
    cin>>t;
    while(t--)
    {
        cin>>n;
        node.resize(n);
        Min=llINF;
        for(ll i=0;i<n;i++)
        {
            cin>>node[i].data;
            node[i].tar=i;
            Min=min(node[i].data,Min);
        }
        sort(node.begin(),node.end(),cmp);
        bool flag=1;
        for(ll i=0;i<n;i++)
        {
            if(node[i].data%Min&&i!=node[i].tar) flag=0;
            //如果当前的数值无法整除Min那代表它是无法被交换位置的
            //如果在稳定排序后的位置与其原位置不同，那么代表我们是无法得到稳定排序后的数列的
        }
        if(flag) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
        node.clear();
    }
}

D题
贪心，简单图结论

给定一棵树有n个结点，n-1条边。现在需要你对每条边给定一个数值，这n-1条边对应的数值相乘需要等于给定的数字k。由于k可能会非常庞大，题目输入数据为k分解质因子后的结果。

现在需要使得累加所有任意两点间的简单路径的边的数值和，这个最后的结果要尽可能大，且对每条边构造数值的时候，1的数量要尽可能的少。

我们首先需要想到的，对于这棵树上的每条边，他在最后的结果中被累加了多少次呢。
以题目的第一个样例的图为例:

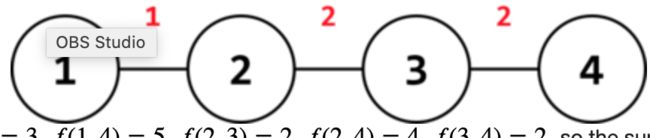
在上图中，中间的这条边，左侧有两个点1和2，右侧有两个点3和4。这条边总共被计算了2 $\times$ 2=4次。也就是左侧的节点个数乘以右侧的节点个数，因为左侧的点到右侧的点的简单路径必然要经过当前这条边。而左侧的点走到左侧点或是右侧的点走到右侧的点的简单路径，是不需要经过当前边的。

我们可以通过一遍从根节点出发的dfs计算出每个节点的子节点数，并由此计算出每条边在最后的结果中被计算了多少次。

之后是对这n-1条边如何构造数值的过程了。
题目要求这n-1条边的数值乘积要等于k，那么必然的他们分解质因数的结果要与k相同。
当k分解质因数得到的质因子个数m<=n-1的时候，我们直接采用贪心的过程，按照质因子个数大的与边在最后结果中出现次数的进行两两配对即可。m 当m>n-1的时候。同样采用贪心的策略，我们让最大的m-(n-1)+1个质因子累乘起来，放在出现次数最大的边上。（这个贪心的正确性可以用反证法来证明）。之后采取与上种情况同样的贪心配对过程即可。

#include
#define ll long long
#define IOS ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
using namespace std;
const ll mod=1e9+7;

ll n,m,start;
vector<vector<ll>>to(1e5+7);//存边
vector<ll>sun;//sun[i]记录结点i包括自己有几个子节点，用于计算边被计算几次
deque<ll>k;//k分解质因子后得到的数列
deque<ll>edgenum;//存储每条边各自会被计算多少次累加到结果上，排序后用于贪心过程

void dfs(ll now,ll pre)//now为当前所在节点,pre为上一个节点
{
    for(ll i=0;i<to[now].size();i++)
    {
        if(to[now][i]!=pre)//不往回走
        {
            dfs(to[now][i],now);
            sun[now]+=sun[to[now][i]];//累加子树的子节点数当前节点上
        }
    }
    sun[now]++;//自身也算做一个子节点
    if(now!=start) edgenum.push_back((n-sun[now])*sun[now]);
    //对于now到pre的这条边来说，sun[now]为这条边“下面”的子节点数，那么n-sun[now]即为这条边"上面"的子节点数
}

int32_t main()
{
    IOS;
    int t;
    cin>>t;
    while(t--)
    {
        cin>>n;
        for(ll i=1;i<=n;i++)
            to[i].clear();
        for(ll i=1;i<n;i++)
        {
            ll u,v;
            cin>>u>>v;
            to[u].push_back(v);
            to[v].push_back(u);
        }
        cin>>m;
        k.resize(m);
        for(ll i=0;i<m;i++) cin>>k[i];
        sort(k.begin(),k.end());//排序用于贪心
        for(ll i=1;i<=n;i++)//找一个出度为0的点，作为树的根进行dfs
            if(to[i].size()==1) start=i;
        sun.clear();sun.resize(n+1,0);
        edgenum.clear();
        dfs(start,-1);//dfs计算每条边会被计算几次到答案上，也就是每条边的权值
        sort(edgenum.begin(),edgenum.end());//排序用于贪心
        while(m>edgenum.size())//m为k数组的大小，如果m的个数大于边的个数，我们要贪心使得权值最大的边对应最大的乘积
        //不断累乘最大的值给第二大的数，缩小数组大小即可
        {
            k[m-2]=(k[m-2]*k[m-1]%mod);
            k.pop_back();
            m--;
        }
        while(m<edgenum.size())//再考虑m个数小于边的个数时，我们需要在剩下的边补1
        {
            k.push_front(1);
            m++;
        }
        ll ans=0;
        for(ll i=0;i<m;i++)//贪心过程，小的值配权值小的边，不断累加到答案上
        {
            ans=(ans+edgenum[i]%mod*k[i]%mod)%mod;
        }
        cout<<ans<<endl;
    }
}