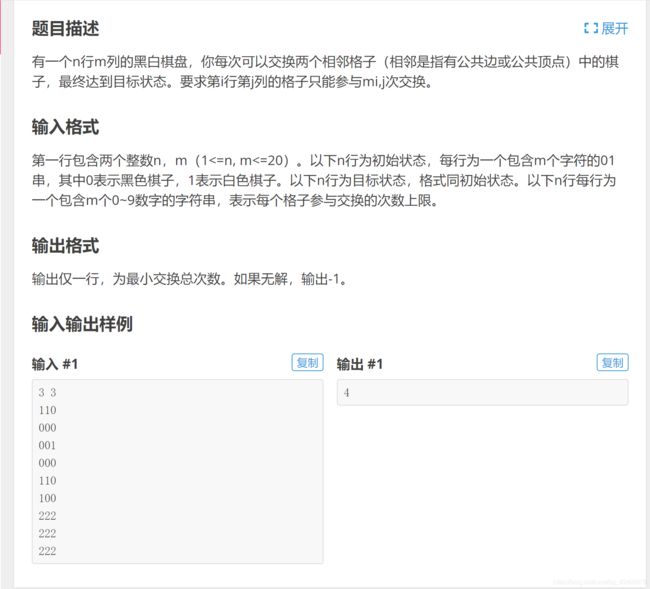
交换棋子题解

P3159 [CQOI2012]交换棋子

题意：

把这题作为费用流入门题真的会自闭

有误请指出，谢谢~
正解： 首先可以把白棋当作空白区域，从起始位置到最终位置可以看成是若干黑色棋子的移动，并且每个格子有访问次数限制。可以把限制作为流量，每次的交换形似花费，这时候就能想到要用费用流了 。

首先考虑不拆点的做法，把棋盘每相邻的两个建立一条边，但是这样的话每个格子的访问次数限制就没法体现了，没有办法统计从四面八方经过的黑色棋子。

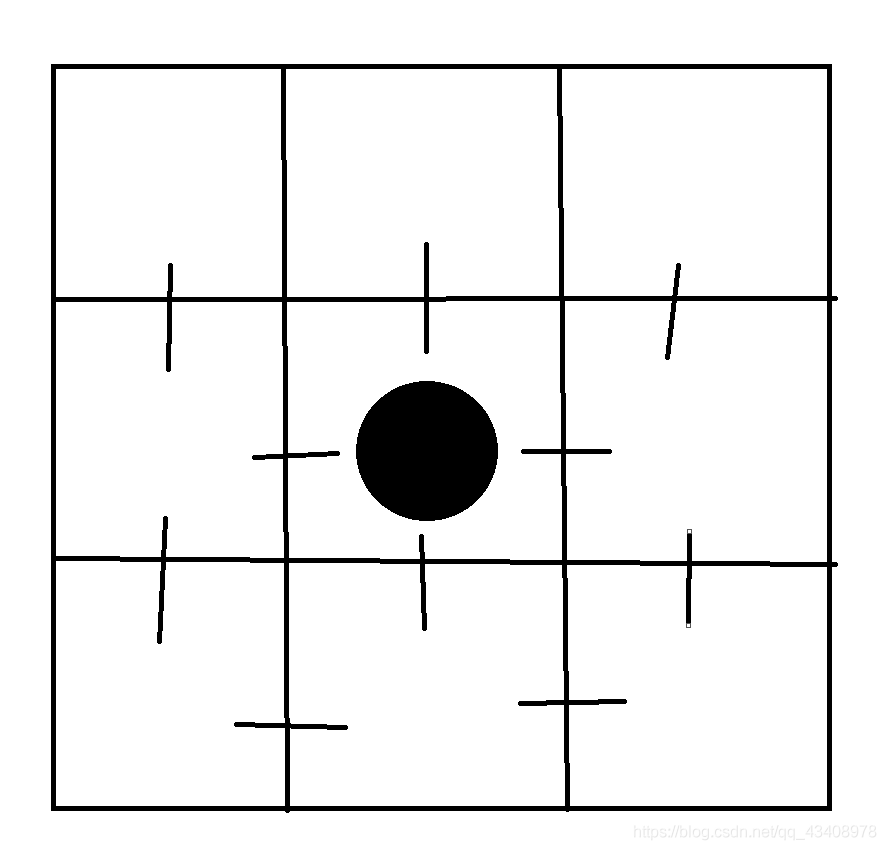
这时候考虑拆成两个点的做法。可以想到，除了起点和终点每次经过是访问一次，路径上的点访问次数都是两次。这样做确实也没问题，就是把每个点的流量设置为每个格子的限制，黑棋的起点和终点花费设置为1，其他的点设为2。

更好理解的做法是拆成三个点，访问次数限制转化为流量的时候三个点中的两条边均摊流量，花费是0，针对连到两个格子间的边流量设为无穷大，花费为1，最后算在这样的流量限制下能跑到的最小花费。具体细节看代码：

#include
#define fio ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define lson rt<<1, l, mid
#define rson rt<<1|1, mid+1, r
#define PI acos(-1)
#define eps 1e-8
#define rint register int
#define oo 1e5
using namespace std;
typedef long long LL;
typedef pair<LL, int> pli;
typedef pair<int, int> pii;
typedef pair<double, int> pdi;
typedef pair<LL, LL> pll;
typedef pair<double, double> pdd;
typedef map<char, int> mci;
typedef map<string, int> msi;
template<class T>
void read(T &res) {
  int f = 1; res = 0;
  char c = getchar();
  while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
  while(c >= '0' && c <= '9') { res = res * 10 + c - '0'; c = getchar(); }
  res *= f;
}
const int ne[8][2] = {1, 0, -1, 0, 0, 1, 0, -1, -1, -1, -1, 1, 1, -1, 1, 1};
const int INF = 0x7ffffff;
const int N = 1e6+10;
const LL Mod = 1e9+7;
const int M = 30;
struct xx {
  int next, to, flow, cost;
}e[N];
int tot = 1, head[N];
//起点，终点，流量，花费
void Add(int u, int v, int flow, int cost) {
  e[++tot] = xx {head[u], v, flow, cost};
  head[u] = tot;

  e[++tot] = xx {head[v], u, 0, -cost};
  head[v] = tot;
}
int n, m, s, t;
int dis[N], incf[N], vis[N], pre[N];
queue<int> q;
inline bool spfa() {
  for(int i = 0; i < N; ++i) dis[i] = INF, vis[i] = pre[i] = 0;
  dis[s] = 0; vis[s] = 1; incf[s] = INF;
  while(!q.empty()) q.pop();
  q.push(s);
  int u, v;
  while(!q.empty()) {
    u = q.front(); q.pop();
    vis[u] = 0;
    for(int i = head[u]; i; i = e[i].next) {
      v = e[i].to;
      if(e[i].flow && dis[v] > dis[u] + e[i].cost) {
        dis[v] = dis[u] + e[i].cost;
        incf[v] = min(incf[u], e[i].flow);
        pre[v] = i;
        if(!vis[v]) vis[v] = 1, q.push(v);
      }
    }
  }
  return dis[t] != INF;
}
int maxflow, mincost;
void MCMF() {
  while(spfa()) {
    maxflow += incf[t]; mincost += dis[t] * incf[t];
    for(int i = t; i != s; i = e[pre[i]^1].to) {
      e[pre[i]].flow -= incf[t], e[pre[i]^1].flow += incf[t];
    }
  }
}
int getp(int k, int x, int y) { return n*m*k + (x-1)*m + y; }
int tu1[M][M], tu2[M][M];
int main() {
  scanf("%d%d", &n, &m);
  s = 0; t = n * m * 3 + 1;
  char x;
  int cnt1 = 0, cnt2 = 0;
  
  for(int i = 1; i <= n; ++i) {
    for(int j = 1; j <= m; ++j) {
      cin >> x; tu1[i][j] = x - '0';
      //建立源点和黑色棋子起点中间点的边
      if(tu1[i][j]) ++cnt1, Add(s, getp(1, i, j), 1, 0);
    }
  }
  for(int i = 1; i <= n; ++i) {
    for(int j = 1; j <= m; ++j) {
      cin >> x; tu2[i][j] = x - '0';
      //建立黑色棋子终点中间点和汇点的边
      if(tu2[i][j]) ++cnt2, Add(getp(1, i, j), t, 1, 0);
    }
  }
  
  for(int i = 1, xx; i <= n; ++i) {
    for(int j = 1; j <= m; ++j) {
      cin >> x; xx = x - '0';
      //拆点！左边到中间再到右边
      if(tu1[i][j] == tu2[i][j]) {
        Add(getp(0, i, j), getp(1, i, j), xx/2, 0);
        Add(getp(1, i, j), getp(2, i, j), xx/2, 0);
      } else if(tu1[i][j]) {
        Add(getp(0, i, j), getp(1, i, j), xx/2, 0);
        Add(getp(1, i, j), getp(2, i, j), (xx+1)/2, 0);
      } else {
        Add(getp(0, i, j), getp(1, i, j), (xx+1)/2, 0);
        Add(getp(1, i, j), getp(2, i, j), xx/2, 0);
      }
    }
  }
  if(cnt1 != cnt2)  return puts("-1");

  for(int i = 1, ti, tj; i <= n; ++i) {
    for(int j = 1; j <= m; ++j) {
      for(int k = 0; k < 8; ++k) {
        ti = i + ne[k][0]; tj = j + ne[k][1];
        if(ti < 1 || tj < 1 || ti > n || tj > m) continue;
        //相邻格子之间建立边
        Add(getp(2, i, j), getp(0, ti, tj), INF, 1);
      }
    }
  }
  MCMF();
  printf("%d\n", maxflow == cnt2 ? mincost : -1);
  return 0;
}