机器学习分类问题中性能度量的方法

机器学习分类问题性能度量的方法

–date 2019.8.29
码完F1度量，ROC、AUC待天填坑
–date 2019.9.3
码完ROC、AUC，更换标题，代价曲线待天填坑
–date 2019.9.4
码完代价曲线，本博文完结

性能度量的目的

对于训练出来的学习器，我们最关注的还是它的泛化能力。即在训练样本外的学习能力，性能度量就是为了衡量泛化能力而诞生的。

性能度量的方法

最简单的：我们采用错误率进行统计，那么对于一般的回归问题，我们可以直接采用均方误差来统计
$$E(f;D)=\frac{1}{m}\sum _{i=1}^m(f(x_i)-y_i{)}^2$$
对于有概率密度的，均方误差可如此描述
$$E(f;D)={\int }_{x-D}(f(x)-y{)}^{2}p(x)dx$$
同时我们定义了精度与错误率。精度是：分类错误的样本数占样本总数的比例，精度则是分类正确的样本数占样本总数的比例，显然有：
$$\begin{gathered} P_{错}=\frac{n_{错}}{N_{样}} \\ {P}_{精}=1-P_{错} \end{gathered}$$
但是仅仅使用错误率与精度，并不能满足所有的任务需求，因为我们并不仅仅关注于整体的错误与正确率，我们还经常会考虑该分类在所有正例或者反例中的表现情况。所以我们提出了F1度量法

F1度量法

在了解F1度量法前我们首先需要知道的是查准率(precison)与查全率(recall)。我们拿二分类问题来说，那么其两者的定义为。

查准率指的做出了判断后，判断正确的准确率
$$P=\frac{TP}{TP+FP}$$
查全率指的是做出判断后，有多少正确的被囊括进来了
$$R=\frac{TP}{TP+FN}$$

查准率与查全率是一对矛盾的度量，虽然我们好像会认为可以通过加强学习器的能力来使得对于每一个样本得到准确的判断从而使得P=T=1，但是实际上当我们想要囊括进更多的正例的时候，R变高，调低阈值必然会使得判断不准确，P减小。

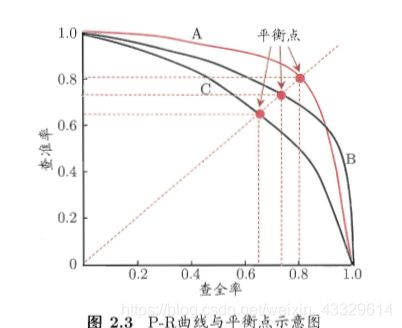
P值与R值在一定程度上都可以反映出该学习器的性能，所以显然的我们可以画出这样的一幅P-R图。

首先我们要注意的是P-R图在大多数情况下并非一条直线，并且不满足P+R=1这一关系。（如果想不明白继续参考定义）

P-R图直观的反映出了学习器在查全率与查准率上的表现，因此在比较不同的学习器的时候，我们可以有这样的直观比较方法：若曲线A完全位于B之上，那么A的查准率与查全率都同时在其之上，那么性能一定更优。比如此处的A、C，而两者有交叉则得视情况而定，如此处A、B。

P-R图还有一点需要注意的地方，我们将其称为平衡点（Break-Event Point），即为PR相等点。我们可以做出BEP直线来得到该学习器的BEP点。在PR图上，我们可以采用BEP度量，一般来说在采用BEP度量时，我们认为平衡点越高越好（因为这意味着PR越大），所以此时我们可以认为A优于B。

但BEP也还是太简单了，所以最常用的是我们真正的主角——F1度量

F1度量的具体形式

F1度量是基于查准率P与查全率R的调和平均值，对于每一组PR值我们都可以得出这样的一个F1的值

F1定义式：
$$\frac{1}{F1}=\frac{1}{2}\cdot (\frac{1}{P}+\frac{1}{R})$$
F1化简式：
$$F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{样例总数+TP-TN}$$
使用调和平均的原因：与算术平均与几何平均相比，调和平均更注重较小值。由于一般来说，我们都希望precision和recall同时高，所以要使用调和平均，来同时衡量二者的高低和均衡度这两个指标，从而避免在使用算术平均时，出现由于其中一个很高，另一个较低，造成的均值虚高的现象。

再对于具体问题，我们会分别提高P或者R，那么在性能度量时要加强/减弱这方面的度量，所以我们讲调和平均改称为加权调和平均，我们称其为F1度量的一般形式——Fβ。
$$F\beta =\frac{(1+{\beta }^2)\times P\times R}{({\beta }^2)\times P+R}$$
其中β>0度量了P对R的相对重要性，β=1的时候为标准的F1，β>1的时候更加注重P，β<1更加注重R。

在更多的时候我们会有很多二分类混淆矩阵，当我们希望在n个二分类混淆矩阵上综合考察PR时，我们又有两种做法，第一个是利用n组混淆矩阵算出n个P-R值，然后用平均值得到宏查准率(macro-P),宏查全率(macro-R)然后再计算宏F1(macro-F1)
$$\begin{gathered} macro-P=\frac{1}{n}\sum _{i=1}^n{P}_i \\ macro-R=\frac{1}{n}\sum _{i=1}^n{R}_i \\ macro-F1=\frac{2\times macro-P\times macro-R}{macro-P+macro-R} \end{gathered}$$
亦或者是对每一个TP FP TN FN计算平均值，再基于这些平均值利用定义算出微查准率(micro-P),微查全率(micro-R)然后再计算微F1(micro-F1)
$$\begin{gathered} micro-P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}} \\ micro-R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}} \\ micro-F1=\frac{2\times micro-P\times micro-R}{micro-P+micro-R} \end{gathered}$$

ROC与AUC

讲完了这些我们再来说另外一种度量方法：受试者工作特征(Receiver Operating Characteristiv)。它是用于反应TPR与FPR关系的一种曲线。在最开始的时候是用于雷达敌机检测的一种分析技术（即使是现在也还是会有ROC的压轴题…），在二十世纪六七十年代开始被用于心理学与医学的检测中（惭愧，最开始看AUC是看医学博文看懂的）。而现在被用于最新的机器学习中。

首先我们先来简单分析一下我们分类问题的基本方法，我们通过自己的算法（学习机）对一个样例进行检测得到一个实值或者概率预测，然后再将其与一个分类阈（yu）值进行比较，若大于阈值则分为正类，而小于则分为反类，我们也可以称这个阈值为截断点。

一般来说，神经网络会将这些值映射到**[0,1]**的空间中。简单的例子：我们摘取一个西瓜的特征进行评分，然后将阈值设为0.5，那么高于0.5的西瓜我们就会称其为“好瓜”。当然在不同的任务中，我们可以就P、R的不同侧重方向对阈值进行调整。

那么接下来再说一下TPR（真正例率）与FPR（假正例率）
$$\begin{gathered} TPR=\frac{TP}{TP+FN}=\frac{预测正例中的真正例}{所有正例} \\ FPR=\frac{FP}{TN+FP}=\frac{预测正例中的假正例}{所有反例} \end{gathered}$$
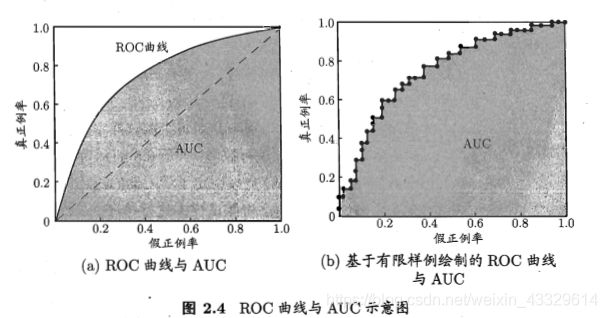
ROC图像就是描述TPR与FPR关系的图像。

对于每一个阈值，我们都可以得到不同的TPR与FPR，显然，当我们把阈值调的很高的时候，那么将不会有正例被预测为正例，TP=0，此时TPR=0，同理FP=0，FPR=0。而当阈值为0时，此时所有样例都会被预测为正例，所以此时TPR=FPR=1。那么首先我们可以得出ROC图像会经过（0,0），（1,1）两个定点，那么ROC图像究竟该是怎么样的呢？

我们知道ROC图像是由无数的TPR与FPR点对组成的，而实际上每个点还对应了一个阈值。而我们经过分析得到，从(0,0)到(1,1)是一个阈值减小的过程。而随着阈值的减小，TP与FP都必然增加（当超过阈值时判断为正例），所以显然它是一条从坐下到右上的图像，那为什么一般来说是曲线呢？这其实又和AUC有关。

AUC

AUC指的是ROC图像所围成的面积（Area Under Curve）。显然我们知道ROC图像所围成的面积是在[0,1]之间的。

我们先来看看AUC会不会存在为1的情况。显然，当AUC=1时我们有
$$\begin{gathered} AUC=1 \\ TPR=1 \end{gathered}$$
这意味着什么呢？意味着我们的模型在任意情况都不会漏掉任何一个正例，准确度为100%，当然显然是不可能的。

那么对于AUC=0的情况
$$\begin{gathered} AUC=0 \\ TPR=0 \end{gathered}$$
显然这也不可能，因为没有哪个阈值正常的模型可以100%过滤掉正例，因为这是另外一种意义上的完全精确。

我们再来看看这样的一种判断方法，我们称其为硬币判断法，对于任何一个样例我通过掷硬币来决定它是否为正例。那这样的话我们的ROC图像是不是就为一条从（0,0）到（1,1）的直线呢？此时AUC=0.5

因此我们可以知道，对于ROC图像来说，AUC实际上代表的是这个模型的精确度，只有当AUC>0.5的时候它才配称为一个模型，不然和掷硬币将没有区别。而当AUC>0.5的时候，ROC又得满足单调上升这个特性，这时就使得我们的图像变成一条向上凸的曲线啦！

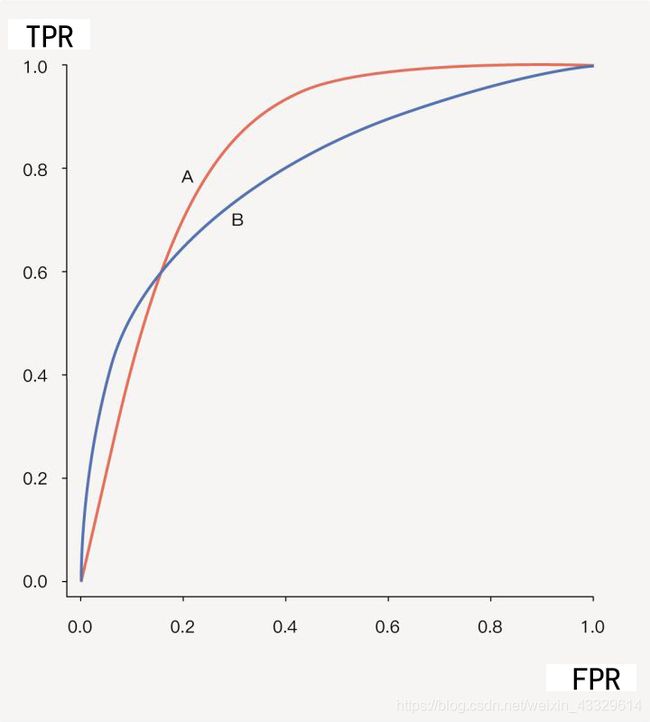
相交的ROC图像

在这张图中AUC-A=0.85，AUC-B=0.80，但是的话我们可以看出，B在某些时候的表现会优于A，此时就需要额外讨论

拓展：TPR亦被称为灵敏度。

代价曲线

ROC曲线实际上还是有自己的不足，因为在现实生活中，我们在进行判别的时候，不同的错误判断造成的代价是不同的。如将健康的人诊断为有病大不了会增加进步检查，而将有病的诊断为无病可能就会造成生命影响。

我们仍然使用最基本的二分类举例。

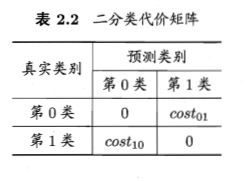
接下来的所有都默认0为反例，1为正例

我们将cost_ij记为将i类分成j类的代价

对于我们的ROC图像来说来说我们显然默认了cost₀₁=cost₁₀。因此ROC图像并不能很好地反映出学习器的期望总体代价，即犯错的代价，我们当然希望这个代价它越小越好，这也是反应机器学习性能的指标。

在学习代价曲线之前，我们首先确定我们代价曲线的目的：为了反应一个模型的期望代价的变化情况，从而反映出性能高低。

条件概率

为了方便接下来的描述，在正式走入代价曲线前，我们先来说一说条件概率这一个东西。

Pr[decide Hi|Hj]指的是条件概率，指的是在Hi已经发生的条件下Hj发生的概率。Pr[Hj]指的是先验概率，简单理解成Hj发生的概率。

我们拿**Pr[decide H1|H1]**举例，这里的意思就是在样例本身就是正例的情况下，被学习器判断成正例的概率。那么我们同理可以给出如下四种概率。

期望代价

我们据此给出期望代价的公式
$$E[cost]=(cos{t}_{01}\times P\times FNR)+(cos{t}_{10}\times (1-P)\times FPR)$$
为了便于对这个公式的理解，我们先在两个括号前分别乘以样例的总数N。

$$E[cost]=(cos{t}_{01}\times P\times FNR)\times N+(cos{t}_{10}\times (1-P)\times FPR)\times N$$
特地指出：这里的P指的是正例率(positive rate)，而不是查准率(precision)
$$P=\frac{TP+FN}{N_{总}}$$

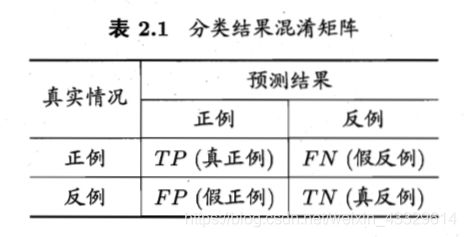
接下来我们对E[cost] 进行分析：所有的误差实际上只来自于两种，就是假正例与假反例，因为这才是认错的情况。

前半个括号：P×N是所有的正例，P×N×FNP就是所有的假反例了，乘以cost₀₁就是所有假反例的cost。

后半个括号：同理，是假正例的cost

在我们E[cost]的式子中，我们对其乘以了N便于理解，但我们发现实际上有无N，对E[cost]大小的反应是没有影响的。或者说：不乘以N，E[cost]反应的是概率代价。

那么我们顺便给出有n类的分类中期望代价的公式
$$E[cost]=\sum _{i=1}^n\sum _{j=1}^{n}cos{t}_{ij}Pr[decide{H}_i|H_j]Pr[H_j]$$

E[cost]-P图像

对于二分类问题的期望代价来说
$$E[cost]=(cos{t}_{01}\times P\times FNR)+(cos{t}_{10}\times (1-P)\times FPR)$$
很明显它是一个关于P的函数表达式，我们来看看它的取值：

显然，当P=0的时候，此时没有正例，所以此时E[cost]只会由FPR产生。
$$E[cost]=cos{t}_{10}\times FPR$$
同理当P=1的时候将会没有反例
$$E[cost]=cos{t}_{01}\times FNR$$
那么当cost_ij确定的时候，显然E-P图像为一条直线

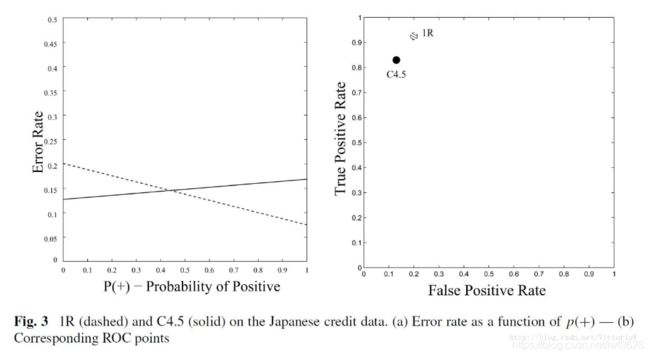
从代价曲线中，我们可以很容易地看出什么条件下那个分类器更好。以下就是一个例子：在交点的左侧，就是C4.5好，右侧则1R好。

归一化代价与其图像

首先我们来了解以下什么是归一化：归一化是一种简化计算的方式，即将有量纲的表达式，经过变换，化为无量纲的表达式，成为标量。 在多种计算中都经常用到这种方法。

意思就是说归一化是一种在不改变表达式相对大小的前提下进行映射的方式。而在这里我们想到：对于E[cost]来说，我们是不是可以找到一个理论上的最大 maxE[cost] 值，然后我们对于每一个E[cost]用其除以maxE[cost]得到我们的归一化E[cost]
$$Norm(E[cost])=\frac{E[cost]}{maxE[cost]}$$
显然最大的期望在所所有实例都被错误分类（即所有正类都被判别为负，所有负类都被判别为正类，此时FNR=1，FPR=1）的情况下出现，有：
$$maxE[cost]=P\times cos{t}_{01}+(1-P)\times cos{t}_{10}$$
则有：
$$Norm(E[cost])=\frac{E[cost]}{maxE[cost]}=\frac{cos{t}_{01}\times P\times FNR+cos{t}_{10}\times (1-P)\times FPR}{P\times cos{t}_{01}+(1-P)\times cos{t}_{10}}$$
显然我们可以通过这种方式将我们的E[cost]全部归一化到 [0,1] 空间内，且相对大小不发生改变。

但是这里有个问题：那就是我们的Norm(E[cost])-P不再是一条直线了，那么该怎么办呢？

其实没事，因为我们一开始说了代价曲线的目的是 为了反应一个模型的期望代价的变化情况，从而反映出性能高低。 所以大不了换呗，换成更方便直观的。

我们选择正例代价，PC。即为正例中所付出的代价。
$$\begin{gathered} PC=P\times C_{01} \\ maxPC=P\times C_{01}+（1-P）\times C_{10} \\ Norm(PC)=\frac{P\times C_{01}}{P\times C_{01}+（1-P）\times C_{10}} \end{gathered}$$
我们可以得到:
$$Norm(E[cost])=FNR\times Norm(PC)+FPR\times (1-Norm(PC))$$

因此，以Norm(PC)（归一化正例概率代价）为x轴，Norm(E[cost])(归一化代价)作为y轴得到的仍然是一条直线，并且对应的是一个分类器对应的代价曲线。

最终的曲线与面积的意义

最后的最后，我们再来回顾一下ROC，它反映的仅仅只是TPR与FPR的关系，而它是由无数的TPR-FPR点对组成的，而他们又分别对应了一个阈值。

而对于每一个阈值来说，我们得到的结果都是不一样的，期望代价也都是不一样的，我们可以认为它们彼此是一个个独立的分类器。因此我们将可以在一个Norm(E[cost])-P图像上做出这个学习器的所有Norm(E[cost])线段，而这样的话，它们必然彼此间会有交集，就像这样：


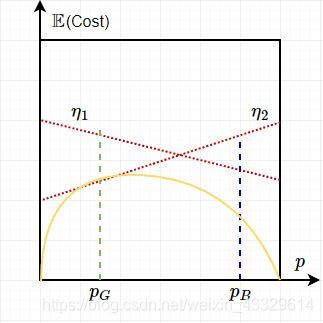
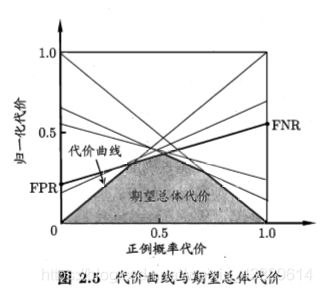
而我们需要的是这个模型的最小期望代价。对于不同的阈值η₁与η_2。在P_G这里，η₁的效果就没有η₂好，因此我们选择η₂。我们有许多许多的η，因此我们将它们全部画出来，面积会越围越小（可以自己想想为什么）。这样的话我们就绘制出了这样一条代价曲线,对应的是所有的可能性中那最小的代价期望。

那么我们的代价曲线所围成的面积是什么呢？其实也很简单，是这个学习器的期望代价，（注意不是分类器，因为一个阈值代表一个分类器），而面积的大小反应的就是该学习器的性能，显然面积越小性能越高，反之则反！

最后以我数学老师的一句话结尾：
不要小瞧了所有执迷不悟的人们，因为他们总有一天会顿悟！