LeetCode题解-接雨水Python实现

个人微信公众号：AI研习图书馆，欢迎关注~

深度学习知识及资源分享，学习交流，共同进步~

一、题目描述

42题：接雨水
难度：困难

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

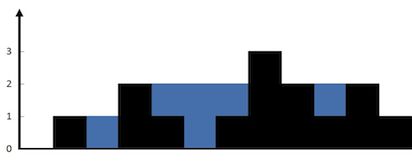
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

二、题解实现

1. 方法一-暴力求解

1.1 解题思路

一开始拿到题目之后可能会有些手足无措，我们从最原始的暴力解法开始思考，对于每个下标 i，我们计算它上方可以接多少雨水，然后将所有下标上的雨水加起来即可。

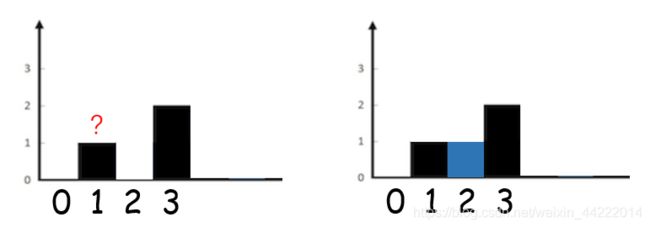
具体来说，如图我们假设输入为 [0,1,0,2]，凭感觉，我们得到接完雨水后的结果如右图。可以看到，只有下标 2 的上方可以接到雨水，其他地方的水会向两边“流掉”，所以无法接到水。

为什么是这样呢？首先看下标 1 ，它左边最高的柱子是下标 0 ，右边最高的柱子是下标 3 ，因为这两个柱子的较小值比下标 1 要低，所以下标 1 的上方没有水。相反，我们看下标 2，它左边最高的柱子是下标 1 ，右边最高的柱子是下标 3 ，这两个柱子较矮的是下标 1 ，它比下标 2 本身要高，所以下标 2 可以接到水，接的水就是高度差。

因此，我们遍历每个下标，寻找它左边和右边最高的柱子，判断是否可以接到水，将可接水的结果累加即可。

1.2 代码实现

class Solution:
    def trap(self, height: List[int]) -> int:
        ans = 0
        for i in range(len(height)):
            max_left, max_right = 0,0
            # 寻找 max_left
            for j in range(0,i):
                max_left = max(max_left,height[j])
            # 寻找 max_right
            for j in range(i,len(height)):
                max_right = max(max_right,height[j])
            if min(max_left,max_right) > height[i]:
                ans += min(max_left,max_right) - height[i]
        
        return ans

1.3 复杂度分析

时间复杂度：O(N^2)。最坏情况下，我们对于每个下标，都要向左和向右遍历直到两端，复杂度是 N 的平方。
空间复杂度：O(1)。使用了有限的 n, ans, maxleft, maxright。

2. 方法二-动态规划

2.1 解题思路

我们发现在寻找每个下标的左边和右边最高的柱子时，会对柱子进行反复搜索导致复杂度降低，假如我们使用两个数组 maxleft 和 maxright，maxleft[i] 表示下标 i 左边最高柱子的高度,maxright[i] 表示下标 i 右边最高柱子的高度，很明显，我们只需要一趟遍历就可以得到结果。这样由于避免了重复计算，时间复杂度会降低到 O(N)。

2.2 代码实现

class Solution:
    def trap(self, height: List[int]) -> int:
        # 边界条件
        if not height: return 0
        n = len(height)
        maxleft = [0] * n
        maxright = [0] * n
        ans = 0
        # 初始化
        maxleft[0] = height[0]
        maxright[n-1] = height[n-1]
        # 设置备忘录，分别存储左边和右边最高的柱子高度
        for i in range(1,n):
            maxleft[i] = max(height[i],maxleft[i-1])
        for j in range(n-2,-1,-1):
            maxright[j] = max(height[j],maxright[j+1])
        # 一趟遍历，比较每个位置可以存储多少水
        for i in range(n):
            if min(maxleft[i],maxright[i]) > height[i]:
                ans += min(maxleft[i],maxright[i]) - height[i]
        return ans

2.3 复杂度分析

由于使用了数组，我们的空间复杂度会增加到 O(N),如何能把空间复杂度也降低呢？我们可以使用双指针法。

3. 方法三-双指针法

3.1 解题思路

双指针法就是将上边的一个下标 i，变为两个下标 left，right，分别位于输入数组的两端。向中间移动时，边移动边计算。

除此之外，我们使用 maxleft 作为 0…left 的最大值，maxright 作为 right…结尾 的最大值。代码看不懂的地方可以看幻灯片帮助理解~

完整幻灯片，请移步网页——>幻灯片网页
该网页还有题解全部过程~

3.2 代码实现

class Solution:
    def trap(self, height: List[int]) -> int:
        # 边界条件
        if not height: return 0
        n = len(height)

        left,right = 0, n - 1  # 分别位于输入数组的两端
        maxleft,maxright = height[0],height[n - 1]
        ans = 0

        while left <= right:
            maxleft = max(height[left],maxleft)
            maxright = max(height[right],maxright)
            if maxleft < maxright:
                ans += maxleft - height[left]
                left += 1
            else:
                ans += maxright - height[right]
                right -= 1

        return ans

3.3 复杂度分析

• 时间复杂度：O(N)。遍历了一遍数组。
• 空间复杂度：O(1)。使用了有限的 left, right, ans,
  maxleft, maxright。

三、实验结果

如有疑问，欢迎批评指正~

码字不易，欢迎点赞，关注~~~

您的支持，是我不断创作的最大动力~

欢迎点赞，关注，留言交流~

深度学习，乐此不疲~