C语言日常练习（一）

C语言日常练习

第一天

1、杨辉三角

void Fun(int n);
int a[100][100];
int main(void)
{
	printf("\n\n");

	int n;
	printf("请输入杨辉三角行数\n");
	scanf("%d", &n);
	printf("\n\n");
	Fun(n);

	printf("\n\n");
	system("pause");
	return 0;
}

void Fun(int n)
{
	for (int i = 0; i < n; i++)
	{
		a[i][0] = 1;	//每行首元素为1
		a[i][i] = 1;	//每行末元素为1
	}
	
	for (int i = 2; i < n; i++)		//前两行不用计算				
	{
		for (int j = 1; j <= i - 1; j++)
		{
			a[i][j] = a[i - 1][j] + a[i-1][j - 1];	//当前元素等于上行同位置元素与上行前一个元素之和
			
		}
	}
	for (int i = 0; i < n; i++)		//打印
	{
		for (int j = 0; j <= i; j++)
		{
			printf("%4d ", a[i][j]);
		}
		printf("\n");
	}
	
}

运行测试：

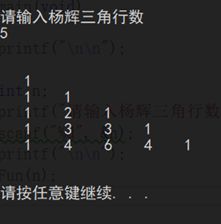
2、将整型数组中的所有元素镜像对调，第一个与最后一个对调，第二个与倒数第二个对调，按对调后的结果输出。

void Fun(int k[], int num);


int main(void)
{
	printf("\n\n");
	int a[10] = { 3,6,9,0,2,5,8,1,4,7 };

	for (int i = 0; i < 10; i++)
		printf("%d", a[i]);
	printf("\n");

	Fun(a, 10);

	for (int i = 0; i < 10; i++)
		printf("%d", a[i]);
	printf("\n");
	system("pause");
	return 0;
}

void Fun(int k[], int num)
{
	int i, j, temp = 0;		//循环控制变量 i j ,临时变量temp
	for (i = 0; i < num/2; i++)	//注：只能循环一半，否则对调后又会被对调回来		
	{										
		for (j = num - 1; j > num/2; j--)
		{
			if (i + j == num - 1)	//镜像元素下标之和为：数组长度-1
			{
				temp = k[i];
				k[i] = k[j];
				k[j] = temp;
				break;
			}
		}
	}
}

运行测试：

3、二位数组行列元素互换（转置矩阵）

int main(void)
{
	printf("\n\n");

	int A[100][100], B[100][100];
	int a, b;
	printf("请输入矩阵行列\n");
	scanf("%d%d", &a, &b);
	printf("请输入矩阵\n");
	for (int i = 0; i < a; i++)
	{
		for (int j = 0; j < b; j++)
		{
			scanf("%d", &A[i][j]);
			B[j][i] = A[i][j];	//将A中元素赋值给B数组中的对应位置
		}
		
	}

	printf("\n\n");
	for (int i = 0; i < b; i++)
	{
		for (int j = 0; j < a; j++)
		{
			printf("%4d ", B[i][j]);
		}
		printf("\n");
	}

	printf("\n\n");
	system("pause");
	return 0;
}

运行测试：

4、矩阵乘法

思考：矩阵乘法并不难，在清楚原理之后，清晰的思路是解这道题的关键

int main(void)
{
	printf("\n\n");

	int a, b, m, n;		//控制两个矩阵规模
	int temp;			//临时变量
	int A[100][100], B[100][100],C[100][100];	//三个矩阵
	printf("请输入第一个矩阵的行、列：\n");
	scanf("%d%d", &a, &b);	
	printf("请输入第二个矩阵的行、列：\n");
	scanf("%d%d", &m, &n);
	while (b != m)
	{
		printf("\n矩阵规模不合法，请重输!\n\n");
		printf("请输入第一个矩阵的行、列：\n");
		scanf("%d%d", &a, &b);
		printf("请输入第二个矩阵的行、列：\n");
		scanf("%d%d", &m, &n);
	}
	printf("请输入第一个矩阵\n");
	for (int i = 0; i < a; i++)
	{
		for (int j = 0; j < b; j++)
			scanf("%d", &A[i][j]);
	}
	

	printf("请输入第二个矩阵\n");
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < n; j++)
			scanf("%d", &B[i][j]);
	}

	for (int i = 0; i < a; i++)    //“i==a”
	{	
		for (int j = 0; j < n; j++)    //“j==n”  “a==n”
		{	temp = 0;
			for (int h = 0; h < m; h++)    //“h==m==b”
			{
				temp += A[i][h] * B[h][j];		//用temp记录，相乘之积求和后再赋给C[i][j]
			}
			C[i][j] = temp;
		}
	}

	printf("\n\n相乘所得矩阵为\n");
	for (int i = 0; i < a; i++)
	{
		for (int j = 0; j < n; j++)
		{
			printf("%3d ", C[i][j]);
		}
		printf("\n");
	}


	printf("\n\n");
	system("pause");
	return 0;
}

运行测试：

5、古典问题：有一对兔子，从出生后第3个月起每个月都生一对兔子，小兔子长到第三个月后每个月又生一对兔子，假如兔子都不死，问每个月的兔子总数为多少？

思考：最经典的递归求斐波拉契数列

int Fun(int n);
int main(void)
{
	printf("\n\n");

	int n;
	printf("请输入月数\n");
	scanf("%d", &n);
	printf("情况如下\n");
	for(int i=1;i<=n;i++)
	printf("%d ", Fun(i));
	printf("\n\n此时共有%d只兔子", Fun(n));




	printf("\n\n");
	system("pause");
	return 0;
}

int Fun(int n)
{
	if (n == 1)
		return 1;
	else if (n == 2)
		return 1;
	else
		return Fun(n - 1) + Fun(n - 2);					//递归，前两项相加
}

运行测试：